Thread by @genkuroki

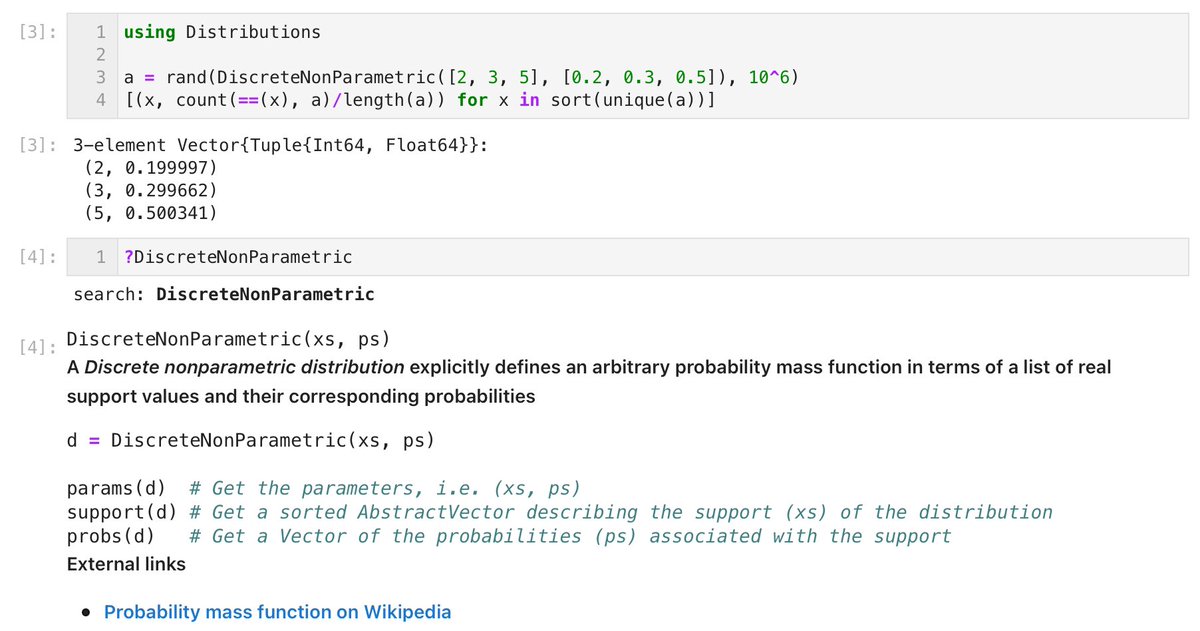
「もとにする数」？しかも小3で。

これはひどいな。

こんな問題については一生理解する必要はありません。

この手の算数プリントに気付くたびに、うちではお母さんが素早く子に「こんなの理解しなくていい！」とはっきり言う方針になっています。

https://twitter.com/hijiridesign/status/1439387093826891779

算数教育界は「どんな数をもとにするか」のような算数教育界でしか通用しない子供が習得し難い用語を算数教育界の都合で使用する傾向があります。

そういう非常識で子供に優しくない人たちに、子供の側が合わせてやる必要はないです。

「自分ちではマル❤️」でいいと思いました。

https://twitter.com/hijiridesign/status/1439599756695642115

#超算数 リンク先のような反応は頓珍漢。

実際、【どんな数をもとにすると】の意味がわからない、という大人側からの反応が続出している。

高等教育を受けた日本語話者であっても、その言い回しを理解できない。

国語的には【どんな数をもとにすると】という言い回しには教える価値がない。

https://twitter.com/szsk_edu/status/1439593745570168841

#超算数 以下のリンク先へのコメント

その通りです。「どんな数をもとにすると」という言い回しは非常識であり、通用しません。

算数教育界には伝統的に、大人でさえ理解できない言い回しを使って子供に算数を教えようとする非常識で無慈悲な傾向があります。

子供に優しくない大人になっちゃダメ。

https://twitter.com/d19920605/status/1439736152374661121

この反応、結構好き！優しい！

https://twitter.com/thunder5178/status/1439586348839542796

#超算数 これは特にひどい非常識で空瓶及使用済紙及腐敗食物的被廃棄物で狼藉之義也な反応。

【どんな数をもとにすると】という言い回しは日本語圏では通常使用されない。これが国語的な常識。

この手の国語的に非常識な先生には子供に国語を教えさせるべきではない。

https://twitter.com/syuchi1220/status/1439740868869558274

私も、国語的におかしな問題だと思いました。

これを擁護したくなる小学校の先生は自分自身の日本語に関する感覚が非常識なものになってしまっていることに気付くべきで、子供に非常識な感覚を押し付ける横暴を今後は絶対にしないと誓うべきだ。

https://twitter.com/Nagapiii/status/1439737017563181057

ほんとその通りで、日本語的に非常識。

子供に忖度させちゃダメですよね。

子供にわかりやすい言葉で優しく易しく教えることが小学校の先生の基本だと思うのですが、現実にはそうなっていないという大問題。

https://twitter.com/ray_fyk/status/1439645238549647360

#超算数 これも最低の反応

【どんな数をもとにすると】のような言い回しが日本語圏で普通ではなく、算数の内容を理解するためにも無用であることを何も理解していない。

わざわざ日本語的に非常識な子供にとって易しく(優しく)ない言い回しで算数を教えようとする行為はさすがにまずいだろう。

https://twitter.com/wacchiwacchi2/status/1439602939299971073

#超算数 ついでに述べておくが、算数の教科書で採用されている「4この2つ分」のような日本語的に非常識な言い回しで子供にかけ算を教える行為もやめるべきだ。

その言い回しを理解している小2と小3の子は5人に1人程度しかいない。

https://twitter.com/genkuroki/status/1435572459835576331

#超算数 大人が違和感を感じる子供が理解できない言い回しで算数を教えようとする行為は、算数教育界の伝統になってしまっている。

算数の教科書もそういう悪しき伝統に沿って執筆されている。

子供に優しくない連中がここまで堂々と偉そうにしている世界が他にあるだろうか？

子供には優しく！

#超算数 添付画像①②は

aue.repo.nii.ac.jp/index.php?acti…
小学校低学年児童の算数語彙力の調査研究
志水廣
2015

より。③は東京書籍小2算数教科書より。

「4この2つ分」の意味の正解率が突出して低いのに、教科書ではその言い回しが平気で使われている。

我々は社会全体でこういう行為を非難するべき。

算数の教科書が上で示したように

　子供が理解できない言い回しで算数を教えようとする

書き方になっているので、小学校の先生になるために特に重要な資質は

⭕️教科書にある子供にとってわかりにくい言い回しを避けて
　易しく分かりやすく教える能力

です。これの逆は非常にまずい。

古今東西、人間の心を無くした真の悪者は子供を虐待する輩として描かれていることが多いと思います。

算数を教えるときに、その手の悪者になることに躊躇しない人達が現実に大量に存在するのは驚くべきことです。

「ああ、これを言っちゃうと、自分は真の悪者になっちゃうな」と感じないのか？

この話題が盛り上がり易い理由は2つある。

* 普通の人には真の悪者が子供を虐待している問題のように見える。

* 真の悪者達はそのことに気付かずに子供に優しくない発言を何度でも堂々と繰り返す。

算数の教科書自体が子供に優しくない人達が執筆していそうだということはもっと有名になった方がよい。

ふみさんがツイートを削除してしまったようなので、投稿日時を含む完全なスクショを記録として残しておきます。

【大人もわかんないって単純に国語力無さすぎなのでは？】
　　　↑
これはひどい暴言！

#超算数

算数教育の研究によって、高学年児童は「もとにする量」「比べ(られ)る量」という用語を理解することに困難を覚えることが知られています。

科学者や技術者になるためにも無用な用語です。

だから、普通の人なら、リンク先のように

　それらの用語を使わずに工夫して教えよう

と考える。

https://twitter.com/genkuroki/status/479877103131713536

#超算数 で、「もとにする量」などの子供にとって易しくない日本語的にも非常識な用語を用いる教科書通りに教えるT群とそうではない工夫した教え方をするE群を比較したら、結果はE群の圧勝に終わった。

こういう授業実践の比較研究があります。

https://twitter.com/genkuroki/status/479877621686083585

#超算数 その研究結果を見た人は、「もとにする量」のような子供に優しくない用語を用いる教え方はやめた方がよいと、誰だって感じると思います。

しかし、算数教育界の伝統はそういうことを許しません。

現在の小5算数教科書も「もとにする量」という用語を使って教える方針が維持されています。

#超算数 このスレッドで問題になっている【どんな数をもとにすると】という小3での言い回しは、小5で割合を習うときの「もとにする量」という用語に繋がって行くのですが、その「もとにする量」という用語の使用自体が割合教育において有害であることが分かっているという話になっているのです。

#超算数 これもひどい。

私に直接リプライを送って来たことから危険回避能力も欠けている(笑)→添付画像①

②③は

note.com/kazuto0606/n/n…

より。④は「東京出版」ではなく東京書籍の算数の教科書の小3上より。

【どんな数をもとにすると】という言い回しを当然としていて子供に優しくない。

https://twitter.com/kazuto0606a/status/1439725176912973826

【34000は，1000を何こ集めた数ですか】が解けることと、【どんな数をもとにすると】という言い回しの解釈で忖度することは全然違うことです。

国語的に非常識で一生理解する必要がない言い回しで問題を出して、子供に忖度させようとすることが平気な人物は教育の世界から出て行くべきです。

#超算数 関連必読スレッド↓

https://twitter.com/temmusu_n/status/1439777028975202304

#超算数 これもひどい。

【どんな数をもとにすると】のような一生知らなくても困らない(割合概念の理解にも不要、科学者や技術者になるためならなおさら不要)な言い回しを使って算数の問題を出す行為は、国語的に非常識であることにしていない点は相当にひどい。

https://twitter.com/not_too_late/status/1439612841485430784

#超算数

個人的には、この問題を正解してしまっている場合の方が心配。

自分ちの子が、変なことを教える先生が言うことに忠実に従ってしまっている様子を発見してしまうことは恐怖そのものだ😱

不正解になっていたら、心底ホッとしてニコニコできる。

聖さんちの娘さんはラッキーだったかも！

https://twitter.com/hijiridesign/status/1439387093826891779

#超算数 かけ算順序問題の場合にも、仮に自分ちの子がかけ算順序で全部正解していて、その理由が

* 「ずつ」が出てくればかけ算の問題
* 「ずつ」のついている数はかけ算の式で先に書く

と信じていることだとしたら、それに気付いた保護者は真の恐怖と悲しみと怒りを感じることになるだろう。😭

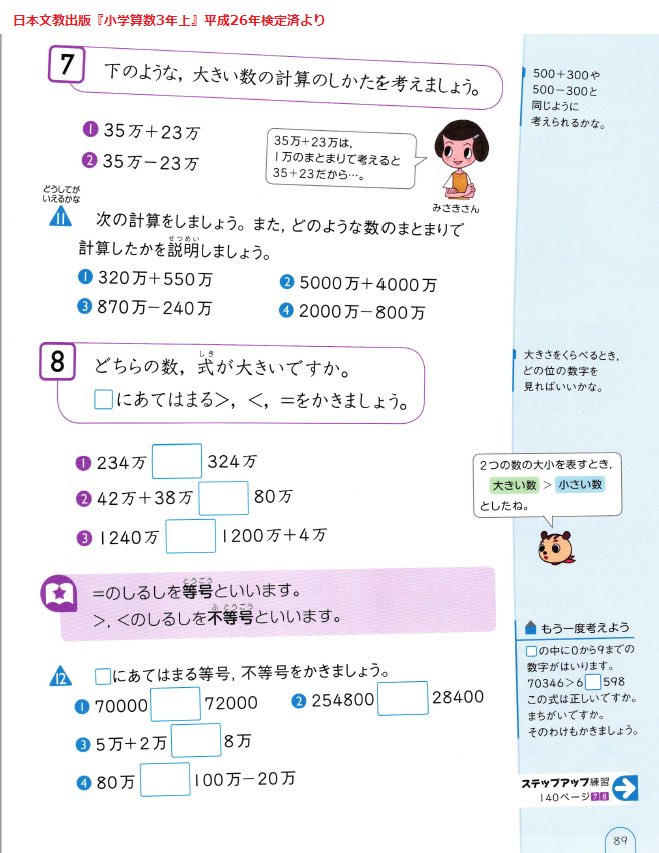
#超算数 手元にある小3の算数の教科書のデータの大きな数を扱う節の部分をチェックしてみました。

一生理解する必要がない「どんな数をもとにすると」という言い回しは発見できませんでした。

内容的に最も近いものを添付画像に引用。

「どんな数をもとにすると」とは相当に印象が違う感じ。

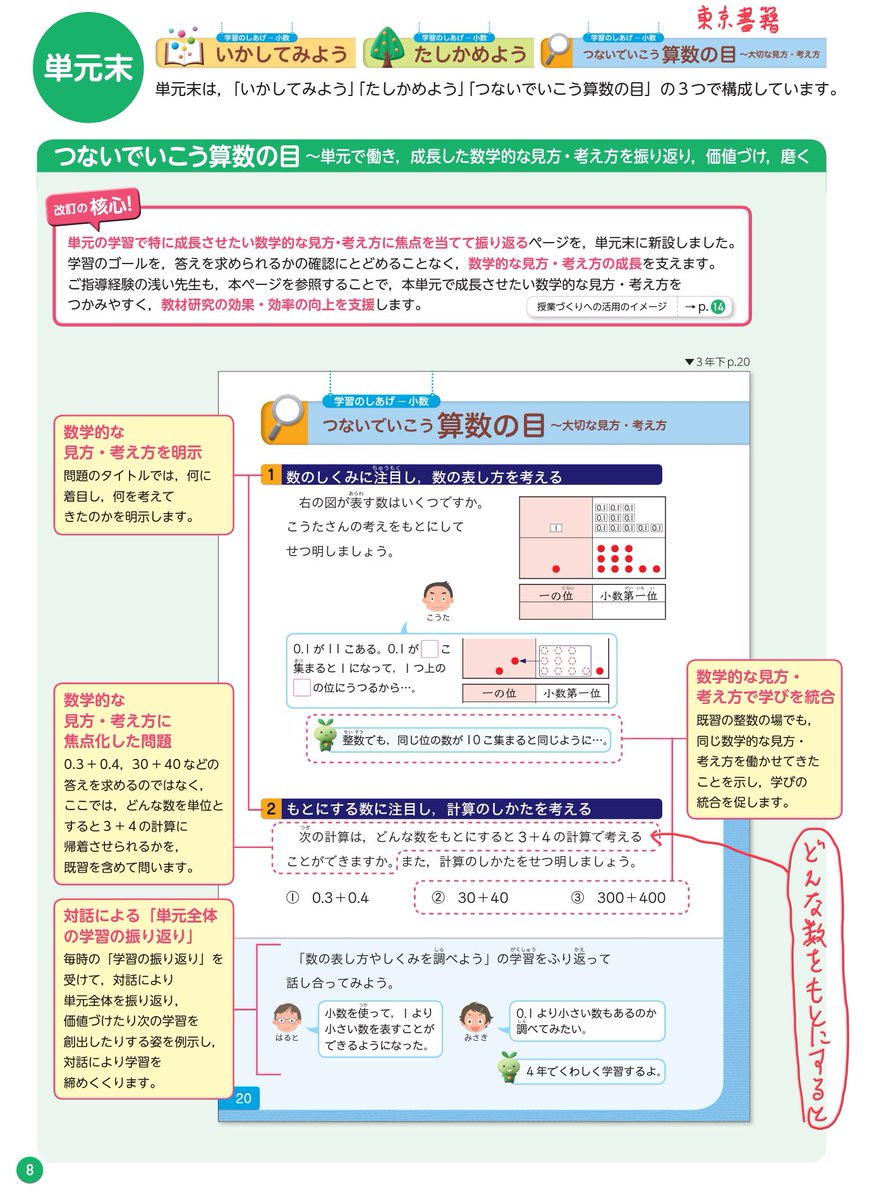
先程RTしたように、2020年の東京書籍の教科書には以下のような記述があるらしいです。これはひどいな。

子供にどう見えているかは、ページ丸ごとを見ないと十分に分からないので、ページ丸ごと見せてくれる人がいると助かります。

特に「もとにする数」の説明が東京書籍の小3上の算数教科書でどうなっているかを知りたい人は多いと思います。

小5算数教科書の割合の章には「もとにする量」「比べ(られ)る量」という用語が出てきます。そして、それらの用語の使用に児童が困難を覚えることが、算数教育の研究で知られています。

要するに小5での割合教育で一生理解する必要がなくて児童もよく理解できない悪名高い用語である「もとにする量」「比べ(られ)る量」を使うだけではなく、小3で「もとにする数」という用語を使い始めた。

どうしてこういう子供に優しくない教え方をしたがるのか？

資料追加

ten.tokyo-shoseki.co.jp/text/shou/sans…
東京書籍のパンフレット

より。添付画像②に

【どんな数をもとにすると3+4の計算で考えることができますか。～

① 0.3+0.4　　　② 30+40　　　③ 300+400】

と書いてあります。

どうしてわざわざ児童が困ることが前もって分かっている言い回しを使うのか？

どうしてわざわざ児童が困ることが前もって分かっている言い回しを使うのか？

算数教育界にそういう伝統があるから。

小2でのかけ算導入で使われている「4この2つ分」というフレーズの意味を理解している児童は5人に1人しかいないらしい。この言い回しを算数の教科書に導入した人は責任を取るべき。