Thread by @BTeseracto

Conforme te acercas a un agujero negro el tiempo empieza a dilatarse. Hasta el punto de que en el horizonte de sucesos parece congelarse. Si lleva un tiempo infinito atravesar este punto, y los agujeros negros viven un tiempo finito ¿Es realmente posible caer en uno de ellos?

A esta cuestión le hemos dado una cantidad preocupante de vueltas. No nos cabía duda de que algo se nos estaba escapando, pero no terminábamos de ver el qué. Vamos a explicar el problema con un poco de calma.

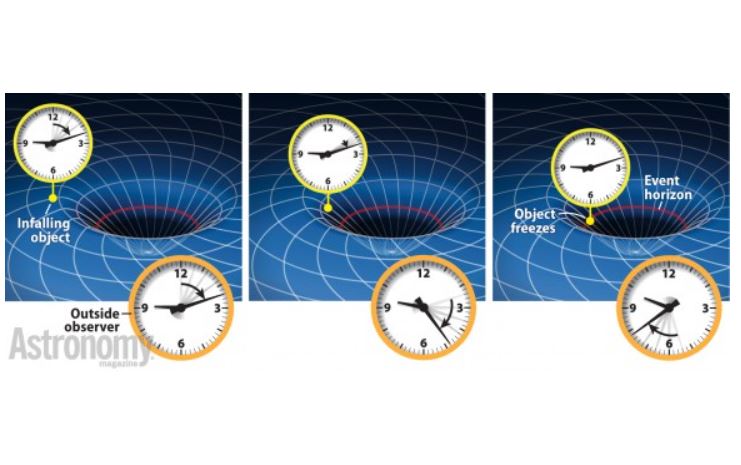
Imaginemos dos observadores. Uno en caída libre hacia el agujero negro y otro mirando desde la lejanía, ajeno a los efectos del agujero negro. Los hechos son los mismos, pero la percepción de cada uno de esta situación es radicalmente opuesta.

Empecemos por el caso más simple, el del observador en caída libre. Pongamos que el AN es lo bastante grande como para que se pueda atravesar el horizonte de sucesos sin problemas. Este observador lo atravesaría sin trabas y en un tiempo finito alcanzaría la singularidad.

El problema viene al preguntar al otro observador. Este relataría una historia completamente distinta, para él la nave e incluso el propio tripulante se movían cada más y más despacio, hasta congelarse en el tiempo.

O esto era lo que nosotros pensábamos en base a las divergencias en las métricas. Evidentemente algo no estábamos teniendo en cuenta.

No puede costar toda la eternidad caer en un agujero negro, en este caso nunca llegarían a crecer. Como nosotros no somos expertos en la materia nos vimos arrastrados a buscar información y a darle muchas vueltas, tal vez demasiadas.

Nuestra primera línea de búsqueda fueron las métricas, es decir, las soluciones para diferentes sistemas de la ecuación de Einstein en la relatividad general.

Supusimos que la métrica de Schwarzschild, que nos era más familiar, era poco realista pues describe el campo gravitatorio de una masa esférica y sin rotación. Es difícil imaginar un objeto tan compacto sin rotación, por una cuestión de conservación del momento angular.

Pensamos que la métrica que describe a los agujeros negros con rotación daría una solución al problema. Así que empezamos a estudiar la métrica de Kerr, mucho más complicada. Pero ni tuvimos éxito en entenderla bien ni nos sirvió para encontrar las respuestas que buscábamos.

Seguimos buscando hasta darnos cuenta de que la solución era más física que matemática. La respuesta estaba en la naturaleza del agujero negro. Porque, ¿qué es un agujero negro sino curvatura?

Pero antes volvamos a nuestros dos observadores. En nuestra descripción de la situación hemos dejado de lado algunos puntos importantes, al igual que los obviamos nosotros cuando empezamos a darle vueltas a este problema.

Un análisis superficial, como el que hacíamos nosotros, no estaba teniendo en cuenta otras diferencias en la percepción de ambos observadores a parte del tiempo. En concreto, el corrimiento al rojo.

Y es que conforme el intrépido astronauta se acerca al AN la luz que emite su nave y que permite a su compañero seguir su pista se desplaza hacia el rojo, lejos del espectro visible y en última instancia en un rango completamente indetectable.

Esto ya debería darnos una pista de lo que está ocurriendo, pero prosigamos. Supongamos que en lugar de observar a un astronauta caer, lo que hacemos es dejar caer una sonda que envía una señal por segundo.

Al principio registraría la señal con un pulso por segundo. Pero, a pesar de que en su tiempo propio la sonda continuaría emitiendo una señal cada segundo, poco a poco habría más tiempo entre señal y señal para el observador lejano.

Más y más tiempo hasta que la diferencia entre un pulso y el siguiente sería toda la eternidad. Se encontraría con que ya no se puede ver ni percibir, con lo que se podría preguntar ¿La sonda ha cruzado el horizonte de sucesos?

Vamos a irnos a un caso más extremo, uno que nos permita ver la situación con más claridad. Supongamos que un AN de digamos 5 masas solares se traga una estrella de 3.

La estrella se deforma y empieza a caer en espiral hacia el agujero negro. La luz que emite se va al infrarrojo hasta el punto de que resulta invisible, sin llegar a emitir ninguna otra clase de energía. ¿Cuál es el resultado?

Al agujero negro de 5 masas solares ahora se le suman otras 3 masas solares aisladas del universo exterior. Es decir, un agujero negro de 8 masas solares. De facto ha cruzado el horizonte porque ahora forma parte del agujero negro.

Los agujeros negros son espacio tiempo vacío, en última instancia curvatura. Y ambas curvaturas, las de la estrella y las del agujero negro original forman una nueva, más grande.

El observador que cae en el agujero negro añade su curvatura a la del agujero negro, con lo que pasa a ser parte de él, obteniendo así un viaje de ida hacia la singularidad, con dramáticos resultados para su esperanza de vida. Pero ese es otro tema.

Créditos de la primera imagen del hilo: astronomy magazinge (astronomy.com)