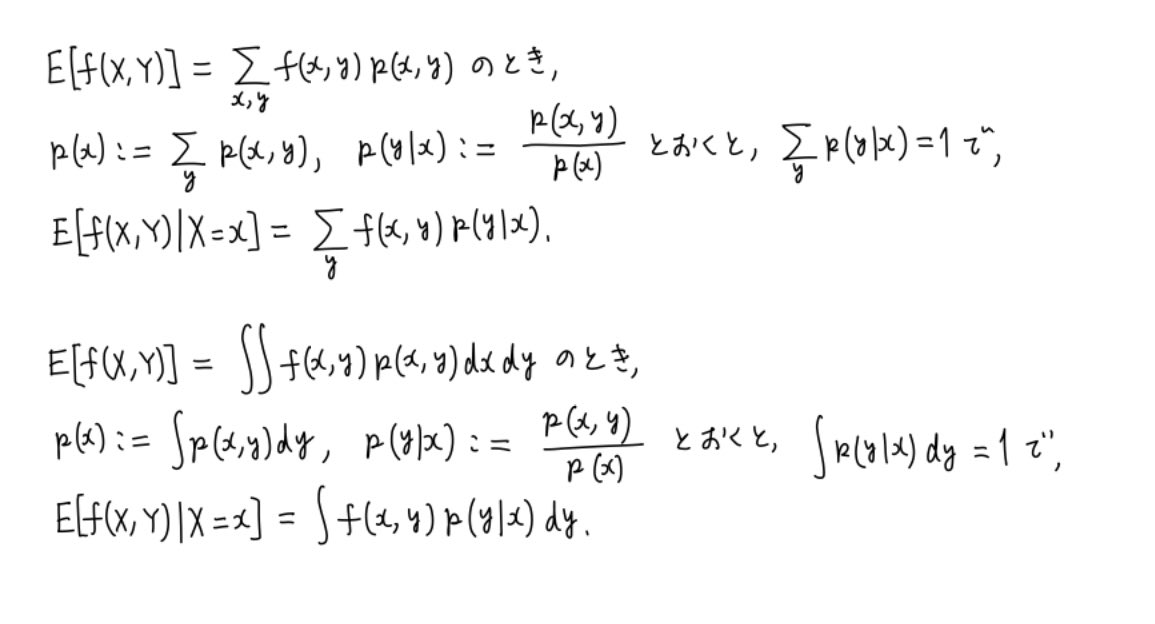#統計
改訂増補版:統計検定を理解せずに使っている人のために I
池田 郁男
東北大学未来科学技術共同研究センター
Published: 2019-08-01
© 2019 公益社団法人日本農芸化学会
katosei.jsbba.or.jp/view_html.php?…
いやあ、これは色々雑な解説の仕方で頭を抱えた。


改訂増補版:統計検定を理解せずに使っている人のために I
池田 郁男
東北大学未来科学技術共同研究センター
Published: 2019-08-01
© 2019 公益社団法人日本農芸化学会
katosei.jsbba.or.jp/view_html.php?…
いやあ、これは色々雑な解説の仕方で頭を抱えた。
https://twitter.com/shirakawa_love/status/1468167392362926088



#統計
改訂増補版:統計検定を理解せずに使っている人のためにII
池田 郁男
東北大学未来科学技術共同研究センター
Published: 2019-09-01
© 2019 公益社団法人日本農芸化学会
katosei.jsbba.or.jp/view_html.php?…
Welch検定で自由度を四捨五入するのはやめて!
以前にもこれ見た覚えがある。
改訂増補版:統計検定を理解せずに使っている人のためにII
池田 郁男
東北大学未来科学技術共同研究センター
Published: 2019-09-01
© 2019 公益社団法人日本農芸化学会
katosei.jsbba.or.jp/view_html.php?…
Welch検定で自由度を四捨五入するのはやめて!
以前にもこれ見た覚えがある。
https://twitter.com/shirakawa_love/status/1468167392362926088

#統計 不偏分散の平方根は母標準偏差の不偏推定量にならないことは自明。
多分それよりも要注意なのは、不偏分散は緩い条件のもとで任意のi.i.d.サンプルで母分散の不偏推定量になること。これは例外的なので要注意。
一般に不偏推定量は特定のモデル内でしか不偏推定量にならない。
多分それよりも要注意なのは、不偏分散は緩い条件のもとで任意のi.i.d.サンプルで母分散の不偏推定量になること。これは例外的なので要注意。
一般に不偏推定量は特定のモデル内でしか不偏推定量にならない。
https://twitter.com/shirakawa_love/status/1468168348337078283
#統計 自由度に関するこの説明も雑すぎ。たぶん、これを書いている人自身が理解していない。
線形代数の直交射影の直観があれば、直交射影先の部分空間の直交補空間の次元が添付画像の文脈での自由度になる。
katosei.jsbba.or.jp/view_html.php?…
線形代数の直交射影の直観があれば、直交射影先の部分空間の直交補空間の次元が添付画像の文脈での自由度になる。
katosei.jsbba.or.jp/view_html.php?…

#統計 正規分布モデルの統計学は、内積付き実⃗ベクトル空間の線形代数の微積分による書き直しになっていて、推定は部分空間への直交射影になり、その直交補空間がノイズ方向だと解釈される。
#統計 さらにややこしいことに、非常に沢山の種類がある最尤法の漸近論を基礎とするχ²検定で使うχ²分布の自由度の話もあります。
その意味での自由度は、モデルのパラメータ空間の次元が帰無仮説によって何次元下がるかを意味しています。
Wilksの定理が神。
その意味での自由度は、モデルのパラメータ空間の次元が帰無仮説によって何次元下がるかを意味しています。
Wilksの定理が神。
#統計 多分、理解せずに「はじき」のように統計学的道具を使っている集団があって、その使い方があまりにもひどい場合がある現状について、十分に理解していない人が改善する仕事を任されているという構造的な問題があるのだと思う。
#統計 教える側の理解度を高めることをサポートする社会的な仕組みが必要。人にお金を出さないと多分どうにもならない。
#統計 添付画像では標準偏差の不偏推定量を求めています。ただし、標準偏差のその不偏推定量は正規分布モデル内での不偏推定量にすぎません。
不偏分散が正規分布モデル以外でも普遍的に分散の不偏推定量になるのは非常に特殊な話になります。
不偏分散が正規分布モデル以外でも普遍的に分散の不偏推定量になるのは非常に特殊な話になります。
https://twitter.com/genkuroki/status/1468223622590640130

#統計 モデル内に現実のデータを生成している未知の分布が含まれていない場合には、そのモデル内での不偏推定量は現実には全然不偏推定量でなくなります。
推定量の不偏性は極めて強い条件であり、不偏推定法の中で最良のものを見つけても「井の中の蛙」になるかもしれません。
推定量の不偏性は極めて強い条件であり、不偏推定法の中で最良のものを見つけても「井の中の蛙」になるかもしれません。
#統計 σのその不偏推定量は正規分布モデル内部でのみ不偏になる推定量なので、正規分布モデル外でも普遍的に母分散の不偏推定量になる不偏分散とは頑健性が大幅に違うことに注意。
「モデル内のみ不偏推定量」の不偏性は現実の統計分析では大して意味がないと個人的には思う。
「モデル内のみ不偏推定量」の不偏性は現実の統計分析では大して意味がないと個人的には思う。
https://twitter.com/kota222studying/status/1468218342679150593
#統計 特別なモデルに依存しない不偏推定量を作りたい人は「U統計量」について検索。
#統計 #Excel
えっ!びっくりしたのでググってみた。
ExcelのT.DIST関数の解説に、確かに
【分布の自由度を整数で指定します。】
と書いてありました!
統計がらみではJulua, R, Pythonしか使わないので知りませんでした。
普通はt分布の自由度は正の実数全体。
support.microsoft.com/ja-jp/office/t…
えっ!びっくりしたのでググってみた。
ExcelのT.DIST関数の解説に、確かに
【分布の自由度を整数で指定します。】
と書いてありました!
統計がらみではJulua, R, Pythonしか使わないので知りませんでした。
普通はt分布の自由度は正の実数全体。
support.microsoft.com/ja-jp/office/t…
https://twitter.com/tchaikovsky1026/status/1468256582836588545

某大きな大学の某学部の統計学も専門らしい先生が「データサイエンスの教育でRは使わない方がよくてExcelを使うべきだ」と言ったという話を聞いたことがある。
めちゃくちゃまずすぎると思いました。
めちゃくちゃまずすぎると思いました。
• • •
Missing some Tweet in this thread? You can try to
force a refresh