Thread by @keenanisalive

Suppose you have a pair of handcuffs linked together. Can you pull them apart without unlocking or breaking them, or letting them pass through themselves? With real handcuffs, definitely not! But if they're made of stretchy rubber, it turns out to be possible—as shown here. 1/9

This motion provides a surprising example of what is known in mathematics as an "ambient isotopy" of two surfaces: a continuous motion where the surface is not ripped, cut, pinched, or allowed to pass through itself. 2/9

A more classic example is the "unknot problem": given a loop of string, can it be untangled into a circle without cutting? Even this simple question turns out to be very hard to answer in general. And only gets harder when you start thinking about surfaces rather than curves. 3/9

So how do you find an isotopy that unlinks the handcuffs? Over the years, people have made all sorts of drawings of this transformation—but they can be pretty hard to follow unless you already have a pretty good geometric imagination! 4/9

The unlinking motion in the video above was computed in a particularly remarkable way: it was not keyframed or manipulated by a human animator, but computed automatically by a program that does not do any high-level reasoning (or machine learning!). 5/9

Instead, it minimizes an energy that knows only about the shape of the surface at the current moment in time. Just like gravity makes a ball fall to the ground, this so-called tangent-point energy makes a surface "fall" into the configuration that maximizes self-separation. 6/9

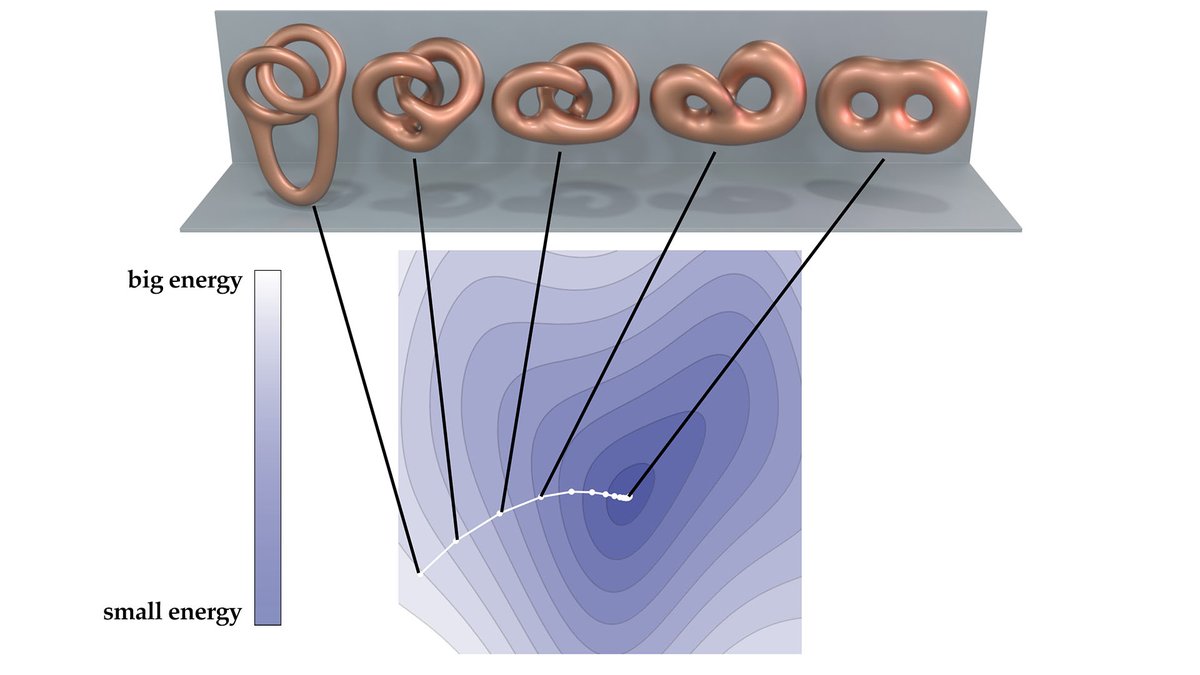
To make the movie, we minimize the energy from both the "linked" and "unlinked" starting points. Then we reverse the second movie, and join them together. 7/9

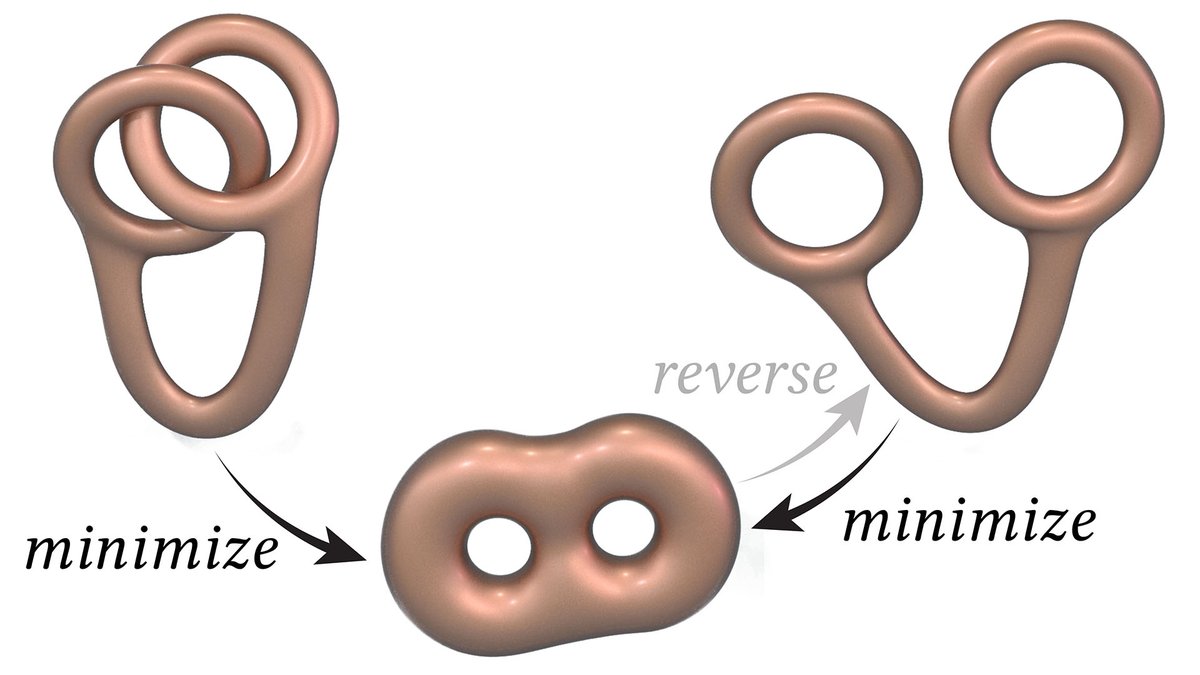
By the way, this idea of connecting two surfaces—or other objects—through a canonical object is a powerful idea in mathematics, and also the starting point for a lot of computational algorithms (such as shape correspondence):

https://mobile.twitter.com/keenanisalive/status/1420452422498099201

8/9

In this case, the algorithm used to minimize energy comes from the paper

Yu, Brakensiek, Schumacher, and Crane
"Repulsive Surfaces"
SIGGRAPH Asia (2021)

For more information, see cs.cmu.edu/~kmcrane/Proje…
and


9/9

You can also find a looping video of the handcuff unlinking here:



I'll be posting some more fun examples of "mathematical magic" throughout the week, so stay tuned!