#統計 いやあ、これにはマジでびっくりした。😱
ベイズ版95%信用区間(確信区間)がゼロをまたがなくなるまでNを増やす行為は、P値が5%を切るまでNを増やすp-hacking行為と(小さな誤差を除けば)数学的に同等です。
P値が5%を切るまでNを増やすp-hacking行為の是非も規範の問題で済ませられる?
ベイズ版95%信用区間(確信区間)がゼロをまたがなくなるまでNを増やす行為は、P値が5%を切るまでNを増やすp-hacking行為と(小さな誤差を除けば)数学的に同等です。
P値が5%を切るまでNを増やすp-hacking行為の是非も規範の問題で済ませられる?
https://twitter.com/genkuroki/status/1470260656368922626
#統計 2020年3月に出版された豊田秀樹さんの本には、ベイズ統計では【データを取り増しても】よいし【事前登録~も必要ありません】と言っています。(他にも色々!)
これを「ベイズ統計を使えば研究不正扱いされていたことを堂々とできるようになる」と解釈する人達が出ることを危惧していました。
これを「ベイズ統計を使えば研究不正扱いされていたことを堂々とできるようになる」と解釈する人達が出ることを危惧していました。
https://twitter.com/genkuroki/status/1339343675239776258

#統計 より正確に言えば、同様の言説を他で見た人達が、「ベイズ統計を使えば研究不正扱いされていたことを堂々とできるようになる」と既に信じている場合もあるのではないかと思いました。
これ、めちゃくちゃまずくないですか?
これ、めちゃくちゃまずくないですか?
#統計 数学的に「P値が5%未満になる」とほぼ同値になることが前もって分かっている条件を、「ベイズ統計では規範(主義)が違うからデータ取得の終了条件として採用してよい」とするのは非常にまずい。現実の科学研究でそれをやる人達が出て来たらどうする?
Bayes hacking
errorstatistics.com/2017/04/01/er-…
Bayes hacking
errorstatistics.com/2017/04/01/er-…
https://twitter.com/genkuroki/status/1342262365488738305

#統計 どういう話であるかを解説
ここに偶数と奇数の目が同じ確率で出るイカサマでないサイコロXがあったとします。
そして、「サイコロXの出目の偶奇に偏りがない」という仮説を否定したい人が
「その仮説が有意水準5%で棄却されるまでサイコロを振り続けてやる」
と言った。続く
ここに偶数と奇数の目が同じ確率で出るイカサマでないサイコロXがあったとします。
そして、「サイコロXの出目の偶奇に偏りがない」という仮説を否定したい人が
「その仮説が有意水準5%で棄却されるまでサイコロを振り続けてやる」
と言った。続く
#統計 数学的に理想化された設定では、その人はサイコロを繰り返し振って、出目のデータを順序増やして行くことによって、確率1でいつかは「サイコロXの出目の偶奇に偏りがない」という仮説の二項検定におけるP値を5%未満にできます。
続く
続く
#統計 実際に成功したその人は
「ほら、サイコロXの出目の偶奇は偏っているじゃないか!
もちろん、サイコロXの出目の偶奇が偏っていなくても、
5%の確率でその仮説は棄却されちゃうので、
完璧にサイコロXがイカサマなことを
証明できたわけではないんだけどね」
とデタラメを言った。続く
「ほら、サイコロXの出目の偶奇は偏っているじゃないか!
もちろん、サイコロXの出目の偶奇が偏っていなくても、
5%の確率でその仮説は棄却されちゃうので、
完璧にサイコロXがイカサマなことを
証明できたわけではないんだけどね」
とデタラメを言った。続く
#統計 その人は、実際にはサイコロの出目の偶奇が偏っていなくても確率1で成功する作業をやっただけなのに、5%の低い確率でしかそうならないかのような印象操作をしようとしているわけです。
その人の名前はP.ハッキング。
続く
その人の名前はP.ハッキング。
続く
#統計 そこにベイズ統計に詳しい別の人(仮にB氏と呼ぶ)がやって来て、「P.ハッキング氏は頻度主義統計学のルールを違反している」と言いました。
さらにこう言った。「ベイズ統計ならば尤度原理を満たすので、サイコロの出目のデータをどのように止めたかに推論の結果は依存しませんよ」と。続く
さらにこう言った。「ベイズ統計ならば尤度原理を満たすので、サイコロの出目のデータをどのように止めたかに推論の結果は依存しませんよ」と。続く
#統計 そのB氏は、ベイズ統計の95%信用区間から「偶数が出る確率=0.5」が除外されるまで、サイコロを振り続けた。
そしてこう言った。「P.ハッキング氏は頻度主義統計学のルール違反をしていたが、結論だけは正しかった。ベイズ統計でも95%信用区間から『偶数が出る確率=0.5』は除外された」と。
そしてこう言った。「P.ハッキング氏は頻度主義統計学のルール違反をしていたが、結論だけは正しかった。ベイズ統計でも95%信用区間から『偶数が出る確率=0.5』は除外された」と。
#統計 これを見ていた聴衆の一人がB氏にこう聞いた。
「ベイズ統計ではnullをまたがないようになるまでNを増やし続けても、95%信用区間の95%の意味は変わらないのですか?」
B氏は「事後分布の意味合いはどうNに達したかによらない」
続く
「ベイズ統計ではnullをまたがないようになるまでNを増やし続けても、95%信用区間の95%の意味は変わらないのですか?」
B氏は「事後分布の意味合いはどうNに達したかによらない」
続く
#統計 実際、ベイズ統計での事後分布は、尤度函数が定数倍しか違わないと、同じになります。
そして、これが「規範の問題」であることをB氏は強調した。
この実演を見ていた聴衆達はベイズ統計ならば自分が否定したい仮説が否定されるまでデータを取り続ければ良いことを「理解」して満足した。続く
そして、これが「規範の問題」であることをB氏は強調した。
この実演を見ていた聴衆達はベイズ統計ならば自分が否定したい仮説が否定されるまでデータを取り続ければ良いことを「理解」して満足した。続く
#統計 以上でこれがどういう話であるかの解説を終えます。
私は、実際に、聴衆達がベイズ統計ならば自分が否定したい仮説が否定されるまでデータを取り続ければ良いことを「理解」して満足してしまうことを心配しているわけです。
それは理解ではない。
私は、実際に、聴衆達がベイズ統計ならば自分が否定したい仮説が否定されるまでデータを取り続ければ良いことを「理解」して満足してしまうことを心配しているわけです。
それは理解ではない。
#統計 自分でコンピュータシミュレーションで遊びたい人は
nbviewer.org/github/genkuro…
を参照。 #Julia言語
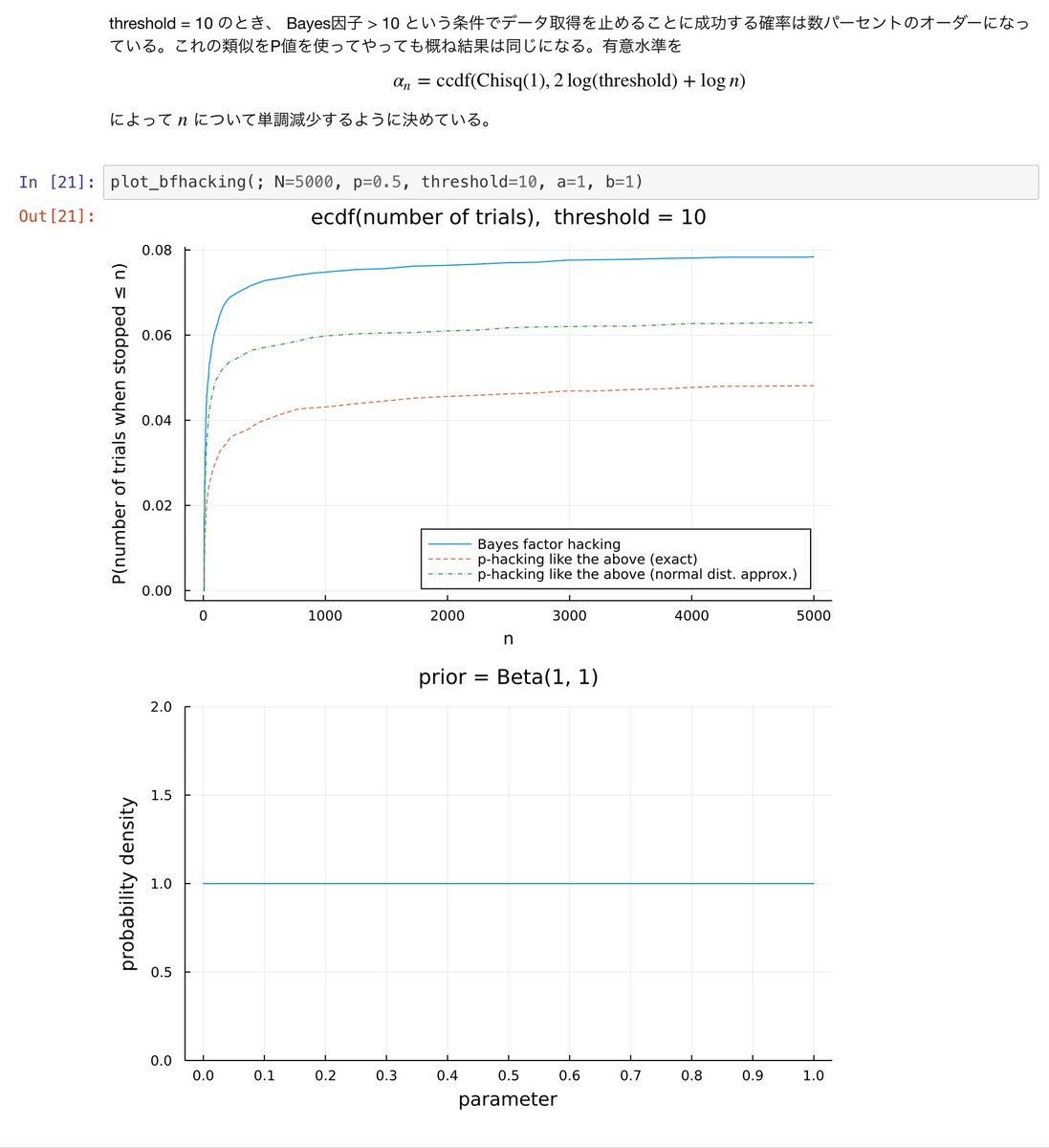
正規分布近似によるP値 < 5% とすることにP.ハッキング氏がn回までに成功する確率は緑の破線です。
ベイズ版95%信用区間から0.5を外すことにB氏がn回までに成功する確率は青線です。
nbviewer.org/github/genkuro…
を参照。 #Julia言語
正規分布近似によるP値 < 5% とすることにP.ハッキング氏がn回までに成功する確率は緑の破線です。
ベイズ版95%信用区間から0.5を外すことにB氏がn回までに成功する確率は青線です。
https://twitter.com/genkuroki/status/1470013177782243330

#統計 B氏はこう言うかもしれない。
「その青線で示された確率は,頻度主義統計学の標本分布で測った確率であり、ベイズ主義では標本分布は使用しない。このように、頻度主義とベイズ主義の規範は違うのだから、そのような比較は無意味である」と。
まあ本当に言ったら、あきれてしまうのですが。
「その青線で示された確率は,頻度主義統計学の標本分布で測った確率であり、ベイズ主義では標本分布は使用しない。このように、頻度主義とベイズ主義の規範は違うのだから、そのような比較は無意味である」と。
まあ本当に言ったら、あきれてしまうのですが。
注意・警告:P.ハッキング氏もB氏も実在の人物ではありません(特にB氏)。その二人は私が話を分かりやすくするために作った仮想的な人物です。類似の発言をしている人を発見しても勘違いしないよう、お願いいたします。😝
#統計 #Julia言語
件のノートブックを更新
nbviewer.org/github/genkuro…
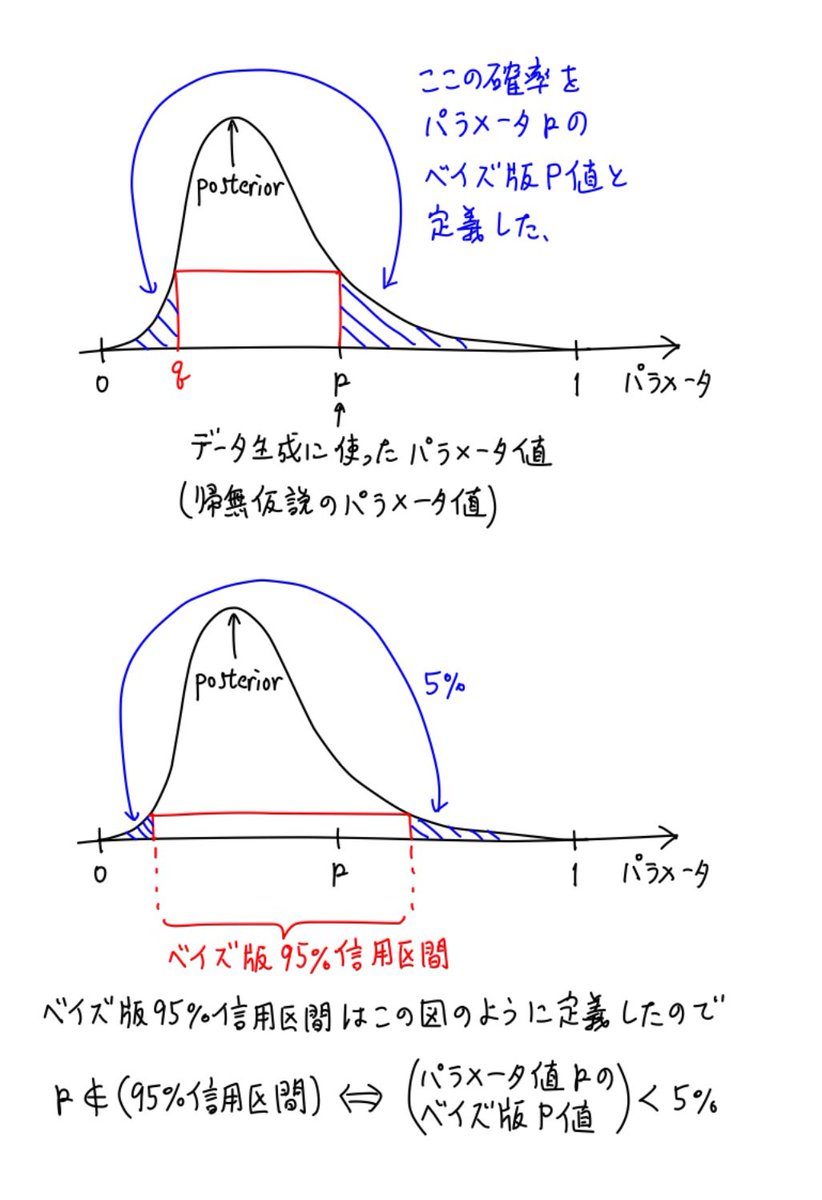
添付画像①②の青線は③のように定義されたベイズ版でのP値の類似物です。事後分布だけを使って定義されています。
緑のdashdot線が二項分布の正規分布近似によるP値で、ベイズ版のP値によく一致しています。


件のノートブックを更新
nbviewer.org/github/genkuro…
添付画像①②の青線は③のように定義されたベイズ版でのP値の類似物です。事後分布だけを使って定義されています。
緑のdashdot線が二項分布の正規分布近似によるP値で、ベイズ版のP値によく一致しています。



#統計 #Julia言語
nbviewer.org/github/genkuro…
添付画像を見ればわかるように、「n回中k回成功」のデータのn=100, k=30の場合では、ベイズ版のP値と正規分布近似による二項検定のP値はほとんどぴったり一致しています。
nbviewer.org/github/genkuro…
添付画像を見ればわかるように、「n回中k回成功」のデータのn=100, k=30の場合では、ベイズ版のP値と正規分布近似による二項検定のP値はほとんどぴったり一致しています。

#統計 ベイズ版のP値は
パラメータがベイズ版95%信用区間に含まれない
⇔ ベイズ版P値 < 5%
が成立するように定義してあるので、ベイズ版P値と通常の検定のP値の一致は、「パラメータがベイズ版95%信用区間に含まれないこと」と「通常のP値 < 5%」がほぼ同値であることを意味しています。
パラメータがベイズ版95%信用区間に含まれない
⇔ ベイズ版P値 < 5%
が成立するように定義してあるので、ベイズ版P値と通常の検定のP値の一致は、「パラメータがベイズ版95%信用区間に含まれないこと」と「通常のP値 < 5%」がほぼ同値であることを意味しています。
#統計 純粋に数学的な理由から(ゆえに誰も否定できない)、件のノートブックで扱ったケースでは「パラメータ値がベイズ版の95%信用区間から外れる」という条件と「通常のP値が5%未満になる」という条件は実践的には同じだと思ってよいです。nが十分大きいならほとんどぴったり一致している。
#統計 だから、「『偶数が出るの確率=0.5』という仮説のP値が5%未満になるまでデータを取得し続ける」と「偶数が出る確率のベイズ版95%信用区間に0.5が含まれなくまでデータを取得し続ける」は実践的にはほぼ同じことをやっているとみなせます。純粋に数学的に言えることなので誰も否定できない。
#統計 「『偶数確率=0.5』という仮説のP値が5%未満になるまでデータを取得し続ける」のはルール違反だが、「偶数確率のベイズ版95%信用区間に0.5が含まれなくまでデータを取得し続ける」のは構わないとしてしまうことは、同じ行為がルール違反になったりならなかったりするという主張とほぼ同じ。続く
#統計 もしかしたら、私が知らないベイズ統計の規範の中では、「偶数確率のベイズ版95%信用区間に0.5が含まれなくまでデータを取得し続ける」のが構わないことから、「『偶数確率=0.5』という仮説のP値が5%未満になるまでデータを取得し続ける」のも構わないということになっているかもしれません。😊
#統計 仮にそうなら、論理的な一貫性はあるのかもしれませんね。😝
#統計 訂正
❌「偶数確率のベイズ版95%信用区間に0.5が含まれなくまでデータを取得し続ける」
⭕️「偶数確率のベイズ版95%信用区間に0.5が含まれなくなるまでデータを取得し続ける」
「なる」が欠けていた。
❌「偶数確率のベイズ版95%信用区間に0.5が含まれなくまでデータを取得し続ける」
⭕️「偶数確率のベイズ版95%信用区間に0.5が含まれなくなるまでデータを取得し続ける」
「なる」が欠けていた。
• • •
Missing some Tweet in this thread? You can try to
force a refresh