Thread by @genkuroki

#統計 添付画像下段はよくあるベイズ版95%信用区間(確信区間)の最高事後密度(HPD)版です。95%の部分は0から1の間の任意の実数に一般化できる。

添付画像上段のベイズ版P値は「信頼区間と検定が表裏一体」という原理を適用して定義されています。

nbviewer.org/github/genkuro…

https://twitter.com/genkuroki/status/1470418590235262976

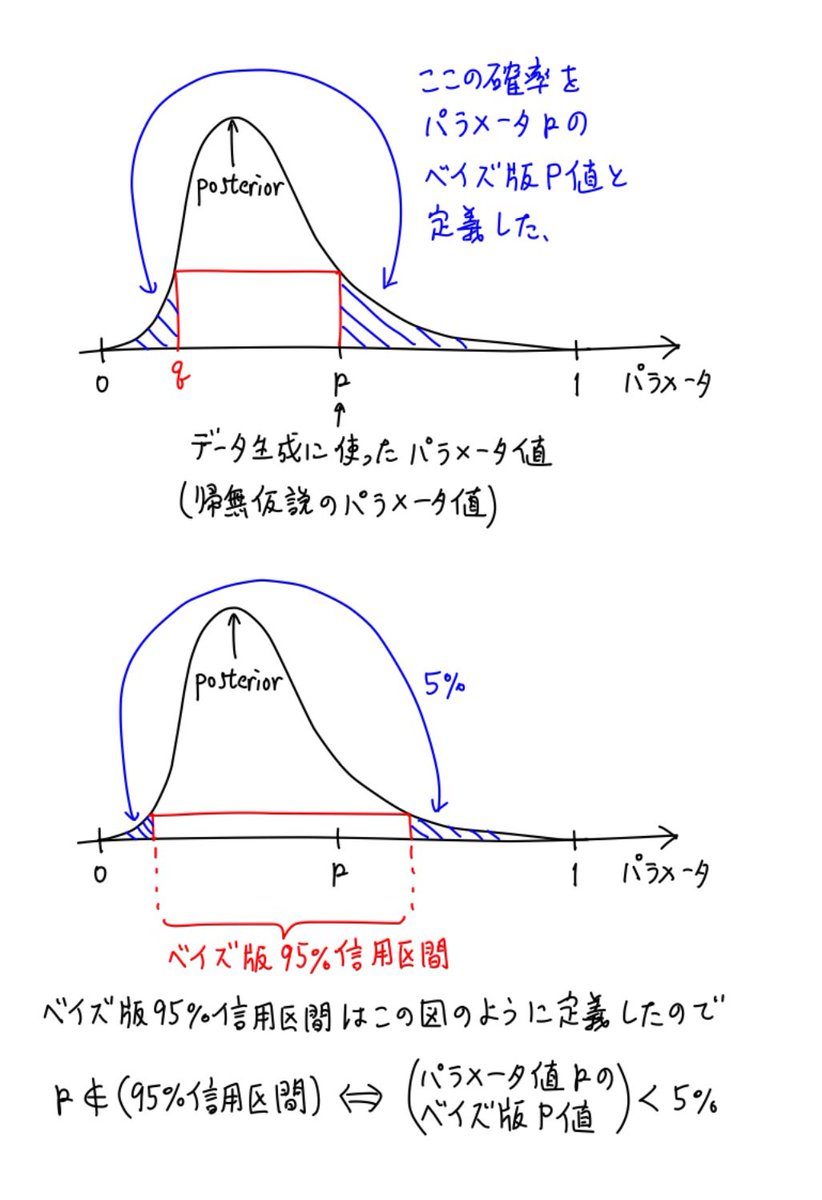
#統計 ベイズ版95%信用区間もベイズ版のP値も事後分布の情報だけを使って定義されており、通常の信頼区間やP値の作り方とは異なります。

しかし、数学には定義が全然違う量がある条件のもとでほぼ同じ値になることを証明できる場合が多数あって、解析学の基本的な考え方になっています。

#統計 実践的には無視できる違いしかない2つの数学的量を使った分析や推論は平等な扱いをする必要があります。

❌定義の違いは規範の違いから来ている。違いを無視できるほど同じ値になるとしても、それらは異なる使い方をされなければいけない。

などと言うと、単なるトンデモさんになってしまう。

#統計 信頼区間と検定の表裏一体性については以下のリンク先を見て下さい。

上で採用したベイズ版のP値の定義は、信頼区間と検定の表裏一体性における信頼区間をベイズ版信用区間に置き換えれば自然に出て来ます。

それは、事後分布の情報だけを使って定義されたP値の数学的類似物になる。

https://twitter.com/genkuroki/status/1469484030882385920

#統計 信頼区間や検定について知っている人は「ベイズ統計でのそれらの対応物は何か？」というもっともな疑問を持ちながら、「頻度論の信頼区間とベイズ統計の信用区間の意味の違い」(多くの場合デタラメ)を説明されて、疑問を表明することに躊躇したかもしれない。その答えがこのスレッドにある。

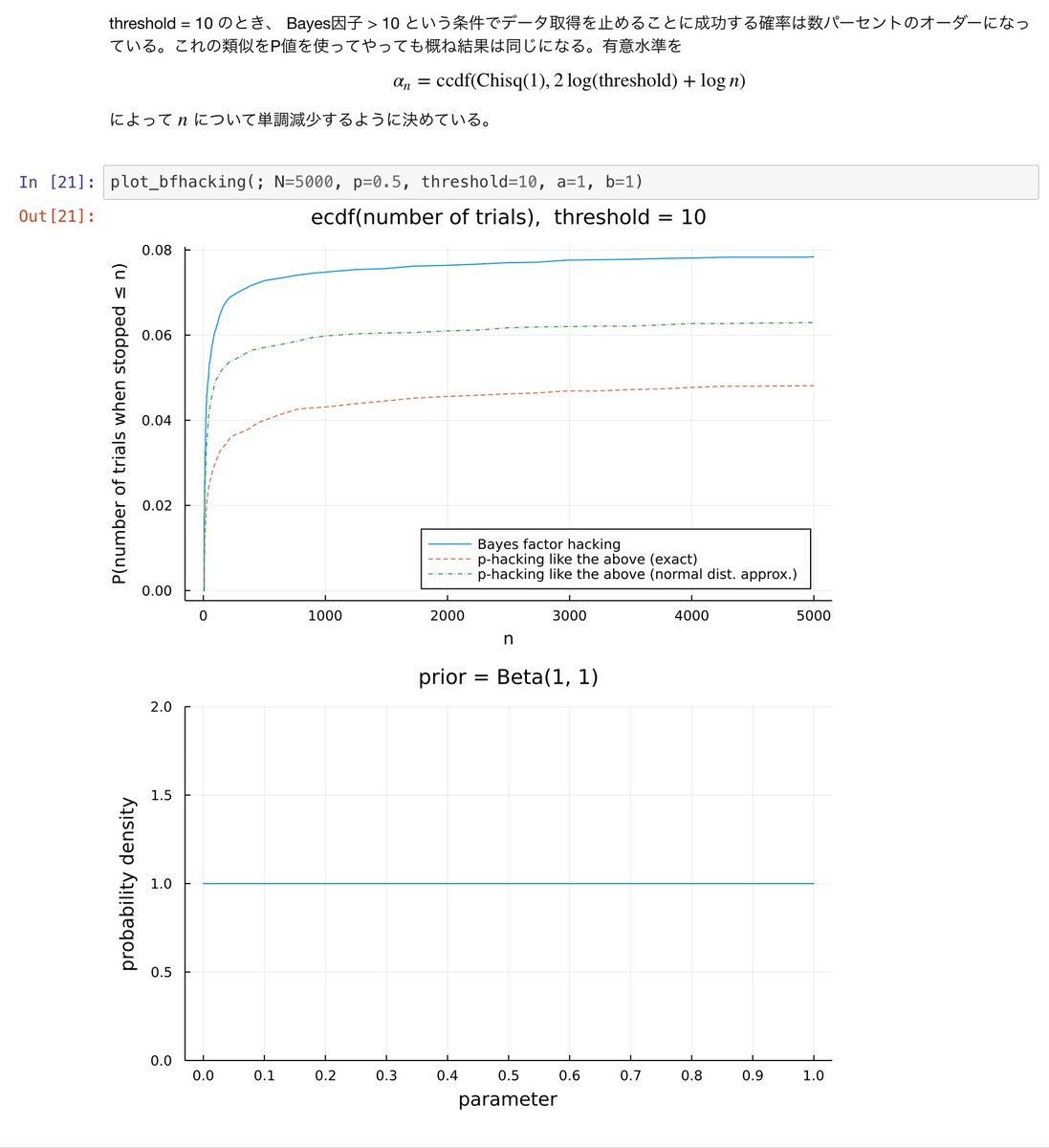
#統計 そして、ベルヌイ試行ような単純な統計モデルでは、nが十分大きなときには、通常の信頼区間やP値とベイズ版信用区間とベイズ版P値は数値的によく一致し、実践的にはそれらを区別する必要はなくなります。

コンピュータ上で使い慣れた道具の側を使えばよいと思います。

https://twitter.com/genkuroki/status/1470418586745606144

#統計 通常のP値については「P値 < α が実現するまでデータを順次取得」は所謂p-hackingで研究不正になります。

「ベイズ統計の95%信用区間から否定したいパラメータ値が除外されるまでデータを順序取得」はその研究不正行為と同じことをやっていることになることに注意が必要です。

#統計 その同じことになる理由は、数学的に定義がまったく異なる別に量の数値的な一致です。その一致は純粋に数学の話なので、「頻度主義 vs. ベイズ主義」というような規範や主義の違いに影響されません。

この点を無視して、めちゃくちゃなことを書き切った本が去年の3月に出た所謂豊田『瀕死本』。

https://twitter.com/genkuroki/status/1339343675239776258

#統計 #数楽 「定義がまったく異なる量の極限での一致」は数学では最も普通の面白い話題のパターンになっています。

そういう話題を楽しむ余裕があれば、おかしなことを言われても騙されずにすむ場合が増えます。

楽しめるようになれば相当に色々楽をできる。