Thread by @juliomulero

En muchos lenguajes de programación la instrucción a^b indica “a elevado a b”. La potencia de toda la vida, vaya. Así ocurre en R, por ejemplo.

Sin embargo, en Python, esto se escribe como a**b (dos asteriscos).

Hasta aquí, pues vale. ¡Pero sigue leyendo!⬇️⬇️

Hoy, en clase, una alumna me preguntó algo en lo que no había caído antes:

- Julio, pero entonces ¿qué resultado devuelve a^b en Python? Porque no da error. ¡Da un número!

Ahí he pensado “¿en serio?¿Y no da error? No sé, a saber…”.

Medio sorprendido, medio escéptico, le he respondido:

- Ahora no te lo sé decir, lo miro y os lo comento en las historias de Instagram (julio.mulero, por cierto).

Porque sí. No te sorprendas. Si quieres que se enteren de algo rápidamente, Instagram funciona a las mil maravillas.

Ni Twitter, ni ná (que me perdone Twitter 🙏). No sé los vuestros/as, pero los míos/as están en esa red social.

Total, que he llegado a casa y me he puesto comprobarlo con calma.

Y, efectivamente, por ejemplo, 3^5 devuelve 6 que obviamente no es “3 elevado a 5” (que sería 243). Pero tampoco habría sabido deducirlo.

¿Qué narices es?

Después de unas cuantas búsquedas, he llegado a lo que quería.

He de decir que no ha sido inmediato. De hecho, mi alumna también me lo advirtió. ¡Yo no lo he encontrado!

En primer lugar, debemos acudir a la representación binaria de los dos números (3 y 5) con los mismos cifras (poniendo ceros delante si es necesario). En particular, si tomamos tres cifras,

3 = 011 (en binario),
5 = 101 (en binario).

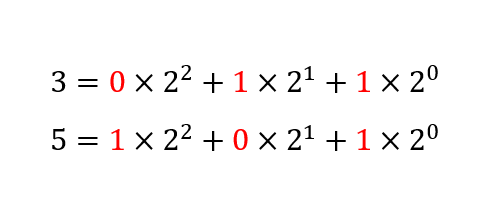
En segundo lugar, vamos comparando las cifras (0 ó 1) de cada número, posición a posición, y construiremos nuestro resultado.

Si las dos cifras son iguales, nuestro resultado tendrá un 0. En caso contrario, tendrá un 1.

Por ejemplo, las cifras más a la izquierda son:

Para el 3, un 0.
Para el 5, un 1.

Nuestro resultado tendrá un 1 en esa posición.

Para las cifras en la posición intermedia:

El 3 tiene un 1.
El 5 tiene un 0.

Nuestro resultado tendrá un 1 en esa posición.

Por último, las cifras más a la derecha son:

Para el 3, un 1.
Para el 5, un 1.

Nuestro resultado tendrá un 0 en esa posición.

Es decir, en binario, el resultado buscado se escribe como:

110.

Y aquí tenemos el 6.

6 = 110 (en binario).

Ok, pues muy bien. Al menos ya tenía la explicación por la que 3^5 vale 6 en Python.

Ahora bien, ¿qué es esto?

Bueno, sin entrar en muchos detalles, es un operador lógico bit a bit.

Un operador lógico actúa sobre dos operandos que pueden ser verdaderos o falsos y devuelve como resultado verdadero o falso. Habitualmente, 1 indica verdadero y 0, falso.

Existen muchos operadores lógicos. Por ejemplo:

x AND y: Devuelve verdadero si x e y son verdaderos.
x OR y: Devuelve verdadero si al menos uno de los dos es verdadero.
x XOR y: Devuelve verdadero solo si exactamente uno de los dos es verdadero.

De aquí salen las típicas tablas de verdad, considerando las dos opciones posibles para x e y:

1: Verdadero.
0: Falso.

El resultado de x^y está relacionado con el operador XOR. En concreto, se aplica este operador bit a bit.

Por eso, para las cifras más a la izquierda (o intermedias), que son un 0 y un 1, el resultado es 1.

Y para las cifras más a la derecha, que son 1 y 1, el resultado es 0.

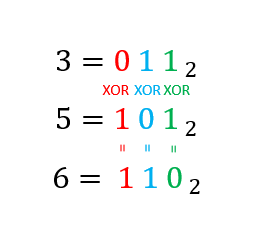
En resumen, en Python,

3^5 = 6.

Y esto se debe a un operador lógico (XOR) bit a bit.

Así que hoy, último lunes lectivo del año 2021, he aprendido algo nuevo gracias a mis alumnos/as.

Y ellos, desde este mediodía, lo tienen en Instagram y, desde este momento, en Twitter.

No dejemos de atender sus dudas porque, al fin y al cabo, ellos/as son el mejor combustible para que, como docentes, sigamos aprendiendo.

Y que conste que sigo sin ser ningún experto en esto. De hecho, si he metido alguna gamba, disculpadme.

Seguro que vosotros/as podéis enriquecer más este tema. ¡Y yo seguiré aprendiendo!