*Neural networks for data science* lecture 8 is out!
And it's already the last lecture! 🙀
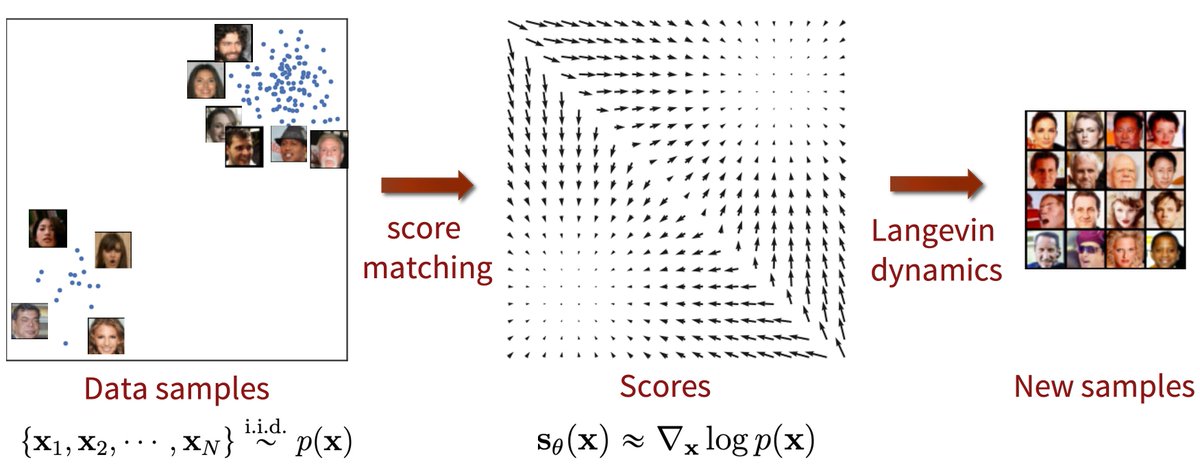
What lies beyond classical supervised learning? It turns out, _way_ too many subfields!
/n
And it's already the last lecture! 🙀
What lies beyond classical supervised learning? It turns out, _way_ too many subfields!
/n

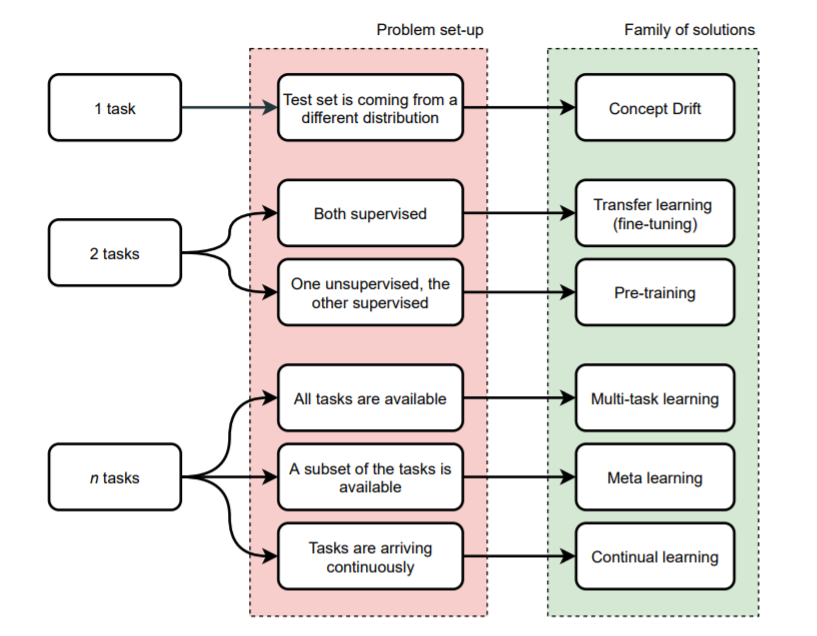
Here is my overview of everything that can happen when we have > 1 "task": fine-tuning, pre-training, meta learning, continual learning...
The slides have my personal selection of material. 😎
/n
The slides have my personal selection of material. 😎
/n
The slides are here: sscardapane.it/assets/files/n…
All the material, as always, is here: sscardapane.it/teaching/nnds-…
/n
All the material, as always, is here: sscardapane.it/teaching/nnds-…
/n
I have also a brand new lab session on multi-task audio classification, using #TensorFlow Hub, @huggingface Datasets, the pre-trained Wav2Vec porting by @7vasudevgupta, and a language identification dataset: 🤟
colab.research.google.com/drive/1KKusBkn…
colab.research.google.com/drive/1KKusBkn…

• • •
Missing some Tweet in this thread? You can try to
force a refresh