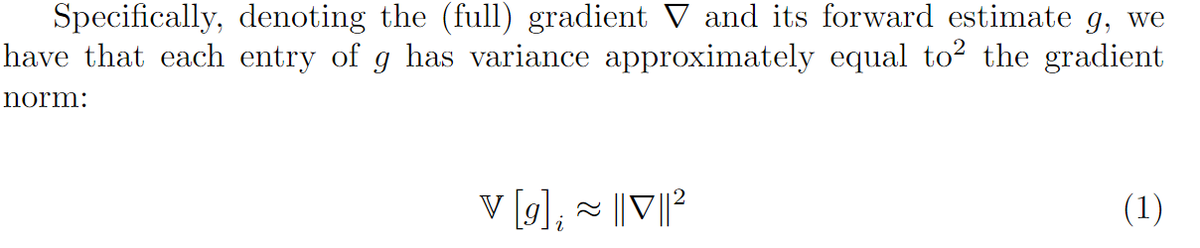Thread by @charles_irl

really cool new #AISTATS2022 paper presenting 1) a particular setting for model monitoring and 2) a provably optimal strategy for requesting ground truth labels in that setting.

plus a bonus example, and theorem, on why you shouldn't just do anomaly detection on logits!

https://twitter.com/james_y_zou/status/1498677901897654280

scene: data in real life is non-stationary, meaning P(X,Y) changes over time.

our model performance is based on that joint distribution, so model performance changes over time, mostly downwards.

this is bad.

it's the ML equivalent of dependency changes breaking downstream code

worse still, we don't even know when our performance is degrading, because we don't know what the right answer was.

the slogan: "ML models fail silently".

kinda like databases without monitoring, unlike things that fail loudly, like programs that halt or throw errors

we can often get the right answer, but it's expensive -- we need to ask humans or wait a long time for the label to appear naturally (e.g. in prediction).

so there's two costs to balance:
- the cost of being wrong and
- the cost of checking whether we are wrong

enter, stage left: this paper.

"It is desirable to balance two types of costs: the average number of queries ... and the monitoring risk"

for concreteness, the focus is on classification (labels and accuracy) rather than the general case (targets and arbitrary metric). but I bet the basic idea generalizes.

technical contribution: let's combine these two risks in a Lagrangian (like adding regularization to a loss) that tells us the amortized cost of a particular strategy for monitoring.

the general problem of distribution shift is impossible without assumptions.

they assume the existence of a "feature-based anomaly signal".

AFAICT, that means their model can only provide improvements over intermittent baselines if P(X) changes. but this isn't stated explicitly

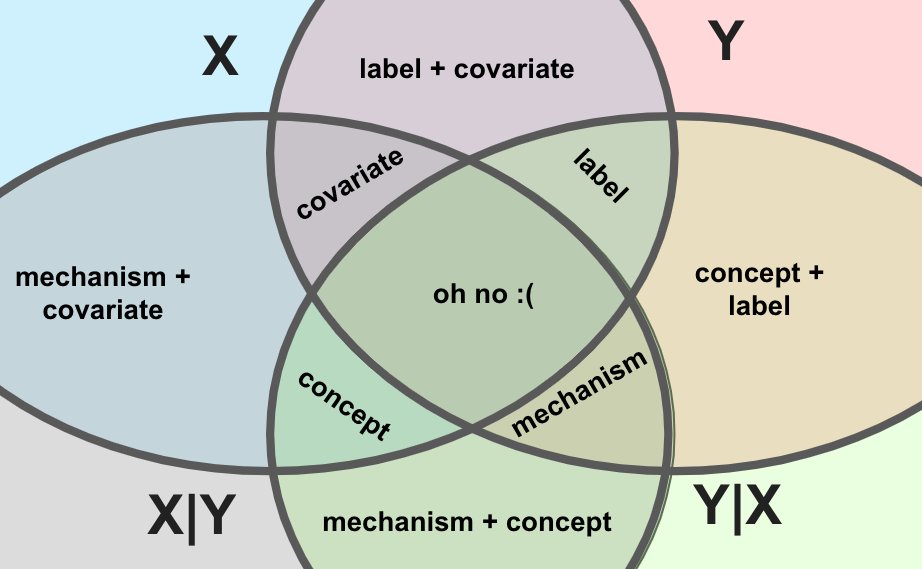
mapping this onto the popular typology of shifts: it can be an example of covariate shift or label shift, but _not_ concept drift.

it can also be neither, e.g. if P(X) and P(Y) and both conditionals are all changing together. that doesn't have a name, so i call it "a bummer".

(i wrote about the different types of drift in another thread, and you can learn much more about them from @chipro's linked blog post, from whence the screenshot above)

https://twitter.com/charles_irl/status/1497412218928779267?s=20&t=CdPffLpyWJNey1MsLjiQ_A

they make an additional assumption on the drift, coming more from the world of analysis.

they assume it doesn't happen "too fast", in a sense called _Lipschitz continuity_ of the _total variation_.

simpler terms: in one time step, the absolute difference can only be so much

fun fact from footnote 3: if the distribution is delta Lipschitz in total variation, then the accuracy is delta Lipschitz in absolute value.

If my intuition about that result holds, something similar should hold for other metrics in other problem settings, like squared error.

that brings me to what I see as two weaknesses of the paper.

all papers have weaknesses (and strengths), so this is emphatically not a knock on the work!

first, the Lipschitz assumption fails in some cases of practical interest.

if someone pushes a bug to prod anywhere in your ML system, your data can instantly become wet hot garbage.

garbage-in garbage-out means unbounded failure from there.

in some definitions of model monitoring, this is something you badly want to detect.

you can cover that case with other tools, e.g. @expectgreatdata, but ML system monitoring is a "belt-and-suspenders" or "defense-in-depth" kind of world.

second, absolute value is not really the best way to measure differences in accuracy.

consider: a sober driver is in an accident in roughly 1 in 10000 trips, an intoxicated driver in 2/1000.

that's 10x smaller than the absolute difference between a truly fair coin and a penny.

one is a matter of law and morality, the other is a piece of trivia.

sources for those numbers:

[1] ncbi.nlm.nih.gov/pmc/articles/P…

[2] statweb.stanford.edu/~cgates/PERSI/…

at the edges of performance (where we hope our models live!), ratios better map onto what we care about than absolute differences.

this difference is reflected in e.g. the fact that we use harmonic means with accuracies and other rates, rather than medians or means.

(terse mathy version: accuracy takes values between 0 and 1, differences between -1 and 1. we define absolute value on all reals, then inject [-1, 1] into them. it'd be better to use an isomorphism from [0, 1] to reals, e.g. a group iso, and to pull l2 or l1 along it)

that suggests there's still room for innovation even in the case (classification, continuous changes) they consider.

you'd need a different notion of Lipschitz continuity from a different metric/divergence on distributions.

Kolmogorov-Smirnov and Jensen-Shannon come to mind.

they also have a condition that is necessary for the model to be helpful over baseline: the "linear detection condition".

their method, MLDemon, uses a linear model to relate the anomaly detector to the accuracy signal. that only works if the signals are correlated.

this is not a blocking restriction in two ways:

1. the system can learn to ignore the linear model if it's not useful and revert to baseline over time.

2. you can replace the linear model with a nonlinear model and the algorithm still runs. you just lose any guarantees.

the theoretical analysis is dense (a novel extension of the Hoeffding inequality! in 2022!) and i'm still chewing through it.

but the top-line result is minimax optimality, up to logarithmic factors, matching baseline (periodic querying) in worst case.

Thm 4.1 (iii) above is a no-go theorem for RR, "request-and-reverify", which runs whenever the anomaly signal is above some threshold.

Notice in the above that its worst-case loss is Θ(1), which is trivial.

this comes from having a bad anomaly detector -- uncorrelated with the metric of interest.

you might counter that to rescue RR, we just need to add the ability to "discount" bad predictions.

but the linear case of that algorithm is just MLDemon!

this thread's getting pretty long, but we're almost done. let's see some empirical results to gut check the theory, then consider take-aways

the data streams are a really cool part of the paper. most benchmark datasets don't have a temporal component and data drift, so you need to add it artificially.

but they found some cool datasets, including a face dataset that captured the onset of widespread masking!

the core figure of results is figure 2, below.

upshot: MLDemon indeed never loses to periodic querying, unlike request-and-reverify, and sometimes it saves as much as 40% of query cost at the same model error level.

they actually prove that the improvement is at most about 2-4x in the happy case (Thm 4.3), which is pretty impressive as a degree of both knowledge of algorithm and agreement with empirical results.

more ML papers with this rigor please!

that's not a huge win -- not quite 2x, often only 1x -- so in my opinion the bigger result is the no-go.

restating their result in the negative: the strategy of trusting an anomaly detector is flawed, and in the ideal linear setting you can't do much better than periodic checks

that's a sobering result for people who care about model monitoring!

it makes me skeptical that a non-linear version (e.g. deep RL on choosing to query) can do much better. i wouldn't bet the farm on it and i'll be skeptical of the inevitable future results claiming otherwise

final closing note: one paper is always weak evidence, one twitter thread is still weaker.

and there's lots left to learn and discover about model monitoring and designing reliable ML systems

@james_y_zou @tginart @martinjzhang

i'm planning to talk on this paper at an MLOps journal club. i want to make sure i present your work accurately, so i'd be super grateful if you could give this thread a once-over and post (or DM) your thoughts

thanks for doing this work!