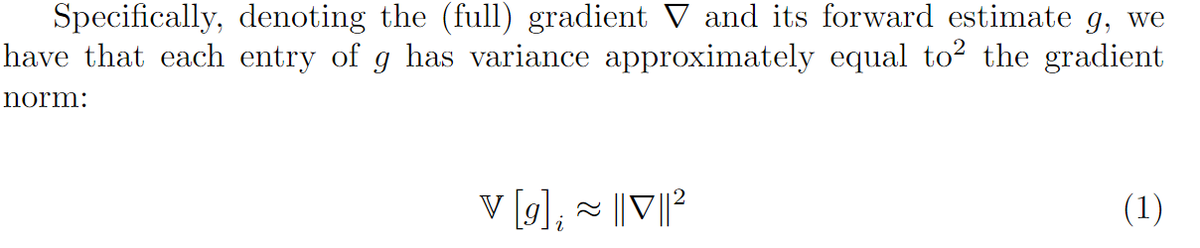last week i attended MLcon2.0 by @cnvrg_io and saw some great talks from all across the ML development stack
all of them are now available on-demand!
i'll call out some of my favorites here
cnvrg.io/mlcon-2
all of them are now available on-demand!
i'll call out some of my favorites here
cnvrg.io/mlcon-2
from @DivitaVohra, an overview of @Spotify's ML platform. super cool to hear how a product manager thinks about the problem of supporting ML systems


from @jeffboudier, an overview of the awesome work being done at @huggingface, with a focus on democratization of best practices, e.g. fast inference with Infinity


from @MarkMoyou of @nvidia, a really lucid overview of how to achieve low latency and high throughput in models on GPU. the visualization of sync/async GPU and CPU dataloaders is slick!








and last (in temporal order!) from my top 4, @LambdaAPI COO Mitesh Agrawal on how to build a datacenter for GPU-accelerated ML
🔑: different compute, storage, and networking needs for different parts of the pipeline (HPO, distributed training, inference)



🔑: different compute, storage, and networking needs for different parts of the pipeline (HPO, distributed training, inference)



• • •
Missing some Tweet in this thread? You can try to
force a refresh