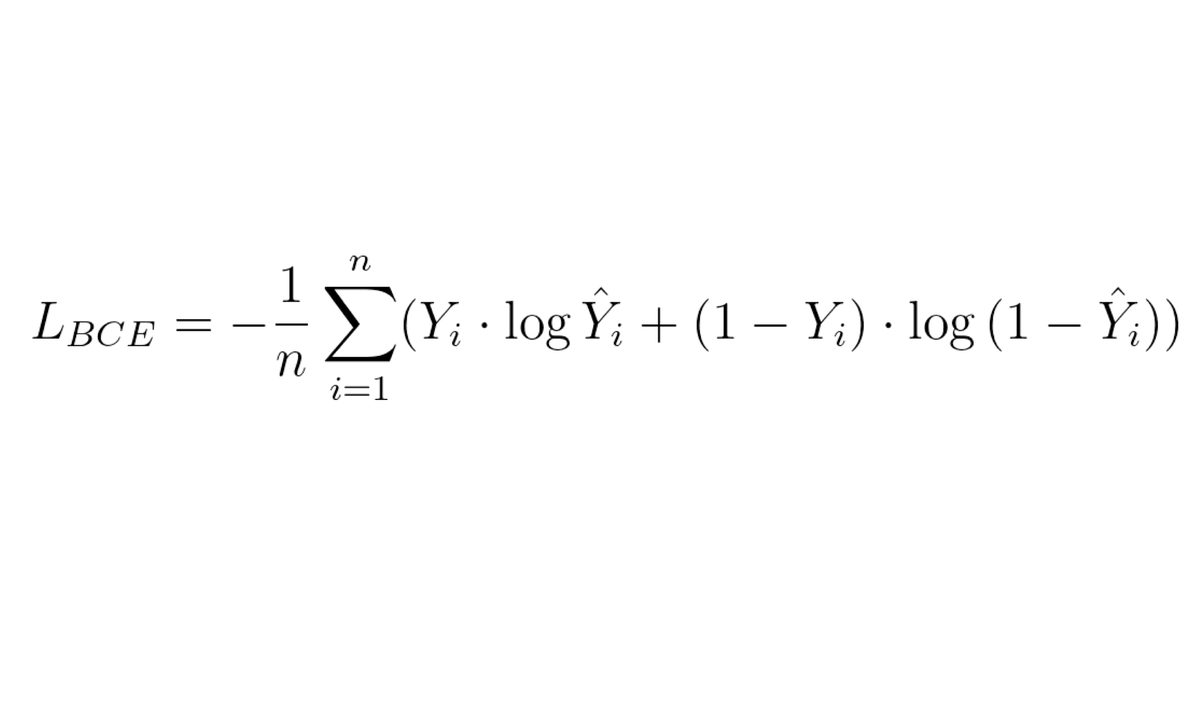Machine Learning Formulas Explained π¨βπ«
For regression problems you can use one of several loss functions:
βͺοΈ MSE
βͺοΈ MAE
βͺοΈ Huber loss
But which one is best? When should you prefer one instead of the other?
Thread π§΅
For regression problems you can use one of several loss functions:
βͺοΈ MSE
βͺοΈ MAE
βͺοΈ Huber loss
But which one is best? When should you prefer one instead of the other?
Thread π§΅
Let's first quickly recap what each of the loss functions does. After that, we can compare them and see the differences based on some examples.
π
π
Mean Square Error (MSE)
For every sample, MSE takes the difference between the ground truth and the model's prediction and computes its square. Then, the average over all samples is computed.
For details, check out this thread:
π
For every sample, MSE takes the difference between the ground truth and the model's prediction and computes its square. Then, the average over all samples is computed.
For details, check out this thread:
https://twitter.com/haltakov/status/1358852194565558276
π
Mean Absolute Error (MAE)
MAE is very similar to MSE, but instead of taking the square of the difference between the ground truth and the model's prediction, it takes the absolute value.
π
MAE is very similar to MSE, but instead of taking the square of the difference between the ground truth and the model's prediction, it takes the absolute value.
π
Huber Loss
The Huber loss is a combination of both ideas. It behaves like a square function (MSE) for small differences and like a linear function (MAE) for large differences.
I've written in detail about the Huber loss here:
π
The Huber loss is a combination of both ideas. It behaves like a square function (MSE) for small differences and like a linear function (MAE) for large differences.
I've written in detail about the Huber loss here:
https://twitter.com/haltakov/status/1501339290042880004
π
Alright, these loss functions are very similar in some aspects:
βͺοΈ They are always positive or 0
βͺοΈ The loss function increases if our model makes worse predictions
βͺοΈ They can be used for training machine learning models for regression
But there are important differences π
βͺοΈ They are always positive or 0
βͺοΈ The loss function increases if our model makes worse predictions
βͺοΈ They can be used for training machine learning models for regression
But there are important differences π
Handling outliers
Big differences between the ground truth and the prediction of the model are amplified by MSE much more than the others.
Imagine predicting a house price of 100K, while the real price is 50K. MSE will give us 2500K, while MAE and Huber loss only 50K.
π
Big differences between the ground truth and the prediction of the model are amplified by MSE much more than the others.
Imagine predicting a house price of 100K, while the real price is 50K. MSE will give us 2500K, while MAE and Huber loss only 50K.
π
Therefore, a model trained with MSE as a loss function will focus on removing the large outliers because they will dominate the loss function. Samples with a smaller error will practically be ignored.
This can be problematic if we don't care about big outliers.
π
This can be problematic if we don't care about big outliers.
π
Behavior around 0
MSE and the Huber loss are smooth around 0. This means that their derivative gets gradually smaller, which allows the optimization to converge nicely.
π
MSE and the Huber loss are smooth around 0. This means that their derivative gets gradually smaller, which allows the optimization to converge nicely.
π
MAE on the other hand has completely different gradients on both sides of the 0. This means that the optimization process may start oscillating when the error becomes small.
π
π
OK, but which one is best?
Well, there is no universal answer to this question (you saw that coming, don't you π). It really depends on your application and especially how you want to handle outliers.
Let's discuss two examples:
βͺοΈ House price predictor
βͺοΈ Trading bot
π
Well, there is no universal answer to this question (you saw that coming, don't you π). It really depends on your application and especially how you want to handle outliers.
Let's discuss two examples:
βͺοΈ House price predictor
βͺοΈ Trading bot
π
House prices
Imagine you are a real estate agent. You want an ML model that can estimate the price of a house given properties like its size, location, age etc. You want your model to predict the price so you can compare it with the listing price and find good deals.
π
Imagine you are a real estate agent. You want an ML model that can estimate the price of a house given properties like its size, location, age etc. You want your model to predict the price so you can compare it with the listing price and find good deals.
π
You will run your model over many listings and let it filter out potential good deals, which you will then review manually before taking a decision to buy.
A big outlier is not a problem there - if the model makes a very wrong prediction you will spot it and ignore it.
π
A big outlier is not a problem there - if the model makes a very wrong prediction you will spot it and ignore it.
π
In this case, it is probably a good idea to use MAE or the Huber loss, because you don't want to avoid huge errors in the model at any cost.
On the other hand, you want to model to be fairly accurate for most predictions, so you don't waste your time reviewing bad deals.
π
On the other hand, you want to model to be fairly accurate for most predictions, so you don't waste your time reviewing bad deals.
π
Automatic trading bot
Now imagine you are programming an ML model to predict stock prices and automatically buy and sell.
Things are different now - a big error of the model may lead to huge losses in a single trade! You don't want that.
π
Now imagine you are programming an ML model to predict stock prices and automatically buy and sell.
Things are different now - a big error of the model may lead to huge losses in a single trade! You don't want that.
π
In this case, you should rather use MSE, because it will penalize these huge errors. There may be more cases where the model makes smaller mistakes, but as long as it is profitable, this will not matter that much.
π
π
So, you see? Two different applications where we need different approaches. Sometimes MSE is better and sometimes MAE is better.
π
π
And the Huber loss?
It kind of combines the advantages of MAE for outliers and MSE for smoothness. However, it adds complexity with the additional hyperparameter Ξ΄. It essentially defines which errors are counted as outliers.
It is one more parameter you need to tune...
π
It kind of combines the advantages of MAE for outliers and MSE for smoothness. However, it adds complexity with the additional hyperparameter Ξ΄. It essentially defines which errors are counted as outliers.
It is one more parameter you need to tune...
π
Let me summarize
βͺοΈ MSE is good to avoid having large outliers
βͺοΈ MAE is better if you don't care about the outliers too much
βͺοΈ The Huber loss behaves like MAE for outliers but is smooth like MSE around 0
βͺοΈ The Huber loss comes with an additional hyperparameter to tune
π
βͺοΈ MSE is good to avoid having large outliers
βͺοΈ MAE is better if you don't care about the outliers too much
βͺοΈ The Huber loss behaves like MAE for outliers but is smooth like MSE around 0
βͺοΈ The Huber loss comes with an additional hyperparameter to tune
π
I regularly write threads to explain complex concepts in machine learning and web3 in a simple manner.
Follow me @haltakov for more
Follow me @haltakov for more
β’ β’ β’
Missing some Tweet in this thread? You can try to
force a refresh
γ
