Thread by @juliomulero

Un número primo es aquel que sólo es divisible por sí mismo y por la unidad (el 1 no se considera primo). Por ejemplo, el 2, el 3, el 5, el 7… ¿Fácil? No, porque son un misterio. La Hipótesis de Riemann habla sobre ellos y puede haber sido demostrada hoy mismo.

Dentro HILO 🔽

Los números primos son para el resto de números naturales como para nosotros nuestro código genético. En particular, todos los números son resultado de multiplicar números primos. Por ejemplo, 6=2x3, 15=3x5, 24=2^3x3… Esto es lo que se conoce como la factorización de un número.

Factorizar un número “pequeño” es fácil, pero qué pasa con un número que tiene, pongamos, 1000 cifras. Por ejemplo, ¿qué hacemos si queremos factorizar 2305843009213693951? El tema puede ser un auténtico rollo.

Primero, identificar todos los primos menores que su raíz (que son unos cuantos) y, segundo, dividir, dividir y seguir dividiendo. Después de un buen rato, tu conclusión será que este número es primo porque no puede ser dividido por ningún primo de forma exacta.

Pero, ¿cómo identificar los números primos? Hay algunos procedimientos sencillos como la criba de Erastótenes cuando implican pocos números. Se van eliminando los números que son múltiplos del 2, del 3, del 5… y, precisa y lógicamente, sólo sobrevivirán los primos.

Si te estás preguntando por qué es tan importante conocerlos, sólo tienes que pensar tu tarjeta de crédito y tus compras online. Tu clave debe debe ser segura ¿verdad? Algunos cifrados, como el método de clave pública RSA, se basan en la factorización de números enormes.

Por eso es clave, valga la redundancia, conocer cuáles son exactamente los números primos (y dónde se encuentran).

El misterio de los números primos ha fascinado a los matemáticos desde la antigüedad (aunque no existía Amazon ni eBay). Ya Euclides demostró que hay infinitos números primos, es decir, dado CUALQUIER número natural, siempre habrá primos más grandes que él.

Se sabe también que a medida que los números son más grandes, el número de primos va disminuyendo. Por ejemplo, entre 1 y 1000 hay 168 números primos, entre 100000 y 101000 hay 81, pero entre 10^100 y 10^100 +1000 sólo hay 2.

Los matemáticos se percataron de que el número de primos se iba estabilizando hacia un valor límite (pero no deja de crecer, ojo). Este estudio que, de primeras, se abordaba con técnicas puramente aritméticas, comienza a introducir funciones, límites, etc.

Si llamamos π(x) al número de primos menores o iguales que x, el objetivo es encontrar función conocida cuyo comportamiento sea “parecido”. Una llave para “desenmascarar” a π(x).

A partir de extensas tablas, Gauss (en 1798) intuye que para valores grandes de x la función π(x) es similar a la funcion x/ln(x) (ln(x) es el logaritmo neperiano de x). No os asustéis porque no entraremos en detalles.

La intuición de Gauss se confirma casi un siglo después, en 1896, cuando dos matemáticos el francés Jacques Hadamard, y el belga Charles de la Vallée-Poussin lo demuestran de forma independiente.

Unos años antes, en 1838, Dirichlet comunicó a Gauss que había encontrado otra aproximación a π(x), expresada como una función integral, que se denominó función logaritmo integral, Li(x), que se parecía aún más a π(x).

En 1737, Leonhard Euler, describe la siguiente función, conocida como zeta de Euler, a partir de una serie numérica (una suma con infinitos sumandos) y, a partir de ella, demostró la infinitud de los números primos.

Y después de 16 tuits llegamos a Riemann. Riemann se dio cuenta de que, si hacemos algunos cambios en la función de Euler, ésta no sólo podía hablarnos de la infinitud de los primos, sino de cómo se localizan.

Entre dichos cambios, Riemann apuesta por la generalización de la función zeta de Euler a los números complejos. Esos números son los s=a+bi donde a=Re(s) y b=Im(s) son números reales e i es la extraña raíz de -1 (la unidad imaginaria, imagínense).

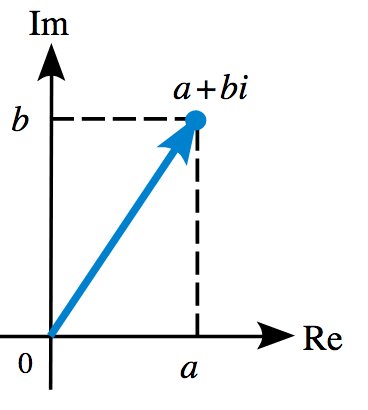
Esta variación de la función zeta de Euler, extendida a los números complejos, se conoció posteriormente como la función zeta de Riemann.

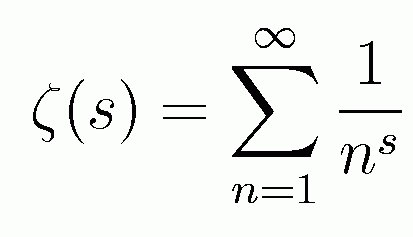
En un manuscrito, Riemann determinó que la distribución de los números primos estaba íntimamente relacionada con la distribución de los ceros no triviales de la función zeta (extendida ya a los números complejos).

En concreto, Riemann intuye que estos ceros se encuentran en la franja critica comprendida entre 0 < Re(s) < 1. Más concretamente, Re(s) = 1/2.

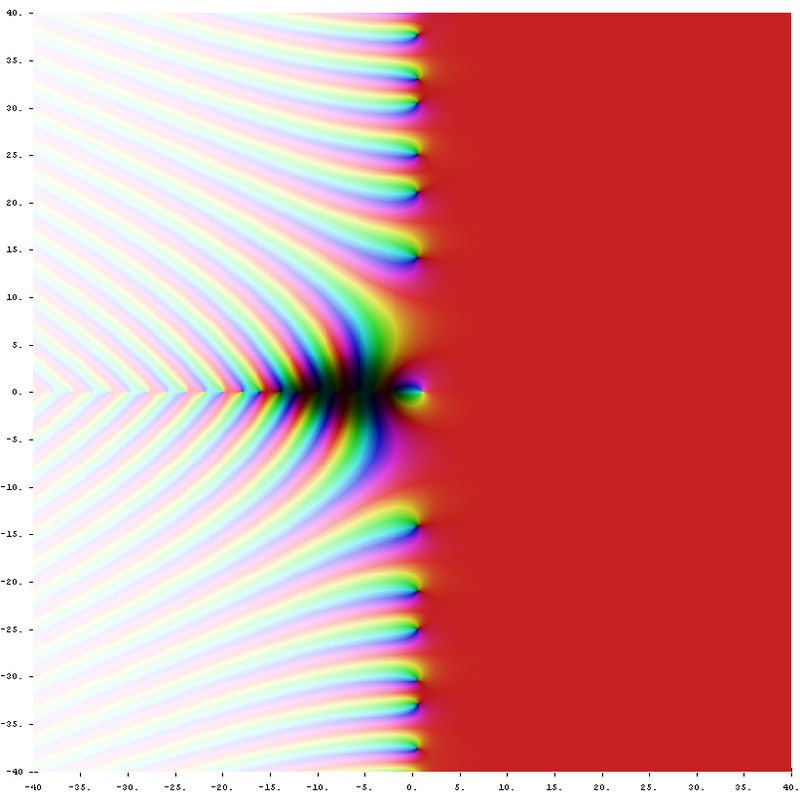
Desvelar el misterio de la hipótesis de Riemann es, por tanto, muy importante para la comunidad matemática. Muchos de los grandes matemáticos lo han intentado, sin éxito, pero haciendo mayores o menores aportaciones.

Y, no sólo es un empeño de los matemáticos, en parte el misterio en cuanto a la localización de los números primos es la salvaguarda de todo el comercio electrónico. Así que nos interesa, y mucho.

Ha habido muchas pruebas frustradas. De hecho, en los últimos años es frecuente que aparezcan nuevos intentos, que acaban fracasando. Como comprenderéis, la motivación va mucho más allá del millón de dólares que obtendría su autor por ser uno de los Problemas del Milenio.

Qué pasaría si la Hipótesis de Riemann fuera demostrada. Bueno, muchos otros resultados caerían como fichas de dominó. Algunos ya partieron en origen de la veracidad de la conjetura de Riemann.

Estimadores precisos del término del resto del teorema de los números primos, comparación de π(x) y Li(x) y, sobre todo, las distancias entre dos números primos consecutivos.

Por ejemplo, Cramer, en 1919, demostró que de ser cierta la Hipótesis de Riemann, existe una constante C tal que p_{k+1}−p_{k} = C √p_{k} log p_{k}, donde p_{k} es el k-ésimo primo. Tendríamos entonces localizados a nuestros queridos números primos.

Esta mañana Michael Atiyah (89 años), un matemático especialista en álgebra, lo ha intentado y quizás pase un poco de tiempo hasta verificar todo. Bienvenidos al espectáculo de las matemáticas.