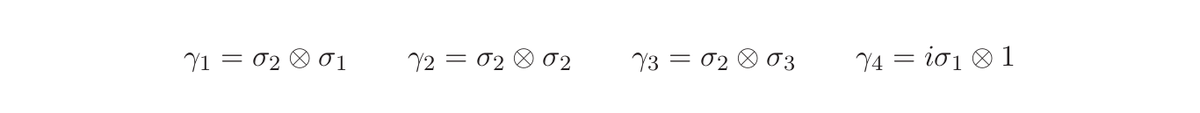careful, accepting sophisticated mathematical constructions only when they provide a clear simplification. And we should pare and unite existing structures whenever possible.
four dimensional base manifold. The electroweak and strong gauge fields
are described by Lie algebra valued connection 1-forms,
. u,. . . .}, with the spin connection and
principal bundle connection with everything,
Keywords: ToE.
selfdual) parts of the spin connection,
coordinates, is
for the spin connection, such as
frame, and fermions, in two coordinate systems.