Thread by @simon_tardivel

Allez, c'est reparti pour le cr3bp version Twitter. Au programme : comment orbiter autour... du VIDE !? 🤨

(Ou comment vulgariser la notion de "variétés centrales" d'un point d'équilibre)
👇👇👇

On commence par la fin: voilà ce qu'on peut faire autour d'un point de Lagrange.
😲😲😲
Mais comment est-ce possible ?!

Cher twitto, si tu débarques ici in medias res, je te conseille d'abord de lire le petit thread ci-dessous...

https://twitter.com/simon_tardivel/status/1230806252202135552

Repère synodique, points de Lagrange, barrière d'énergie, tout est bon ? Allons-y !

Les petites croix de mes animations précédentes, c'était donc bien les points de Lagrange. Ce sont des points d'équilibre : si on est EXACTEMENT dessus on ne bougera pas par rapport aux deux autres corps.

La preuve en vidéo (synodique à gauche, inertiel à droite, comme d'hab).

On comprend donc bien l'intérêt de ces points. Si on s'intéresse aux deux corps à la fois, c'est super pratique d'être entre les deux par exemple. On avait également vu avant que c'était des points qui permettaient de passer d'un corps à l'autre avec peu d'énergie. Ok ok ok...

Mais si on est PAS exactement dessus ? Que se passe-t-il ?
🤔
La question peut paraître n'intéresser que des matheux hardcore (c'est un peu vrai au fond 😆), mais la réponse révolutionne les trajectoires interplanétaires!

Parenthèse de nomenclature :
Les 3 points de Lagrange sur l'horizontale sont L1 (au milieu), L2 à droite, L3 à gauche.

Pourquoi les a-t-on mis dans cet ordre?

Je vous laisse revoir cette animation pour comprendre par vous-même... 😉

https://twitter.com/simon_tardivel/status/1230815940759228416

Les 2 autres points de Lagrange, qui forment un triangle équilatéral avec les 2 corps, s'appellent L4 (en haut) et L5 (en bas). Ils sont... compliqués, donc on n'en parlera pas.

Désolé.

Bref. Donc L1, L2, L3 sont des points d'équilibre *instables*. Si on est pas exactement dessus, alors on s'en éloigne. Très vite.

Exemple ici de l'effet d'une erreur de position de ~1km dans un système Terre-Lune (380'000km de distance hein... juste 1km d'erreur)

Deux remarques sur cette vidéo:
1. la Terre et la Lune ne sont PAS à l'échelle, mais si je les mets à l'échelle vous verrez rien du tout 😭 (enfin 2 pauvres pixels ci-et-là)
2. On a quitté le point L1 en moins d'une orbite de la Lune autour de la Terre, donc moins de 28 jours !

L'instabilité, ça se comprend intuitivement. Si on bouge un tout petit peu vers un côté, on est attiré plus de ce côté que l'autre. C'est comme essayer de faire tenir un crayon sur la pointe: ça ne marche que si la position est parfaite.

Mais, n'en restons pas là: que se passe-t-il exactement si on n'est pas au bon endroit?

Animation choc avec 100 exemples complètement aléatoires, en synodique, zoomé sur le point L1. J'insiste sur le caractère aléatoire: à quoi vous attendriez-vous? Probablement pas à ça...

Normalement ce fut un choc. Les trajectoires suivent toute une diagonale depuis L1 (et après ça tourne). Pas moyen d'en dévier ! On va pas dans tous les sens. Pas du tout !
😯😯😯
On appelle ce chemin particulier une *variété*. Et ici c'est la variété *instable* de L1.

Mais y'a plus cool encore... 🤓

Là, on regardait ce qui se passait dans le futur. Et si on regardait plutôt ce qui se passait dans le passé, en remontant le temps. Que doit on s'attendre à voir ?

(réponse au prochain tweet, pas de triche!!!)

La réponse.

(faudrait que je travaille un peu le click-bait non? 🤔 genre "Il propage son système dans le passé, vous ne devinerez jamais ce qu'il découvre ! CLICK CLICK PROMO"

Comment pouvait-on s'y attendre ? Parce que, inverser le temps, ça veut dire que les corps tournent dans l'autre sens. Donc qu'on renverse l'axe vertical du repère synodique. Donc on symétrise la diagonale.

BAM nous venons donc aussi de découvrir la symétrie "y-t" du cr3bp ! \o/

Mais il y a une autre catégorie de mouvement possible.

Si on fixe bien les conditions initiales, on n'est sur aucune de ces deux diagonales. Et donc reste éternellement autour du point de Lagrange. Mais il faut que les conditions initiales soient très bien choisies !

On ne va pas revenir vers le point de Lagrange, on ne va pas s'en éloigner, on va tourner autour. C'est ce qu'on appelle une variété *centrale*. Parce que le point de Lagrange est le centre de cette variété.

Et on orbite donc... le vide. 😯

Ces orbites sont des ellipses quand elles sont petites, et ça devient des haricots quand on leur taille augmente. La période augmente (de façon non linéaire = compliqué) avec leur taille.
Le graphe de droite vous permet d'ailleurs de mesurer la période de chaque orbite ! 🤔

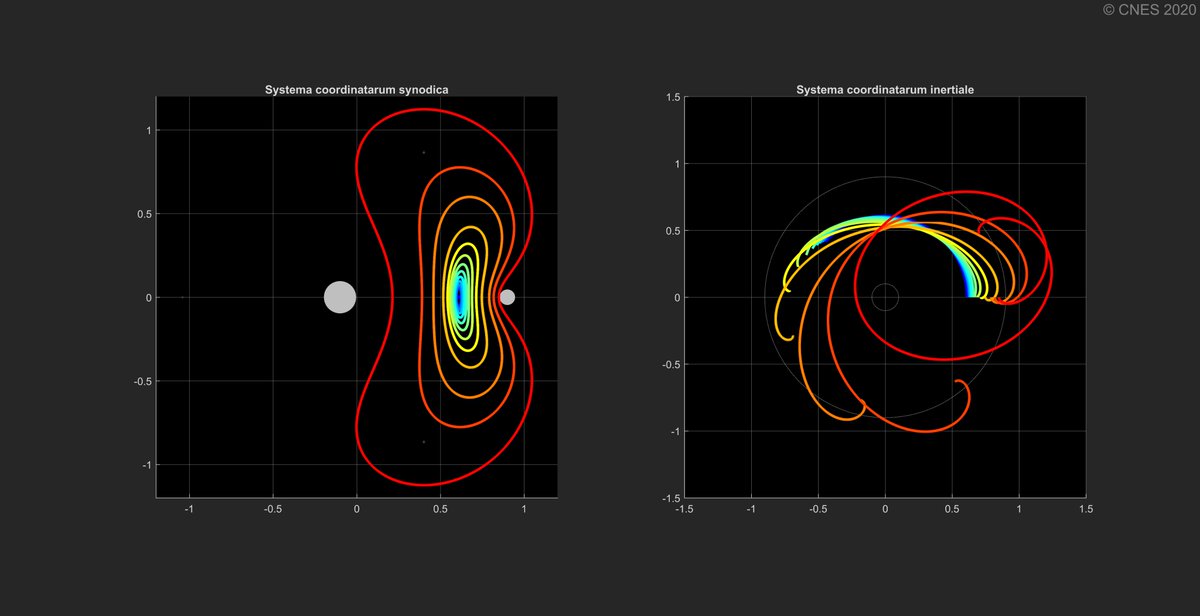
Si on synchronise la période avec celle des deux corps, alors on obtient de merveilleux motifs. On parle de résonnance N:P, quand l'orbite fait N tours alors que les 2 corps en font P.

Pour commencer, quelle résonnance voyait-on au début de ce fil ? 🤓

https://twitter.com/simon_tardivel/status/1233413824172167168

On voyait du 2:1. 2 tours du point Lagrange pour 1 tour des deux corps en inertiel.

Que commence alors la valse des rosaces ! Je ne vous en mets que 2 à chaque fois car sinon c'est illisible, on dirait qqun qui découvre le concept du spirographe.

Ici, du 3:2 et du 3:4.

Perso ce que j'adore sur cet exemple, c'est que dans le repère de gauche (synodique), les deux trajectoires tournent dans le même sens... mais dans le repère de droite (inertiel), elles tournent dans des sens inverses !!!

Et voilà maintenant un pentagramme ! Il met un moment à apparaître...

C'est du 5:2 et du 5:4.

On a donc vu aujourd'hui ce qu'il se passait près d'un point de Lagrange : comment s'en éloigner, comment s'en approcher et comment orbiter.

Mais, j'ai pas parlé d'orbite de Halo ! Hé oui, pour ça, il aurait fallu regarder ça en 3d...

Donc bah ce sera pour la prochaine fois😅