1/
Get a cup of coffee.
In this thread, I'll help you understand the basics of probability distributions and random variables.
Get a cup of coffee.
In this thread, I'll help you understand the basics of probability distributions and random variables.

2/
Imagine that you run an insurance company.
Every year, you write a policy that insures the city of San Francisco against an earthquake.
Imagine that you run an insurance company.
Every year, you write a policy that insures the city of San Francisco against an earthquake.

3/
Every year, on Jan 1'st, the city pays you an "insurance premium". You can invest this premium however you like.
If an earthquake hits, you need to pay the city $1B on Dec 31'st.
If no earthquake hits, you get to keep the premium -- and any returns you made by investing it.
Every year, on Jan 1'st, the city pays you an "insurance premium". You can invest this premium however you like.
If an earthquake hits, you need to pay the city $1B on Dec 31'st.
If no earthquake hits, you get to keep the premium -- and any returns you made by investing it.
4/
To take on this kind of "catastrophe risk", an insurance company must be well capitalized.
Let's say your insurance company starts with $2B of "equity capital". This is money belonging to the company's owners.
To take on this kind of "catastrophe risk", an insurance company must be well capitalized.
Let's say your insurance company starts with $2B of "equity capital". This is money belonging to the company's owners.
5/
The $2B equity capital is enough to pay for 2 years worth of earthquake damages.
But if there are 3 consecutive "earthquake years", the equity capital will be wiped out and the company will go broke -- unless of course investment returns are big enough to cover this damage.
The $2B equity capital is enough to pay for 2 years worth of earthquake damages.
But if there are 3 consecutive "earthquake years", the equity capital will be wiped out and the company will go broke -- unless of course investment returns are big enough to cover this damage.
6/
Let's say there's a 10% chance of an earthquake hitting San Francisco in any one year.
Also, let's say the city pays you $100M as premium at the start of each year.
And let's say you can get a 7% annual return on your investments.
Let's say there's a 10% chance of an earthquake hitting San Francisco in any one year.
Also, let's say the city pays you $100M as premium at the start of each year.
And let's say you can get a 7% annual return on your investments.
7/
The question is: what return can the insurance company's owners expect to earn -- on the equity capital they put up -- over the next few years?
The important thing to note is: this return is *not* deterministic.
The question is: what return can the insurance company's owners expect to earn -- on the equity capital they put up -- over the next few years?
The important thing to note is: this return is *not* deterministic.
8/
It's *probabilistic*.
It depends on chance events -- earthquakes hitting San Francisco.
There's a chance the company will get to keep all the premiums -- plus the investment returns earned on them.
There's a chance the company will go broke.
It's *probabilistic*.
It depends on chance events -- earthquakes hitting San Francisco.
There's a chance the company will get to keep all the premiums -- plus the investment returns earned on them.
There's a chance the company will go broke.
9/
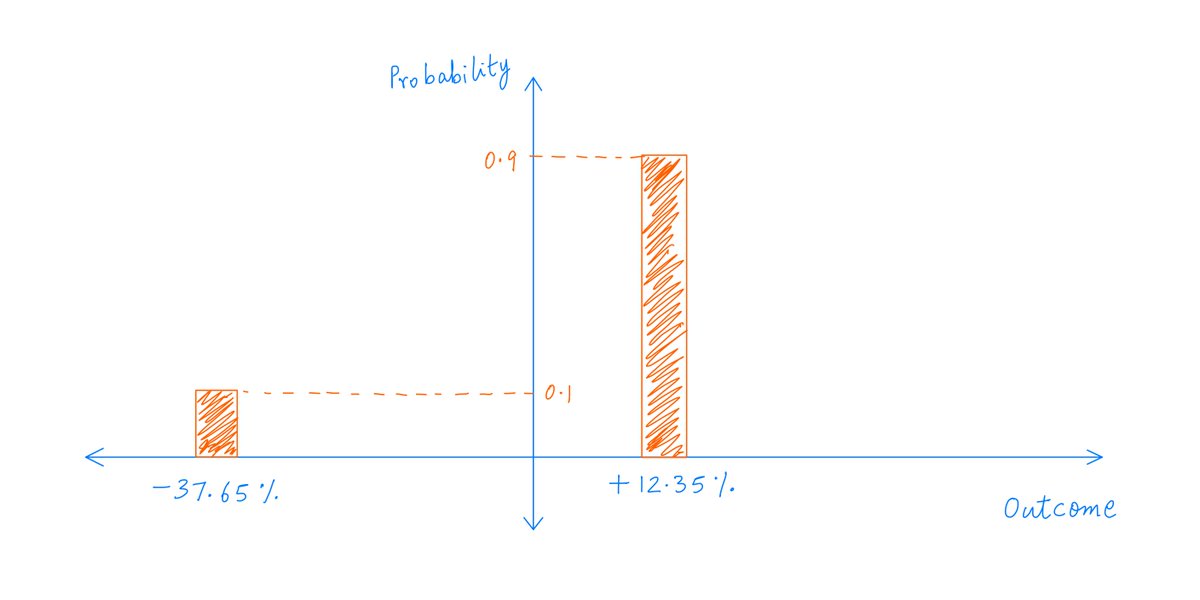
For example, at the end of 1 year, the company could end up with $2.247B -- the $2B of equity capital, plus the $100M premium, plus the 7% return on this $2.1B -- provided there's no earthquake.
This is a 12.35% return for the owners on their $2B capital.
For example, at the end of 1 year, the company could end up with $2.247B -- the $2B of equity capital, plus the $100M premium, plus the 7% return on this $2.1B -- provided there's no earthquake.
This is a 12.35% return for the owners on their $2B capital.
10/
But *if* there's an earthquake, the company will end up with only $1.247B -- the $2.247B it would have had if there were no earthquake, minus the $1B paid out in earthquake damages.
This is a *negative* 37.65% return for the owners.
But *if* there's an earthquake, the company will end up with only $1.247B -- the $2.247B it would have had if there were no earthquake, minus the $1B paid out in earthquake damages.
This is a *negative* 37.65% return for the owners.
11/
Also, these "return outcomes" aren't equally likely.
That's because the chance of an earthquake is only 10% -- not 50/50.
So, the +12.35% return has a probability of 0.9 (90% likelihood).
And the -37.65% return has a probability of only 0.1 (only 10% likelihood).
Also, these "return outcomes" aren't equally likely.
That's because the chance of an earthquake is only 10% -- not 50/50.
So, the +12.35% return has a probability of 0.9 (90% likelihood).
And the -37.65% return has a probability of only 0.1 (only 10% likelihood).
12/
We say that the return earned by owners on their equity capital is a "random variable".
In simple terms, a random variable is anything that has a range of outcomes depending on chance events.
In this case, our random variable has 2 possible outcomes: +12.35% or -37.65%.
We say that the return earned by owners on their equity capital is a "random variable".
In simple terms, a random variable is anything that has a range of outcomes depending on chance events.
In this case, our random variable has 2 possible outcomes: +12.35% or -37.65%.
13/
And as we saw above, the outcomes don't have to be equally likely -- they can have different probabilities.
So, what we have here is a list of possible outcomes, and a probability for each.
This is called a "probability distribution".
Every random variable has one.
And as we saw above, the outcomes don't have to be equally likely -- they can have different probabilities.
So, what we have here is a list of possible outcomes, and a probability for each.
This is called a "probability distribution".
Every random variable has one.
14/
We can draw pictures representing random variables and their probability distributions.
We just take the possible outcomes on the X-axis, and graph their respective probabilities on the Y-axis.
Like so:
We can draw pictures representing random variables and their probability distributions.
We just take the possible outcomes on the X-axis, and graph their respective probabilities on the Y-axis.
Like so:
15/
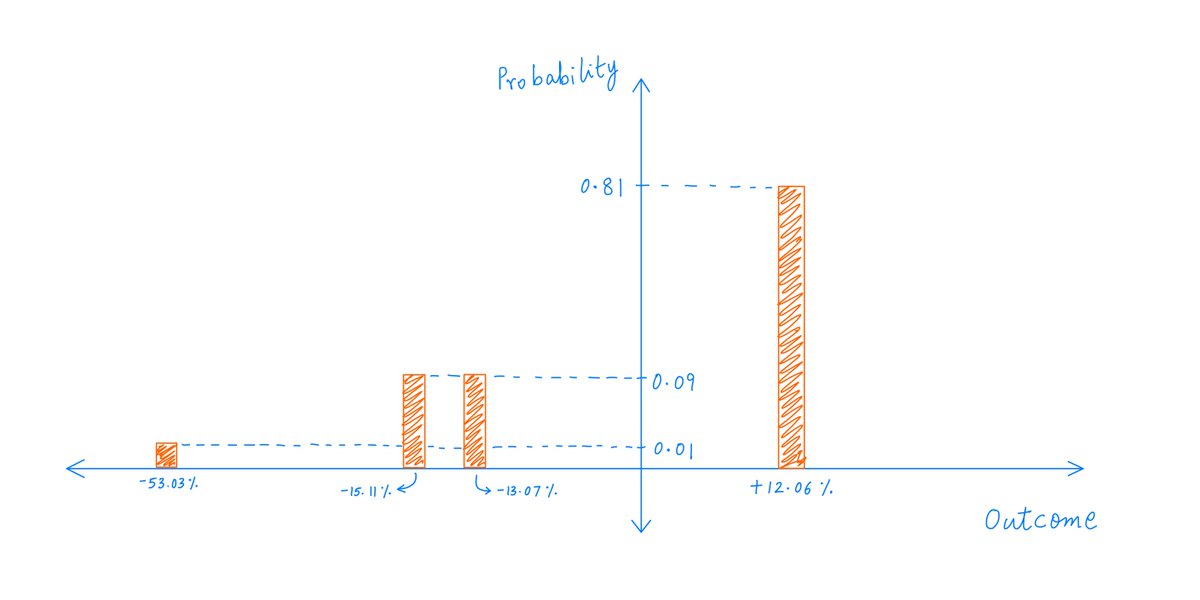
What if our insurance company looked 2 years out instead of 1 year?
Now, there are 4 possibilities -- each leading to a different "return outcome" for the owners:
What if our insurance company looked 2 years out instead of 1 year?
Now, there are 4 possibilities -- each leading to a different "return outcome" for the owners:

17/
In finance and investing, we often encounter random variables and probability distributions.
The returns we get depend on not just our own actions, but also chance events.
In practice, this makes it really hard to distinguish a good investment process from a bad one.
In finance and investing, we often encounter random variables and probability distributions.
The returns we get depend on not just our own actions, but also chance events.
In practice, this makes it really hard to distinguish a good investment process from a bad one.
18/
A good process (charging a reasonable premium, and investing it reasonably) can encounter a string of unlucky events (back to back earthquakes) and cause heavy losses.
A good process (charging a reasonable premium, and investing it reasonably) can encounter a string of unlucky events (back to back earthquakes) and cause heavy losses.
19/
By the same token, a bad process (charging highly inadequate premiums) can hit a lucky break (a string of earthquake free years) and create windfall profits.
By the same token, a bad process (charging highly inadequate premiums) can hit a lucky break (a string of earthquake free years) and create windfall profits.
20/
The best an investor can do is adopt a good process, and then hope for good luck.
So, what does a good process look like?
The best an investor can do is adopt a good process, and then hope for good luck.
So, what does a good process look like?
21/
First, a good process means understanding the various outcomes that can possibly happen -- and their probabilities.
Every investment is a random variable. The better we can judge its probability distribution, the better our process.
First, a good process means understanding the various outcomes that can possibly happen -- and their probabilities.
Every investment is a random variable. The better we can judge its probability distribution, the better our process.
22/
Sometimes, it can be hard to estimate the odds of a potential investment idea working out.
In this case, it may be best to just put this idea in the "too hard pile" -- as Buffett and Munger like to call it -- and move on to ideas that are easier to evaluate.
Sometimes, it can be hard to estimate the odds of a potential investment idea working out.
In this case, it may be best to just put this idea in the "too hard pile" -- as Buffett and Munger like to call it -- and move on to ideas that are easier to evaluate.
23/
For example, what are the odds of Microsoft Teams stealing significant market share from Slack over the next 10 years?
To be honest, I don't have the faintest idea.
Others may know the odds, and that's fine.
But I put Slack in my too hard pile.
For example, what are the odds of Microsoft Teams stealing significant market share from Slack over the next 10 years?
To be honest, I don't have the faintest idea.
Others may know the odds, and that's fine.
But I put Slack in my too hard pile.
24/
OK. Suppose we analyze an idea, and believe we have a reasonable estimate of the probability distribution of its returns.
What next?
Well, given this probability distribution, a good process asks the following questions.
OK. Suppose we analyze an idea, and believe we have a reasonable estimate of the probability distribution of its returns.
What next?
Well, given this probability distribution, a good process asks the following questions.
25/
Question 1. What is the best case scenario and its likelihood?
That is, is there sufficient upside?
Question 1. What is the best case scenario and its likelihood?
That is, is there sufficient upside?
26/
Question 2. What is the worst case scenario and its likelihood?
That is, is the downside tolerable?
Question 2. What is the worst case scenario and its likelihood?
That is, is the downside tolerable?
27/
Questions 3 and beyond. What is the average scenario? And what is the standard deviation around it?
What is the median scenario? And the most likely scenario?
Does this distribution have "long tails"? Do these tails provide surprises to the upside or downside?
Questions 3 and beyond. What is the average scenario? And what is the standard deviation around it?
What is the median scenario? And the most likely scenario?
Does this distribution have "long tails"? Do these tails provide surprises to the upside or downside?
28/
Looking at a probability distribution and deciding whether to bet money on it (and if so, how much money) -- is both art and science.
Some truly brilliant people have worked on this question -- and come up with all kinds of ingenious solutions.
Looking at a probability distribution and deciding whether to bet money on it (and if so, how much money) -- is both art and science.
Some truly brilliant people have worked on this question -- and come up with all kinds of ingenious solutions.
29/
These are for future threads.
But *this* thread is the first step -- recognizing the interplay between skill and luck, and accepting the fact that returns from most investment decisions are random variables, with a range of outcomes and probabilities.
These are for future threads.
But *this* thread is the first step -- recognizing the interplay between skill and luck, and accepting the fact that returns from most investment decisions are random variables, with a range of outcomes and probabilities.
30/
As usual, I'll leave you with a few references.
Buffett's letters are a great resource if you want to understand probabilistic thinking in insurance applications (like the earthquake insurance example above).
For example, here are excerpts from his 1997 and 2005 letters:

As usual, I'll leave you with a few references.
Buffett's letters are a great resource if you want to understand probabilistic thinking in insurance applications (like the earthquake insurance example above).
For example, here are excerpts from his 1997 and 2005 letters:


31/
The second chapter of @morganhousel's book is all about luck and risk.
The whole book is a great read. This chapter in particular underscores the role of chance events: a good process can make a good outcome more likely, but cannot guarantee it.
amazon.com/Psychology-Mon…
The second chapter of @morganhousel's book is all about luck and risk.
The whole book is a great read. This chapter in particular underscores the role of chance events: a good process can make a good outcome more likely, but cannot guarantee it.
amazon.com/Psychology-Mon…
32/
"Thinking in Bets" by @AnnieDuke is also an excellent resource on cultivating probabilistic thinking, and using it to make good decisions in situations where the outcome depends on chance events.
amazon.com/Thinking-Bets-…
"Thinking in Bets" by @AnnieDuke is also an excellent resource on cultivating probabilistic thinking, and using it to make good decisions in situations where the outcome depends on chance events.
amazon.com/Thinking-Bets-…
33/
Ted Seides (@tseides) has a wonderful podcast -- Capital Allocators -- where he's interviewed @AnnieDuke several times. You may want to listen to these episodes before reading the book.
Here's the latest one: capitalallocatorspodcast.com/2020/09/13/duk…
Ted Seides (@tseides) has a wonderful podcast -- Capital Allocators -- where he's interviewed @AnnieDuke several times. You may want to listen to these episodes before reading the book.
Here's the latest one: capitalallocatorspodcast.com/2020/09/13/duk…
34/
I know that it's a long tail, low probability event that you're still with me.
But if you are, I truly appreciate it.
Thanks for reading. Enjoy your weekend!
/End
I know that it's a long tail, low probability event that you're still with me.
But if you are, I truly appreciate it.
Thanks for reading. Enjoy your weekend!
/End
• • •
Missing some Tweet in this thread? You can try to
force a refresh