Lo prometido es deuda, o eso dicen, y una Grima siempre paga sus deudas.
Así que, con unos días de retraso respecto a lo previsto, os voy a contar cómo construir un fractal muy especial: el fractal de Fibonacci.
Así que, con unos días de retraso respecto a lo previsto, os voy a contar cómo construir un fractal muy especial: el fractal de Fibonacci.
https://twitter.com/ClaraGrima/status/1316147398041899008
Dedicado a todos los que me habláis con cariño y me animáis cuando estoy triste, asustada o desanimada.
Allá vamos :)
Allá vamos :)
La idea de escribir este hilo se me ocurrió el martes 13 de octubre del año de la pandemia.
Alguna gente, mucha, se estaba quejando (o asustando) en esta red social (y supongo que en otras) con la superstición asociada a los martes 13 en nuestra tradición.
Alguna gente, mucha, se estaba quejando (o asustando) en esta red social (y supongo que en otras) con la superstición asociada a los martes 13 en nuestra tradición.
Situación que aproveché para reivindicar que el 13 era un número precioso que, entre otras maravillas (es un primo pitagórico [13= 2^2 + 3^2]), aparecía en la sucesión de Fibonacci.
¿Qué es la sucesión de Fibonacci? Pues una sucesión que describió Fibonacci :)
¿Qué es la sucesión de Fibonacci? Pues una sucesión que describió Fibonacci :)
Ahora, en serio, Fibonacci, cuyo verdadero nombre era Leonardo de Pisa, fue un matemático italiano muy famoso y brillante que, entre otras cosas, planteó el siguiente pasatiempo.
Vamos a criar conejos.
Vamos a criar conejos.
Cada conejo tarda un mes en llegar a su edad fértil. Cada pareja de conejos en edad fértil puede parir a una pareja de conejitos cada mes.
Si comenzamos con una pareja de conejos bebés (les falta un mes para ser fértiles), ¿cuántas parejas de conejos tendremos al cabo de, por ejemplo, un año?
Vamos a calcularlo.
Vamos a calcularlo.
Después del primer mes, seguiremos teniendo sólo una pareja de conejos, pero ya fértiles, porque habrá pasado el tiempo necesario para su maduración.Les ponemos una etiqueta con un número 1 para identificarlos: 

¿Qué pasará al cabo de un mes?
Sólo la pareja 1 podrá tener conejitos, la pareja 2 estará creciendo hasta llegar a la edad fértil. A la nueva pareja de hijos de la pareja 1, les ponemos la etiqueta 3. Ya tenemos 3 parejas de conejos :)
Sólo la pareja 1 podrá tener conejitos, la pareja 2 estará creciendo hasta llegar a la edad fértil. A la nueva pareja de hijos de la pareja 1, les ponemos la etiqueta 3. Ya tenemos 3 parejas de conejos :)

Al mes siguiente, las parejas 1 y 2 tendrán nuevas crias y la pareja 3, habrá crecido
Tendríamos 5 parejas, a los nuevos hijos de 1 y 2 los etiquetamos con 4 y 5.
Tendríamos 5 parejas, a los nuevos hijos de 1 y 2 los etiquetamos con 4 y 5.
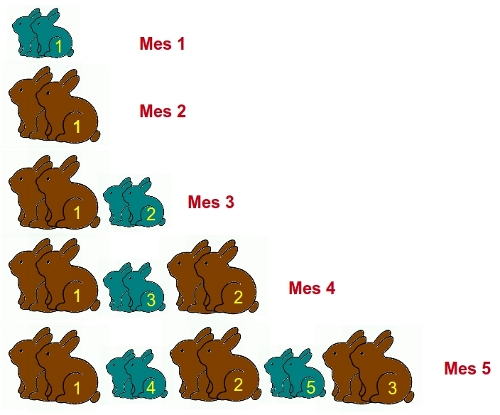
Un mes más tarde, habrá que añadir 3 nuevas parejas de conejos. Las crías de las 3 parejas adultas que teníamos. Las parejas 4 y 5 han destinado ese mes a madurar. Teníamos 5, más 3, ya tenemos 8 parejas de conejos. 

De esas 8 parejas solo 5 son adultas por lo que al mes siguiente tendremos 5 nuevas parejas de crías (las otras 3, hasta 8, han estado madurando). Ya tenemos, ¡sí!, 13 parejas =) 

Cada mes que pasa, tendremos que sumar tantas parejitas de bebés nuevas como parejas adultas tengamos, y ¿cuántas parejas adultas tenemos?
Eso es, exactamente el número total de parejas que teníamos el mes anterior. Y por lo tanto, al siguiente mes tendríamos 13 + 8, la suma de los dos meses anteriores. :)
Así se construye la sucesión de Fibonacci: cada término nuevo se calcula como la suma de los dos anteriores.
Así se construye la sucesión de Fibonacci: cada término nuevo se calcula como la suma de los dos anteriores.
Nota: se trata de un pasatiempo matemático.
Lo digo por si a alguien le hiere su sensibilidad el apareamiento entre hermanos en esta historia.
Lo digo por si a alguien le hiere su sensibilidad el apareamiento entre hermanos en esta historia.
¿Por qué es tan famosa esta sucesión tan simple? Fibonacci incluyó este pasatiempo en su libro “Liber Abaci” y en aquella época (año 1202) esta pasó sin pena ni gloria. 

Por cierto, fue ese libro de aritmética el que introdujo la numeración indoarábiga que hoy conocemos y pudimos, por fin, pasar del sistema de numeración romano que, prima, serían muy buenos construyendo acueductos pero de aritmética regular ná más.
Sigo. Resulta que, allá por 1877, un matemático francés, Édouard Lucas, se encontró la sucesión en el “Liber Abaci” y se puso a estudiarla como si no hubiese un mañana. Este señor, por cierto, inventó el juego de las Torres de Hanoi que es chulísimo también. 

Pero, a lo que vamos, fue don Édouard quién rescató nuestra secuencia y publicó una serie de estudios sobre la misma. Fue él quien la denominó “la sucesión de Fibonacci”.
A partir de ahí fueron surgiendo multitud de estudios matemáticos sobre la misma y se descubrieron numerosas e inesperadas propiedades de esta.
Ya te digo, hasta nació (en 1963) una revista dedicada exclusivamente a ella: “The Fibonacci quarterly”. Aquí podéis descargar todos los números, el último de agosto de 2020: fq.math.ca/list-of-issues…
Ni pandemia, ni pandemio.
Aquí se publica sobre Fibonacci con virus y sin virus. Vamos, hombre.
Aquí se publica sobre Fibonacci con virus y sin virus. Vamos, hombre.
Pues bien, aparte de las propiedades matemáticas que, como veis, siguen dando trabajo, lo llamativo de la sucesión de Fibonacci es que, además, está presente en muchos ¡fenómenos naturales!
¿Cómo os quedáis?
¿Cómo os quedáis?
Sí, de verdad. Una sucesión que sale de un pasatiempo aparece cuando menos te lo esperas en tol medio del campo. Por ejemplo, la podemos encontrar en el número de pétalos de las flores. La mayoría tiene 3 (lirios), 5 (parnassia), 8 (cosmos), 13 (algunas margaritas)... 

Pero, bueno, esto de las flores se lo preguntáis mejor a @bioamara que sabe más que nadie del tema :)
Podéis buscar en Google sobre la sucesión de Fibonacci y enontraréis un montón de cosas muy interesantes.
Y ahora sí. Vamos a construir el fractal de Fibonacci :)
Podéis buscar en Google sobre la sucesión de Fibonacci y enontraréis un montón de cosas muy interesantes.
Y ahora sí. Vamos a construir el fractal de Fibonacci :)
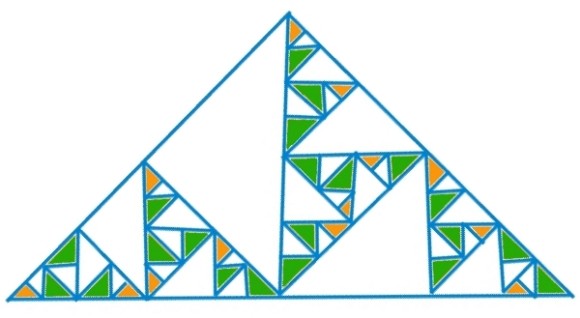
Para ello necesitamos un triángulo rectángulo, con un ángulo recto, isósceles, con dos lados iguales. A ese triángulo, vamos a ir borrándole trocitos, con el método que os voy a proponer. 

Trazamos la altura desde el ángulo recto en este triángulo. Obtenemos dos triángulos iguales. En uno de ellos, hacemos lo mismo. Tendremos dos mitades de ese triángulo más pequeño. Pues bien, borramos una de ellas. Así: 

Ahora, de los triángulos que nos quedan (en naranja) elegimos el de mayor área, lo pintamos, por ejemplo, de verde. 

Repetimos la operación sobre el triángulo verde: primero la altura desde el ángulo recto, luego en una de las dos mitades y borramos uno de los triángulos pequeñitos. 

Sobre esos triángulos verdes, ya sabéis, pintamos la altura desde el ángulo recto, luego en una de las mitades y borramos uno de los dos triangulitos. 

¿Cuántos triángulos tienen ahora mayor área? Eso es, 3. Huy, empezamos con 1 triángulo verde, luego 1, después 2, ahora 3… 

Vamos a pintar los 3 grandes en verde y le volvemos a robar un trocito con el mismo método y fijaos cuántos triángulos con el mayor área tenemos en el siguiente paso de la construcción. 

¡5! Al robar de nuevo un trocito a los 5 triángulos verdes cómo os he contado, nos quedan unos nuevos triángulos más grandes que serán en total… 

Hay, madre, que son 8… ¿Lo veis? 1, 1, 2, 3, 5, 8,... Esto huele a sucesión de Fibonacci que tira de espaldas.
¿Cuántos triángulos de mayor área (los que pintamos de verde) saldrán si repetimos la jugada en estos 8 triángulos?
¿Cuántos triángulos de mayor área (los que pintamos de verde) saldrán si repetimos la jugada en estos 8 triángulos?

Vamos a ver cómo queda, pintando sólo los triángulos que nos quedan, eliminando las líneas que sobran.
Monísimo, ¿no? =)
Monísimo, ¿no? =)

Podríamos repetir este proceso indefinidamente, hasta el infinito, y seguiríamos encontrando la sucesión de Fibonacci.
Sí, podéis llorar de emoción, yo también lloré cuando lo descubrí :___)
Sí, podéis llorar de emoción, yo también lloré cuando lo descubrí :___)
No se vayan todavía, aún hay más.
Vamos a colorear los trozos que le hemos robado, usando el mismo color cuando los triángulos borrados tienen el mismo área, a ver qué pasa…¿cuántos hay del mismo color?
Vamos a colorear los trozos que le hemos robado, usando el mismo color cuando los triángulos borrados tienen el mismo área, a ver qué pasa…¿cuántos hay del mismo color?

Aquí estoy llorando como una niña chica ante tanta belleza y eso que lo estoy contando yo...
Ea, pues ya tenéis entretenimiento para el fin de semana. En casita, que es donde mejor podéis estar en medio de una pandemia mundial :)
El Fractal de Fibonacci es también conocido como el Racimo de Grossman puesto que fue George W. Grossman el que lo describió en 1997. Si queréis ver el artículo en el que lo describe y publicado por Jounal of Mathematics and the Arts lo podéis ver aquí:
fq.math.ca/Scanned/35-3/g…
fq.math.ca/Scanned/35-3/g…
Si os encontráis con fuerzas tenéis este juego, el juego de Wythoff, en el que también se han escondido los conejos de Fibonacci.
Sigue al conejo blanco ;-)
mati.naukas.com/2018/04/14/sig…
Sigue al conejo blanco ;-)
mati.naukas.com/2018/04/14/sig…
Y, hablando de conejos, qué tarde es. Me voy, me voy, ¡me voy!
Espero que mi querida @farmagemma se lo cuente a Nico para que pueda presumir en el cole de lo que le gustan las matemáticas :)
Y nada más. Sigan con sus vidas, cuídense del virus que está por todas partes y sean muy felices.
• • •
Missing some Tweet in this thread? You can try to
force a refresh