Thread by @HygieneMentale

Je vous propose un petit exercice de pensée critique.

Imaginons que vous n'ayez absolument aucune idée apriori de la fiabilité de ce train.

Vous l'empruntez 15 fois,
et il arrive en retard 15 fois.

Quel est a votre avis la proportion habituelle de train en retard ?

Cet exercice est inspiré de l'excellente vidéo de @TroncheBiais sur la "Généralisation Abusive".


En s'entrainant un peu a manier les statistiques il me semble qu'il est possible de quantifier a quel point une généralisation est "abusive" ou pas.

_______________________________________

Voici ci-dessous quelques réflexions sur cette difficile question.

Le chiffre recherché est le pourcentage réel de trains qui arrive en retard en moyenne ces dernières année.

Ce chiffre est donc compris entre 0% et 100%.

Mais ce chiffre on ne le connais pas, on ne peut que essayer de le deviner.

Ou plus exactement on peut essayer d'estimer de façon subjective notre degré de croyance sur la proportion de train en retard, en se basant uniquement sur nos observations personnelles.

Pour chaque chiffre possible j'ai une croyance personnelle sur sa plausibilité. (vous être pas obligé d'avoir les mêmes)

Sur les graphs ci dessous, les hauteurs des courbes représentent mes plausibilités subjectives.

Très haut, c'est probable
Très bas c'est improbable

0) Mon Apriori (avant le premier trajet)

Ici on imagine qu'on a aucun apriori sur la proportion de train en retard.

Ca peut tout aussi bien être 0%, 12%, 99%, 100%.
Je représente ca par une courbe plate.

On appelle ca un apriori non-informatif.

1) Mon 1er train arrive en retard.

C'est donc impossible que 0% des trains arrivent en retard.
Je modifie un peu mon apriori.
Ma distribution de crédence est maintenant linéaire.

2) 2 trains = 2 retard

C'est toujours possible que 50% des trains arrivent en retard, j'aurais juste pas eu de chance.

Je modifie encore un peu ma distribution de crédence.
(en fait c'est juste le carré de la précédente)

3) 15 train = 15 retard

A chaque train que je prends je met a jour mes crédences.
Il me suffit de multiplier ma crédence précédente par la fonction linéaire que on a vu au premier train.

Maintenant j'ai réellement des raisons de penser que tous les trains arrivent en retard.

Pour les plus matheux d'entre vous, il s'agit tout simplement d'une fonction BETA(0 ; 15)

BETA (a l'heure ; en retard)

fr.wikipedia.org/wiki/Fonction_…
(Rassurez-vous, c'est beaucoup moins compliqué que ca en a l'air)

Bref, avec 15 retard sur 15 trajet, je suis plutôt justifié a penser que TOUS leurs trains arrivent en retard.

Ce n'est pas vraiment abusif de "généraliser" mes 15 resultats en une règle générale.

Mais en vérité si il s'agit de notre monde a nous (et non plus un monde fictif dont on ne sait rien) , j'ai bien évidemment un apriori très fort.

J'ai déjà pris le train souvent, mes proches aussi, je suis les infos, etc.

Ce n'est pas une courbe plate. 😁👆

Je peux même faire quelques recherches pour avoir une opinion encore plus forte : toutes les statistiques de retards de la SNCF sont rendu publique chaque année.
data.gouv.fr/fr/datasets/re…

Malgré ma confiance toute relative en la fiabilité des données officielles, je pense malgré tout que la proportion des trains SNCF en retard (>5mn) se situe aux alentours de 15%.

La distribution est très étroite car il y a ici beaucoup de données (~15000 trains/jours !)

Si maintenant je prends 15 fois le train, et que j'ai 15 retard, j'en conclue que j'ai VRAIMENT pas eu de bol, pas que 100% des trains SNCF ont des retard.

Ma crédence se contente de se déplacer un peu!.
Ces 15 retards me remettent un peu en question.

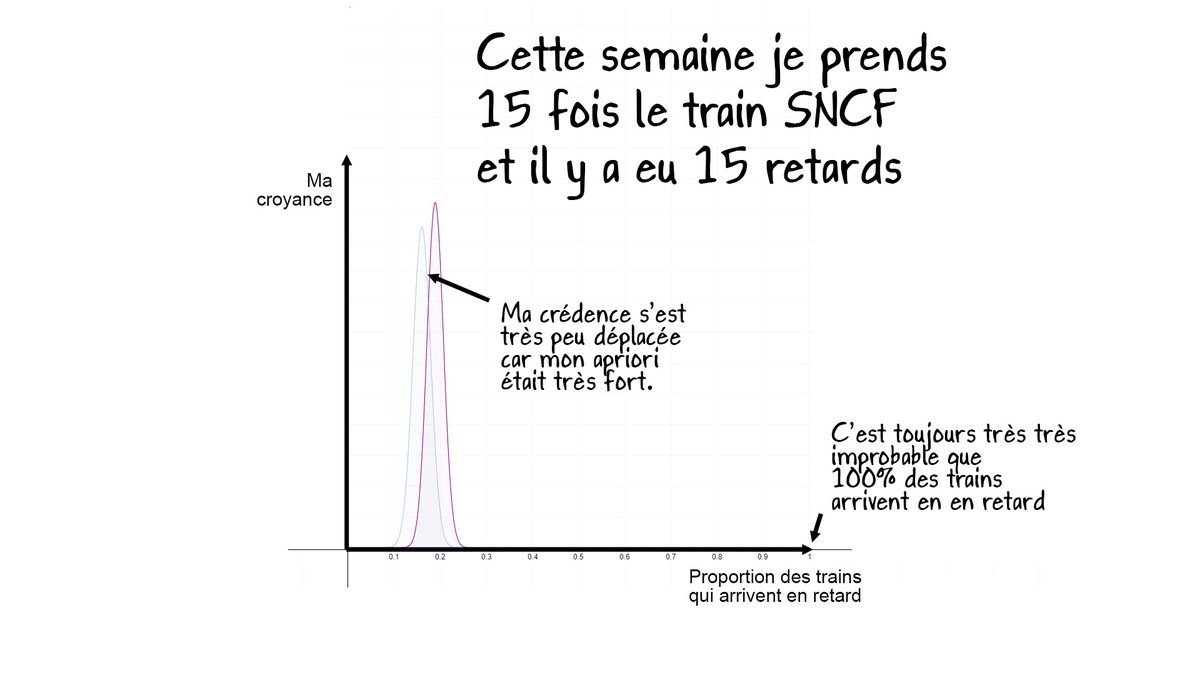
CONCLUSION :
Conclure que 100% des trains arrive en retard au prétexte que j'ai eu 15 retard sur 15 trajet n'est pas une généralisation abusive en soi.

Ca dépends fortement de l'apriori.

Ce n'est une généralisation abusive que si on avait un apriori fort.

#BAYES

GENERALISATION-CEPTION :

Beaucoup de nos erreurs de raisonnement viennent du fait que l'on oublie de prendre en compte nos aprioris.

Même les sceptiques aguerris négligent souvent de préciser que leur conclusions dépendent fortement de leurs apriori.

NOTE :
J'ai calculé mes graphs avec geogebra.org
Logicien libre, gratuit, utilisable directement enligne.

J'ai volontairement caché les maths qu'il y a derrière ces courbes, mais c'est assez velu. 😅

Pour continuer voici un autre thread intéressant sur ce sujet. par @LaBile_philo .

https://twitter.com/LaBile_philo/status/1334258493474398210

Ou encore cet excellent thread par @Bunker_D_ .

https://twitter.com/Bunker_D_/status/1334608974142971907