Thread by @andrewgwils

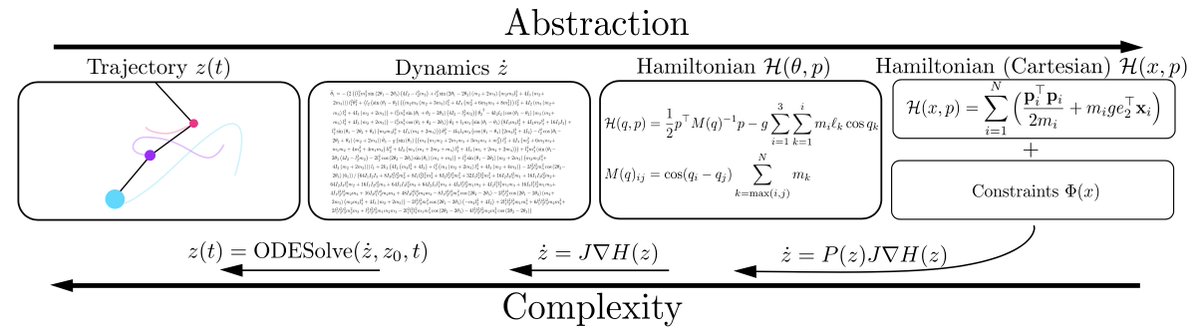
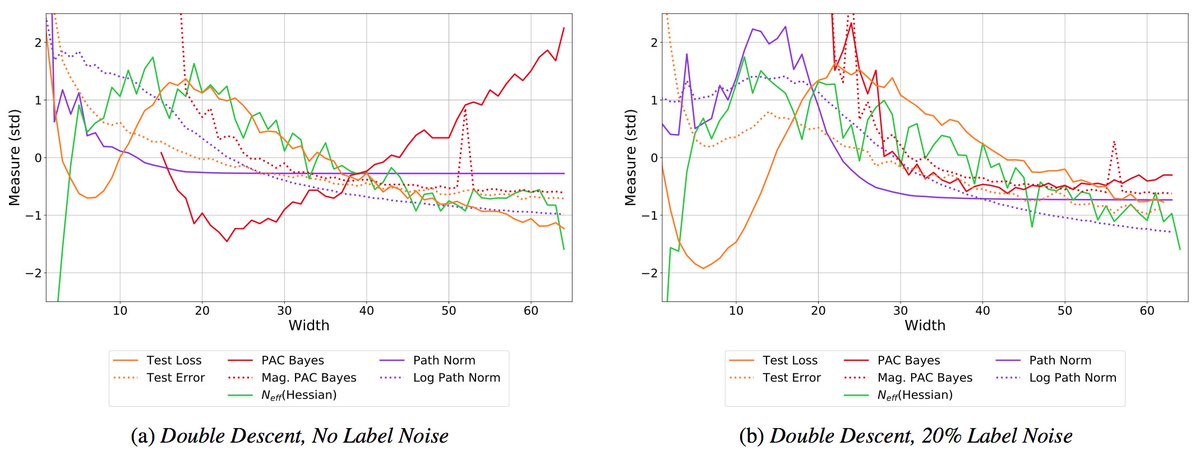
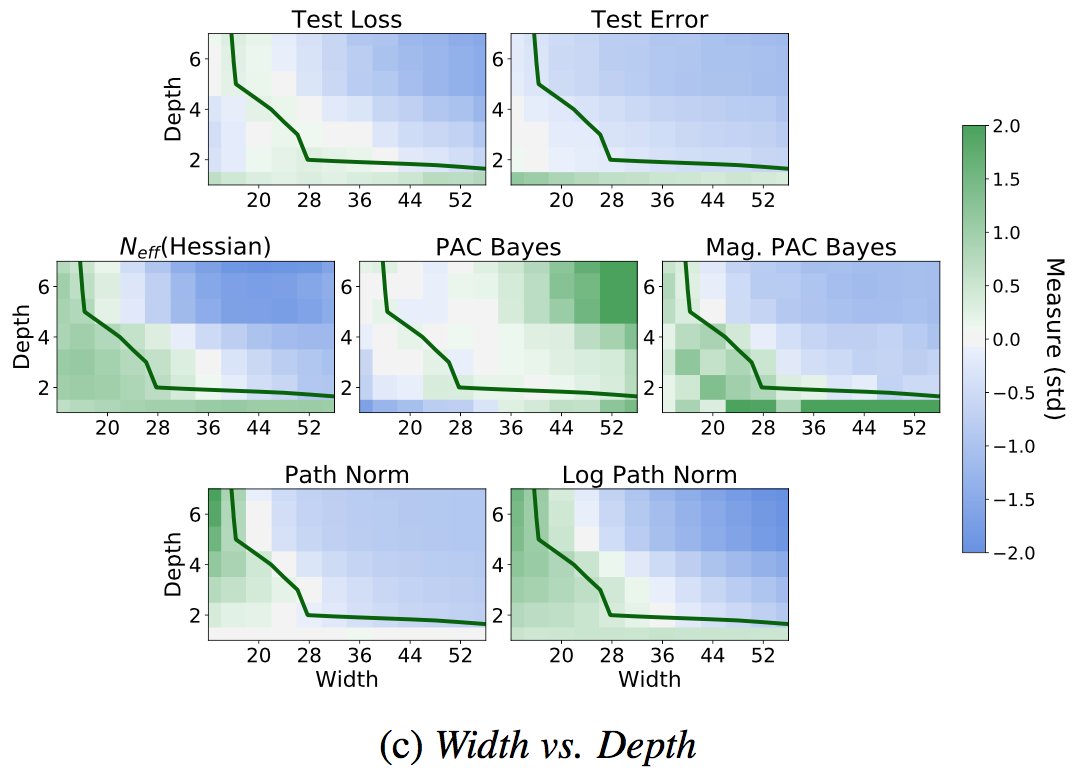
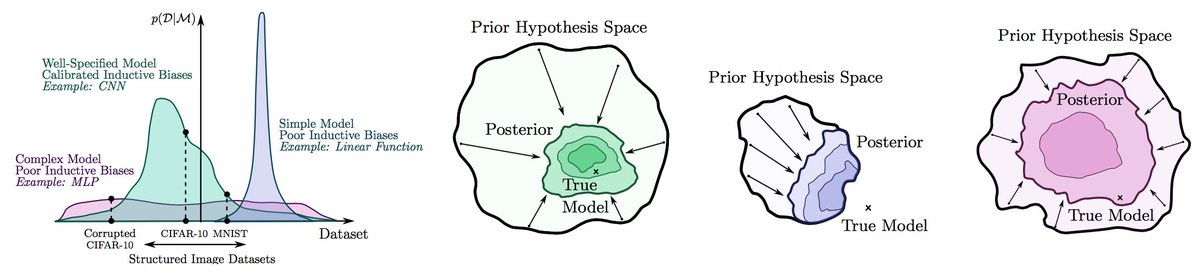
In practice, standard "deep ensembles" of independently trained models provides a relatively compelling Bayesian model average. This point is often overlooked because we are used to viewing Bayesian methods as sampling from some (approximate) posterior... 1/10

...to form a model average, via simple Monte Carlo. But if we instead directly consider what we ultimately want to compute, the integral corresponding to the marginal predictive distribution (the predictive distribution not conditioning on weights)... 2/10

...then deep ensembles are in practice a _better_ approximation to the Bayesian model average than methods that are conventionally accepted as Bayesian (such as Laplace, variational methods with a Gaussian posterior, etc.). 3/10

This isn't just an issue of semantics, but a practically and conceptually important realization. It makes sense to view the Bayesian integration problem in DL as an active learning problem under severe computational constraints, and that's what deep ensembles are doing. 4/10

If you have to approximate p(y|D) = \int p(y|w) p(w|D) dw by querying a handful of points in weight space, you wouldn't even want exact samples from the posterior p(w|D)! You would care about getting high density (and typical) points with functional variability. 5/10

Would these points be equally weighted in a BMA? Well, is the posterior density the same? Yes, typically. And do ensembles even have to be equally weighted? No. 6/10

Do BMAs for neural networks contain an infinite number of points? If we do the integral exactly, yes. But in practice, not even close! In practice, conventional deep BNN methods are taking about a dozen samples from a unimodal approximate posterior. 7/10

Under standard computational constraints, deep ensembles will get you a better approximation of the BMA than most conventional Bayesian approaches. You could do better if you ran a good MCMC method for a really really long time. 8/10

Are ensembles and Bayesian methods always the same? No. Ensembling methods can enrich the hypothesis space, whereas Bayesian methods assume one correct hypothesis. But this distinction doesn’t apply for "deep ensembles", which don't enrich the hypothesis space. 9/10

We discuss these topics, and many others, in “Bayesian Deep Learning and a Probabilistic Perspective of Generalization" (arxiv.org/pdf/2002.08791…). See you at NeurIPS on Th! neurips.cc/virtual/2020/p…

10/10