Encouraging! #AppleM1 Silicon (MBA) smokes my 2017 MBP15" i7 on #rstats #tidverse tidymodels hotel example, random forests (last fit 100 trees). Experimental arm-R build = extra speedup. Thanks @fxcoudert for gfortran build & @juliasilge @topepos + team for the nice API + DOC. 
And it’s wonderful to see that essential R packages are working on the M1 platform.
Another implication might be that 4 cores are a good default for parallel processing with this configuration. The original tidymodels example would select 8 cores here. tidymodels.org/start/case-stu…
If you are interested in the benchmark, here is the code I used. Computing: gist.github.com/dengemann/a9e4…
Plotting:
gist.github.com/dengemann/4759…
Plotting:
gist.github.com/dengemann/4759…
Update including i9 MBP 16" results; x-axis jitter removed for clarity
Update: Using #Python I find comparable results when using the random forests from scikit-learn on the same dataset. #AppleM1 is systematically faster + the native ARM build makes a difference. Interestingly, the Intel Mac seems still faster with basic linear algebra (next tweet)
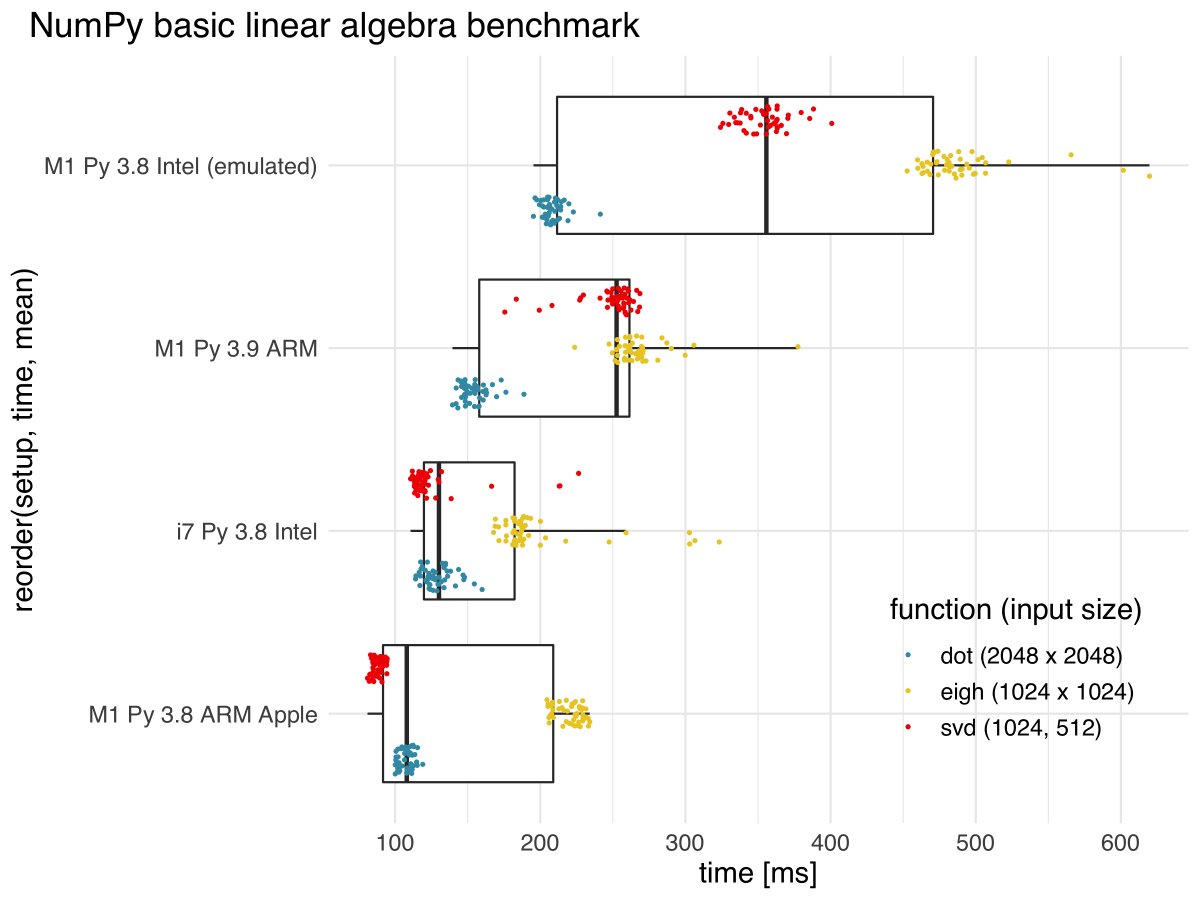
Benchmarking matrix multiplication, SVD, and eigen decomposition the i5 Intel from 2017 was fastest #NumPy.(gist.github.com/dengemann/03a0…) obviously this is not what matters for random forests. Note that M1 native (yellow) plays in the league as i5 and these are only the first builds.
Correction: It’s of course i7, not i5 – a misnomer. Still the same machine as in previous benchmarks.
As anticipated, the story with #NumPy on #AppleM1 is not quite over. With NumPy optimised for ARM via #Apple #TensorFlow M1 can beat the i7 on matrix multiplication and SVD! Excited to see what's yet to come. cc @numpy_team @PyData
• • •
Missing some Tweet in this thread? You can try to
force a refresh
