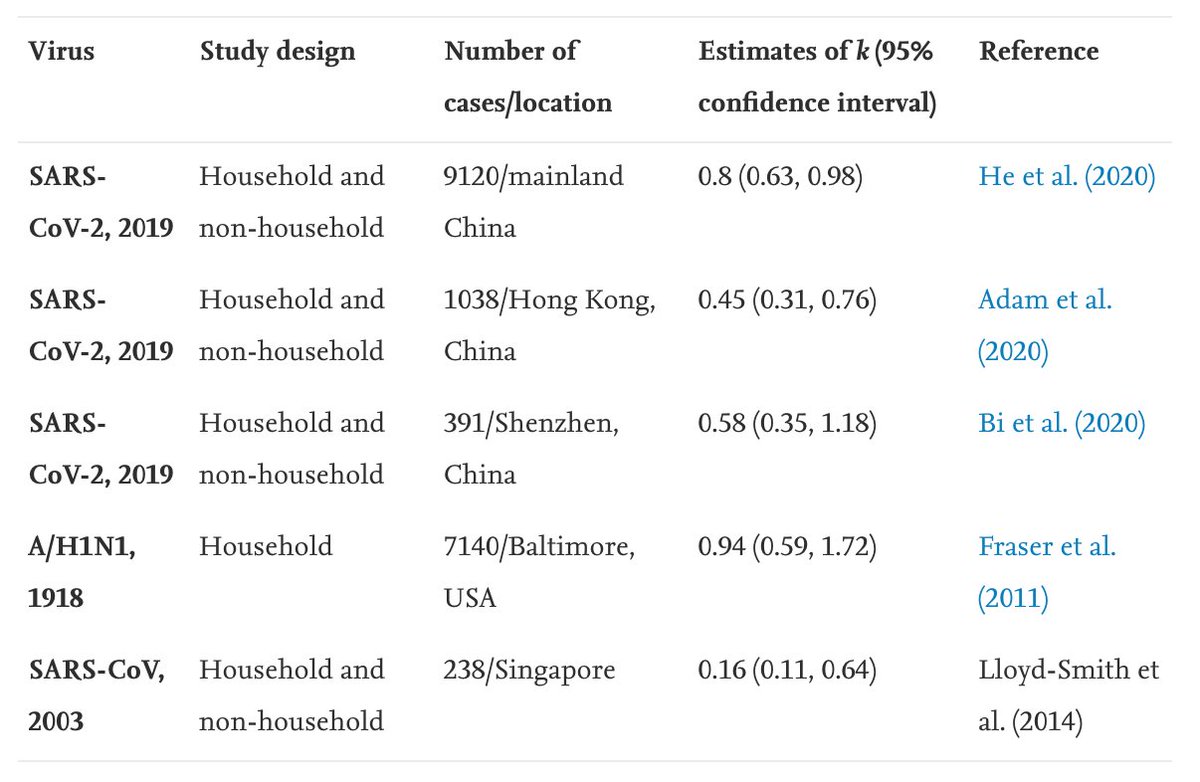
A few people have correctly pointed out that theoretical tradeoff below could be different in longer term if no vaccine available. Given vaccine on horizon in UK, I focused on timescale of weeks because that will be a crucial period. But let's explore some broader scenarios... 1/
https://twitter.com/AdamJKucharski/status/1343567425107881986
Suppose control measures can get R=0.6. We can calculate expected total number of infections = N/(1-R), where N is current infections. So if 10k initial infections, would expect 25k overall, but 100k if virus 50% more transmissible (i.e. R=0.9). 2/
https://twitter.com/AdamJKucharski/status/1324662478316408833?s=20
Next, suppose control can get R=0.8. In this scenario, 50% increase in transmission (R=1.2) tips epidemic into exponential growth. So we go from declining outbreak to one that sweeps uncontrolled through population. Hence 50% increase could mean many many fold more infections. 3/
Finally, suppose R=1.2. If we use a simple SIR model, we can calculate final epidemic size (F) by solving log(1-F) = R x F . So if R=1.2, this would mean 31% infected. If R=1.2x1.5 = 1.8 (i.e. 50% more transmissible), we'd expect 73% infected. 4/
These are simple illustrative examples, but key point is that small differences in transmissibility are particularly important when we're near the epidemic threshold (i.e. R=1) - which is where many European countries currently are. 5/5
• • •
Missing some Tweet in this thread? You can try to
force a refresh