
#統計
⓪確率変数Xの分布は期待値E[f(X)]達(fを動かす)から決まる。
①特性函数についてなら添付画像1の通り。単なるFourier解析。
②中心極限定理には、モーメント母函数や特性函数を使わずに、Taylorの定理のみを使う初等的な証明があります(概略は添付画像2)。この証明法はもっと普及するべき。

⓪確率変数Xの分布は期待値E[f(X)]達(fを動かす)から決まる。
①特性函数についてなら添付画像1の通り。単なるFourier解析。
②中心極限定理には、モーメント母函数や特性函数を使わずに、Taylorの定理のみを使う初等的な証明があります(概略は添付画像2)。この証明法はもっと普及するべき。
https://twitter.com/lively_metro/status/1345951061865951232


#統計 学部レベルの統計学入門の教科書の多くが、なぜか、(Fourier解析の知識を要求する)モーメント母函数や特性函数を経由する中心極限定理の証明またはその概略をコピー&ペーストのごとく載せているのは不思議なことです。
教科書の著者達が集団でコピペしまくっている疑いがあります。
教科書の著者達が集団でコピペしまくっている疑いがあります。
#数楽 Taylorの定理の証明も数十年以上コピペが蔓延している疑いが強い。
Cⁿ級を仮定すれば、n階の導函数f^{(n)}(x)をaからxまで積分することをn回繰り返すだけでTaylorの定理が得られる。
g(x) = g(a) + ∫_a^x g'(t)dt をn回使う。
Cⁿ級を仮定すれば、n階の導函数f^{(n)}(x)をaからxまで積分することをn回繰り返すだけでTaylorの定理が得られる。
g(x) = g(a) + ∫_a^x g'(t)dt をn回使う。
https://twitter.com/genkuroki/status/1295512877248311296
#統計 訂正: X_1,…,X_n, Y_1,…,Y_nの独立性も仮定していることを書くのを忘れていた。ひどいので訂正版を出しておきます。
本質的にTaylorの定理しか使わない中心極限定理の証明の概略。
1/√nのオーダーの量の3乗をn個足した結果は1/√nのオーダーでn→∞で0になります。たったそれだけのこと!
本質的にTaylorの定理しか使わない中心極限定理の証明の概略。
1/√nのオーダーの量の3乗をn個足した結果は1/√nのオーダーでn→∞で0になります。たったそれだけのこと!
https://twitter.com/genkuroki/status/1349949346406514688

#数楽 f(X) = exp(itX) (t∈ℝ)の全体について期待値 E[f(X)] が分かっていれば、Fourier解析によってそのようなf(X)の重ね合わせでほとんどすべての関数が得られるので、X の分布も一意に特徴付けられると考えられるわけです。
これは非常に健全な直観で実際にうまく行きます。
これは非常に健全な直観で実際にうまく行きます。
#数楽 閉区間上の任意の連続函数は多項式函数で一様に幾らでも近似できるので、「E[Xᵏ]型の期待値(モーメント)達で X の分布が特徴付けられるのではないか?」と予想するのは自然です(モーメント問題)。
しかし、対数正規分布のような有名な分布が反例になっているので、一般には正しくないです。
しかし、対数正規分布のような有名な分布が反例になっているので、一般には正しくないです。
#数楽 一般にはダメであることは全然ダメであることを意味せず、かなり弱い一般的な仮定を追加すれば、E[Xᵏ]型の期待値(モーメント)達から確率変数 X の分布が一意に決まることを示せます。
#数楽
* 確率変数 X の分布は十分に沢山の函数 f(X) の期待値 E[f(X)] の情報で一意に特徴付けられる。(これは認めて使って良いと思う)
* f(X) = exp(itX) (t∈ℝ)型の f(X) の期待値達(特性函数)から X の分布は一意に特徴付けられる。
* 確率変数 X の分布は十分に沢山の函数 f(X) の期待値 E[f(X)] の情報で一意に特徴付けられる。(これは認めて使って良いと思う)
* f(X) = exp(itX) (t∈ℝ)型の f(X) の期待値達(特性函数)から X の分布は一意に特徴付けられる。
#数楽
* f(X) = Xᵏ (k=0,1,2,…)の期待値(モーメント)だけから X の分布が一意に決まるという主張は一般的には成立していないが、広く成立している。
問題を少し一般化した方が感覚がつかみやすいと思う。
おまけ: 中心極限定理には本質的にTaylorの定理のみを使う易しい証明がある。
* f(X) = Xᵏ (k=0,1,2,…)の期待値(モーメント)だけから X の分布が一意に決まるという主張は一般的には成立していないが、広く成立している。
問題を少し一般化した方が感覚がつかみやすいと思う。
おまけ: 中心極限定理には本質的にTaylorの定理のみを使う易しい証明がある。
#統計 モーメント母函数や特性函数を使う中心極限定理の証明でも、Taylorの定理を使う証明でも、中心極限定理の誤差の主要項の大きさは E[X]=0, E[X²]=1 のとき、E[X³]の大きさで決まります。
E[X]=μ, E[(X-μ)²]=σ² の場合には E[(X-μ)³]/σ³ の大きさで決まる。
E[X]=μ, E[(X-μ)²]=σ² の場合には E[(X-μ)³]/σ³ の大きさで決まる。

#統計 だから、中心極限定理の収束の遅さの意味での正規分布との違いの大きさの指標の1つとして、E[(X-μ)³]/σ³ の推定値の絶対値を使えると考えられます。(X が正規分布に従えば E[(X-μ)³]/σ³ = 0 になる。左右対称でも E[(X-μ)³]/σ³ = 0 となる。左右対称でなくなると ≠ 0 になる。)
#統計 以上のような中心極限定理の収束の仕方に踏み込んだ議論を知っていれば、「正規分布モデルを使った推測において、真の分布が正規分布でなくても中心極限定理が効けば誤差が小さくなるとき、サンプルの分布が左右対称なら誤差が小さくなっている可能性が高くなる」というようなことが言えます。
#統計 注意:「最小二乗法=残差を正規分布でモデル化した場合の最尤法」なので、最小二乗法の場合には残差の様子を見る。
#統計 統計学は【お墨付き】を得る方法ではなく、確率的に勝ち目を増やす方法なので、データが示唆するリスクに注意することが大事なんだと思う。
何に注意するべきであるかは、各分野の専門知識と経験がないと分からない。
例えば数理統計学の知識だけあっても麻雀に統計学を適切に応用できない。
何に注意するべきであるかは、各分野の専門知識と経験がないと分からない。
例えば数理統計学の知識だけあっても麻雀に統計学を適切に応用できない。
#統計 中心極限定理の勉強法として
コンピュータで平均μ分散σ²の分布の長さnの(擬似)乱数列X_1,…,X_nをL組発生させて、((X_1-μ)+…+(X_n-μ))/√(nσ²)達のヒストグラムをプロットし、標準正規分布と比較する
という方法があります。
そのとき、
うまく行かない場合も探すこと
が大事です!
コンピュータで平均μ分散σ²の分布の長さnの(擬似)乱数列X_1,…,X_nをL組発生させて、((X_1-μ)+…+(X_n-μ))/√(nσ²)達のヒストグラムをプロットし、標準正規分布と比較する
という方法があります。
そのとき、
うまく行かない場合も探すこと
が大事です!
https://twitter.com/genkuroki/status/1350787173184802818
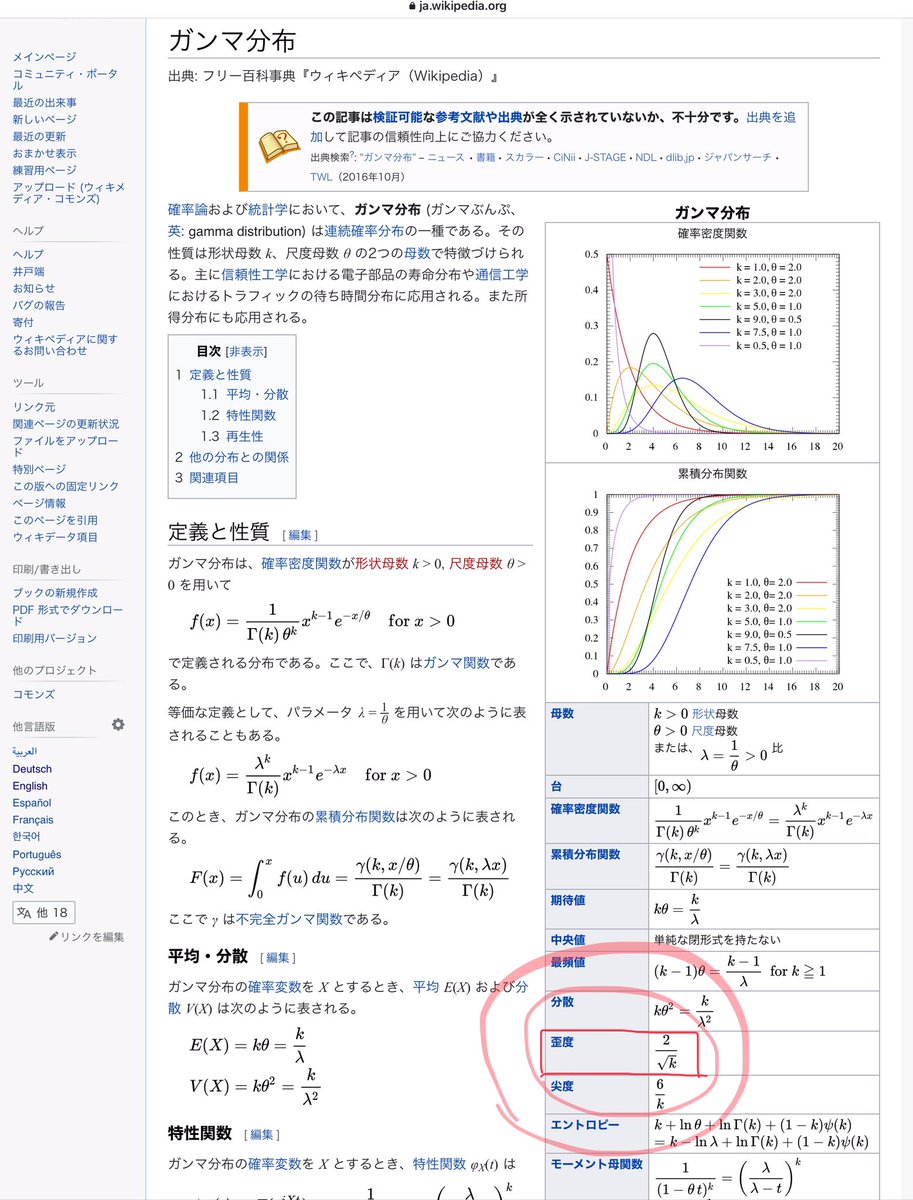
#統計
一般に左右対称な分布の歪度は0になる。
ベルヌイ分布Bernoulli(p)の歪度は(1-2p)/√(p(1-p))で、p≈0のとき歪度は1/√pで近似される。
ja.wikipedia.org/wiki/%E3%83%99…
ガンマ分布Gamma(α,θ)の歪度は2/√α
ja.wikipedia.org/wiki/%E3%82%AC…
確率分布についてはウィキペディアはかなり便利だと思います。

一般に左右対称な分布の歪度は0になる。
ベルヌイ分布Bernoulli(p)の歪度は(1-2p)/√(p(1-p))で、p≈0のとき歪度は1/√pで近似される。
ja.wikipedia.org/wiki/%E3%83%99…
ガンマ分布Gamma(α,θ)の歪度は2/√α
ja.wikipedia.org/wiki/%E3%82%AC…
確率分布についてはウィキペディアはかなり便利だと思います。

#統計 数学的に理想化された状況ではn→∞とできますが、現実にはそうできないので、有限のnでの様子について知っておく必要あり!
「理想化されていない数学的状況についても考えてみる」という発想ができれば、コンピュータの擬似乱数で中心極限定理の確認をしても「騙される可能性」が減ると思う。
「理想化されていない数学的状況についても考えてみる」という発想ができれば、コンピュータの擬似乱数で中心極限定理の確認をしても「騙される可能性」が減ると思う。
#統計 #Julia言語
コンピュータで0~1の一様乱数n個の和達のヒストグラムをプロットしてみる。
①n=3ですでにかなり正規分布っぽい。
②n=5なら正規分布にかなり近い。
③n=10ならほぼ完璧に正規分布!
「中心極限定理による近似は小さなnでもかなり良い!」と思ってしまうと騙されたことになる!


コンピュータで0~1の一様乱数n個の和達のヒストグラムをプロットしてみる。
①n=3ですでにかなり正規分布っぽい。
②n=5なら正規分布にかなり近い。
③n=10ならほぼ完璧に正規分布!
「中心極限定理による近似は小さなnでもかなり良い!」と思ってしまうと騙されたことになる!



#統計 「小さなnであっても中心極限定理による近似が相当に正確な場合もある」と理解できれば問題ないのですが、「中心極限定理による近似は小さなnでも常に悪くない」のように思ってしまうとまずいです。
コンピュータによるrand()の和の分布の実験が非常に印象的なので騙されないように注意!
コンピュータによるrand()の和の分布の実験が非常に印象的なので騙されないように注意!
#統計 しかし、一様分布の和rand()+rand()+rand()の分布を見る実験で強い印象受けて騙されかけるのは非常に良いことだと思います。「たった3つの和で正規分布っぽくなるのか!」と感動するのも良いこと。
沢山試行錯誤して「あれ?中心極限定理による近似が悪い!」と思う例に到達すると楽しい。
沢山試行錯誤して「あれ?中心極限定理による近似が悪い!」と思う例に到達すると楽しい。
#統計 #Julia言語
Gamma(0.1, 10)という極端に偏った分布の場合
①n = 10 では全然正規分布っぽくならない。
②n = 100 でも正規分布近似はよくない
③n = 1000 ならかなり正規分布に近い
④もとのGamma(0.1, 10)分布の様子



Gamma(0.1, 10)という極端に偏った分布の場合
①n = 10 では全然正規分布っぽくならない。
②n = 100 でも正規分布近似はよくない
③n = 1000 ならかなり正規分布に近い
④もとのGamma(0.1, 10)分布の様子




#統計
①n=100, p=0.3の場合の中心極限定理による正規分布近似の精度はかなり高い。
②n=100, p=0.03では正規分布近似の精度は低い。
③n=100, p=0.03でのPoisson分布近似はかなりよい。
pが0.5に近い場合の様子しか見ないと騙され易い。
正規分布近似以外にも良い近似の仕方がある場合がある。


①n=100, p=0.3の場合の中心極限定理による正規分布近似の精度はかなり高い。
②n=100, p=0.03では正規分布近似の精度は低い。
③n=100, p=0.03でのPoisson分布近似はかなりよい。
pが0.5に近い場合の様子しか見ないと騙され易い。
正規分布近似以外にも良い近似の仕方がある場合がある。



#Julia言語 以上で使ったコードは
nbviewer.jupyter.org/gist/genkuroki…
gist.github.com/genkuroki/a804…
からダウンロードできます。
nbviewer.jupyter.org/gist/genkuroki…
gist.github.com/genkuroki/a804…
からダウンロードできます。
#Julia言語 以上では、歪度 skewness に注目するという話をしましたが、中心極限定理による近似がうまく行かない場合を理解するにはもちろんそれだけでは不十分です。
(重要!コンピュータで実験する場合には必ず「近似がうまく行かない場合」も探すこと!これ、とても大事。個性を発揮しやすい分野)
(重要!コンピュータで実験する場合には必ず「近似がうまく行かない場合」も探すこと!これ、とても大事。個性を発揮しやすい分野)
#Julia言語 一般論によるnへの依存性の分析はn→∞の様子を見ている場合がどうしても多くなります。
n→∞での様子の分析がそのまま小さなnでも有効な場合があって、そういう場合があることの認識は応用上重要なのですが、「常にうまく行く」と思ってしまうのは危険です。
反例を作ることが重要。
n→∞での様子の分析がそのまま小さなnでも有効な場合があって、そういう場合があることの認識は応用上重要なのですが、「常にうまく行く」と思ってしまうのは危険です。
反例を作ることが重要。
#Julia言語 #数楽 #統計 例えば、小さな割合で極端な値を取る場合にある分布(外れ値を持つ分布)では、小さなnでの中心極限定理による近似はうまく行きません。
なぜならば、nを十分に大きくしないと、小さな割合でしか生じない極端な値の真の割合が分からないからです。
なぜならば、nを十分に大きくしないと、小さな割合でしか生じない極端な値の真の割合が分からないからです。
#統計 サンプルの様子を眺めてみたら、左右の対称性が極端に崩れていたり、外れ値が含まれているように見えるならば、中心極限定理による近似(による平均値の検定や推定)は危険です。
サンプルの様子を要約せずに眺めてみることはとても重要です。
サンプルの様子を要約せずに眺めてみることはとても重要です。
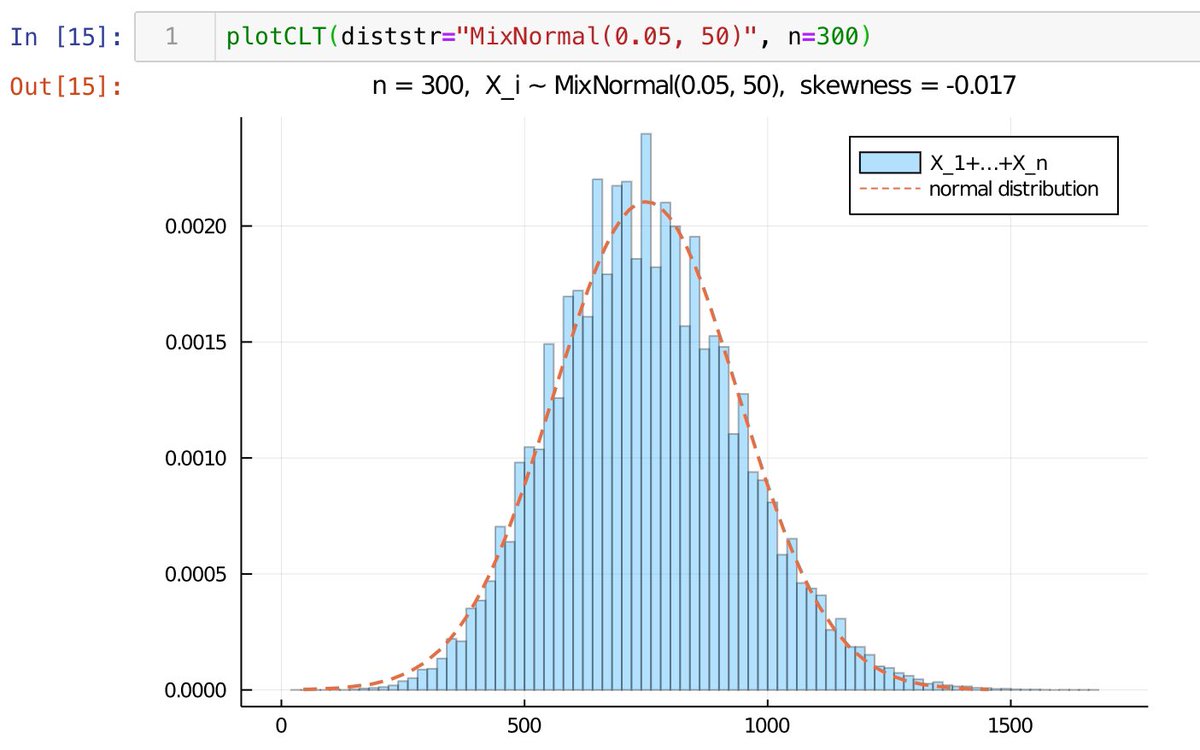
#統計 #Julia言語
極端に大きな値が5%含まれている混合正規分布に関する中心極限定理の効き方
①skewnessは小さい。
②n=30では正規分布から程遠い。
③n=100でもちょっとあれな感じ?
④n=1000ならかなり正規分布に近付いた?
本当は経験分布の累積確率分布函数をプロットするべき。



極端に大きな値が5%含まれている混合正規分布に関する中心極限定理の効き方
①skewnessは小さい。
②n=30では正規分布から程遠い。
③n=100でもちょっとあれな感じ?
④n=1000ならかなり正規分布に近付いた?
本当は経験分布の累積確率分布函数をプロットするべき。



#数楽 #統計 まとめ
* 中心極限定理の証明を眺めると、左右非対称な分布で中心極限定理による正規分布近似の精度が低くなりそうなことが分かり、コンピュータによる実験でも確認できる。
* 元の分布が外れ値を含む場合にも、小さなnでの中心極限定理による近似の精度は低くなりやすい。
* 中心極限定理の証明を眺めると、左右非対称な分布で中心極限定理による正規分布近似の精度が低くなりそうなことが分かり、コンピュータによる実験でも確認できる。
* 元の分布が外れ値を含む場合にも、小さなnでの中心極限定理による近似の精度は低くなりやすい。
#数楽 コンピュータで疑似乱数を発生させて、中心極限定理を数値的に確認する遊びをする場合には、中心極限定理による正規分布近似がうまく行かない例を色々作ると理解が深まります。
他にも各種の信頼区間やχ²検定やWelchのt検定などがうまく行かない例を作ることがとても大事だと思います。
他にも各種の信頼区間やχ²検定やWelchのt検定などがうまく行かない例を作ることがとても大事だと思います。
#統計 #数楽 統計学のような解析学の応用では、必ず近似を使った推論が使われます。
その近似がどれだけどのようにうまく行くかを知るためには、近似がうまく行かない場合についても知っておく必要があります。
表面だけではなく、裏面にも注意を払うことが重要。
裏面も十分に面白い。
その近似がどれだけどのようにうまく行くかを知るためには、近似がうまく行かない場合についても知っておく必要があります。
表面だけではなく、裏面にも注意を払うことが重要。
裏面も十分に面白い。
#統計 pが小さくてnが大きめの二項分布のポアソン分布による近似の証明には
lim_{n→∞}(1 + x/n)ⁿ = eˣ
が使われます。高校で習う極限
lim_{n→∞}(1 + 1/n)ⁿ = e
の一般化です。高校の段階でこの極限の収束の様子・近似の精度についても触れておくことができれば、色々都合がよいと思う。
lim_{n→∞}(1 + x/n)ⁿ = eˣ
が使われます。高校で習う極限
lim_{n→∞}(1 + 1/n)ⁿ = e
の一般化です。高校の段階でこの極限の収束の様子・近似の精度についても触れておくことができれば、色々都合がよいと思う。
https://twitter.com/genkuroki/status/1352777818560716800

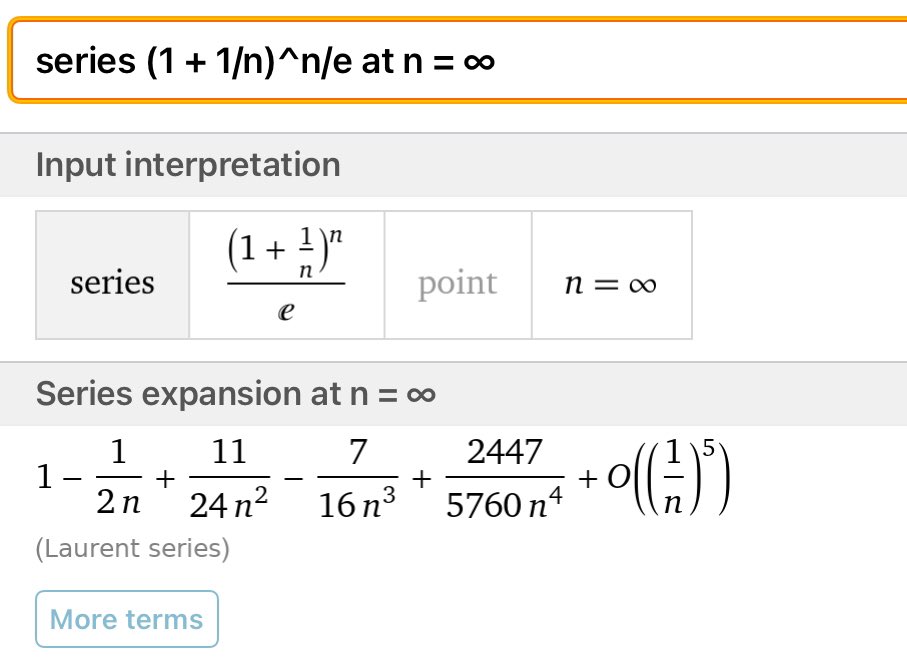
#数楽 (1 + 1/n)ⁿ や (1 + x/n)ⁿ が e や eˣ を大雑把にどの程度近似しているかはWolframAlphaで添付画像のように確認できます。
後者へのリンク↓
wolframalpha.com/input/?i=serie…
nが十分大きなとき、相対誤差は大雑把に、-1/(2n) (もしくは -x²/(2n))程度になります。nに反比例する。

後者へのリンク↓
wolframalpha.com/input/?i=serie…
nが十分大きなとき、相対誤差は大雑把に、-1/(2n) (もしくは -x²/(2n))程度になります。nに反比例する。

#数楽
(1 + x/n)ⁿ/eˣ = 1 - x²/(2n) + x³(3x+8)/(24n²) - …
の証明は h = 1/n とおいて、
(1/h)log(1 + xh) = x - x²h/2 + x³h²/3 - …
を
(1+x/n)ⁿ = (1+xh)^{1/h} = exp((1/h)log(1 + xh))
に代入して、h = 1/nについて展開すれば得られます。
logをとってから展開するのがミソです。
(1 + x/n)ⁿ/eˣ = 1 - x²/(2n) + x³(3x+8)/(24n²) - …
の証明は h = 1/n とおいて、
(1/h)log(1 + xh) = x - x²h/2 + x³h²/3 - …
を
(1+x/n)ⁿ = (1+xh)^{1/h} = exp((1/h)log(1 + xh))
に代入して、h = 1/nについて展開すれば得られます。
logをとってから展開するのがミソです。

#数楽 単に収束先しか分からない道具(ロピタルの類)よりも、収束の途中の様子の大雑把な様子も分かる道具(テイラー展開の類)の方が、「近似の精度」が問題になる実践的な状況では有用です。
高校の段階で「単に極限を求めるのではなく、収束の途中の様子も理解しようとする」としておくとよいと思う。
高校の段階で「単に極限を求めるのではなく、収束の途中の様子も理解しようとする」としておくとよいと思う。
#数楽 高校で「出された問題を解くのが数学。極限を求める問題では極限の値さえ求まればよい」というような貧しい考え方にさらに「高校で習ったこと以外を使ってはいけない」という大学入試においても無意味な縛り(クズそのもの)を合体させると、数学がくだらない分野だと誤解してしまうので要注意。
#数楽 高校で習う (1 + 1/n)ⁿ → e という極限の収束の様子(誤差の大きさ)の話は、二項分布のポアソン分布による近似のような現実世界を理解するための技術に直結している。
単なる極限の公式1つだけで幾らでも楽しめるし、大きな価値を持っているわけです。
単なる極限の公式1つだけで幾らでも楽しめるし、大きな価値を持っているわけです。
高校生の段階でそういう話を理解する必要はないと思いますが、教えている側は、自分達が教えていることが、(試験問題が解けるというようなくだらない話ではなく)普遍的な価値を持っているという立場に立てるようになることが望ましいと思います。
極限1つだけでも大きな価値を持つ。
極限1つだけでも大きな価値を持つ。
#Jupyter #Julia言語 #RStats #Ruby #Python #WolframEngine
家庭内Jupyterサーバーへのブラウザからのアクセスのスクショ
Julia v1.6.0-beta1 は非常にお勧めだが、v1.7.0-DEVは「激しい開発で相当に壊れている」のでお勧めできない。
家庭内Jupyterサーバーへのブラウザからのアクセスのスクショ
Julia v1.6.0-beta1 は非常にお勧めだが、v1.7.0-DEVは「激しい開発で相当に壊れている」のでお勧めできない。
https://twitter.com/genkuroki/status/1352828075289927680

• • •
Missing some Tweet in this thread? You can try to
force a refresh












