1/
Get a cup of coffee.
In this thread, I'll help you understand the concept of Half Life, and how it's relevant to investing.
Get a cup of coffee.
In this thread, I'll help you understand the concept of Half Life, and how it's relevant to investing.
2/
Half Life was first discovered around 1900 by the physicist Ernest Rutherford.
At the time, Rutherford was studying radioactivity in Thorium.
Half Life was first discovered around 1900 by the physicist Ernest Rutherford.
At the time, Rutherford was studying radioactivity in Thorium.

3/
Rutherford discovered that the radioactivity of a Thorium sample did not stay constant with time.
Instead, it shrank exponentially.
Every passing minute, the radioactivity got cut in half.
And after 10 minutes, it became too weak to measure.
Rutherford discovered that the radioactivity of a Thorium sample did not stay constant with time.
Instead, it shrank exponentially.
Every passing minute, the radioactivity got cut in half.
And after 10 minutes, it became too weak to measure.

4/
This observation -- made by Rutherford in ~1900 -- forms the basis for how scientists model radioactivity even today.
The model goes by the fancy name "first order kinetics".
It's based on 2 simple facts.
This observation -- made by Rutherford in ~1900 -- forms the basis for how scientists model radioactivity even today.
The model goes by the fancy name "first order kinetics".
It's based on 2 simple facts.
5/
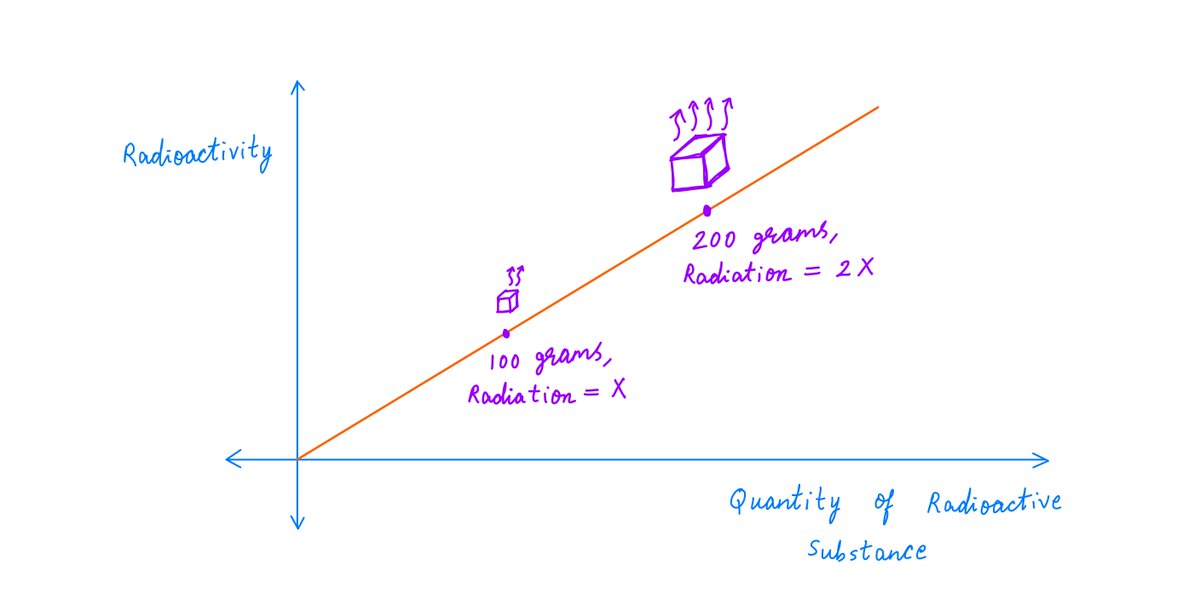
Fact 1. If we take a bigger quantity of a radioactive substance, we'll see more radioactivity from it.
For example, if you have 200 grams of Uranium, and I have only 100 grams, you'll see twice as much radiation as I do.
Seems almost obvious, no?
Fact 1. If we take a bigger quantity of a radioactive substance, we'll see more radioactivity from it.
For example, if you have 200 grams of Uranium, and I have only 100 grams, you'll see twice as much radiation as I do.
Seems almost obvious, no?
6/
But here's the thing.
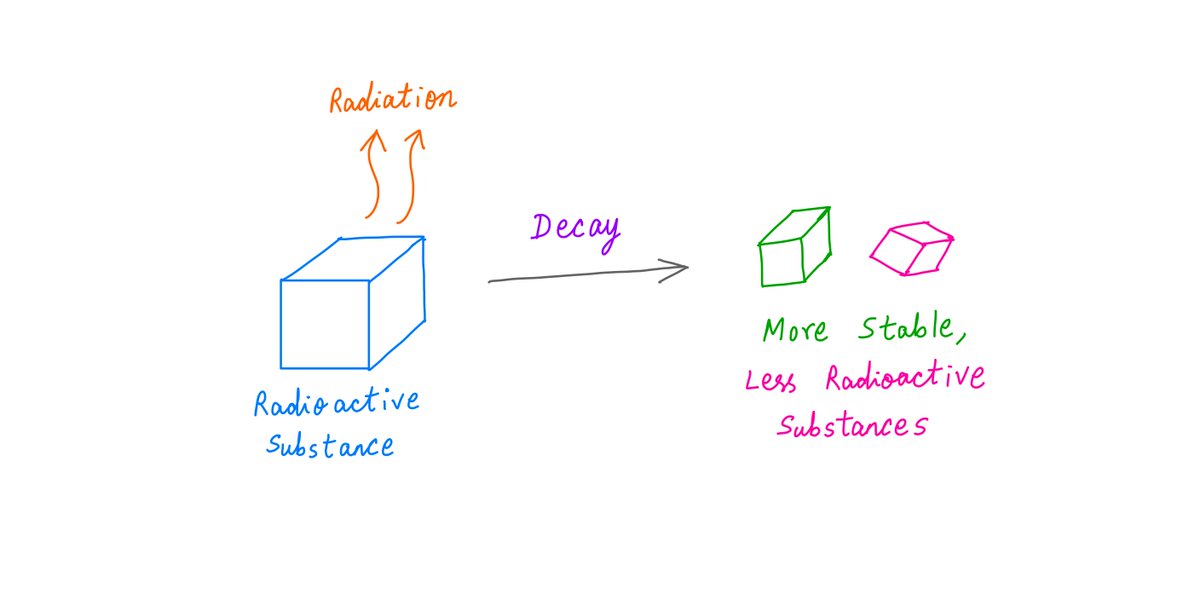
Fact 2. As a radioactive substance emits radiation, it decays into more stable (less radioactive) substances.
But here's the thing.
Fact 2. As a radioactive substance emits radiation, it decays into more stable (less radioactive) substances.
7/
So, there's a negative feedback loop here:
We may start with a large quantity of a radioactive substance. It will emit a lot of radiation.
But it will also decay fast.
And as it decays, it'll emit smaller amounts of radiation.
And its decay will also slow down over time.
So, there's a negative feedback loop here:
We may start with a large quantity of a radioactive substance. It will emit a lot of radiation.
But it will also decay fast.
And as it decays, it'll emit smaller amounts of radiation.
And its decay will also slow down over time.
8/
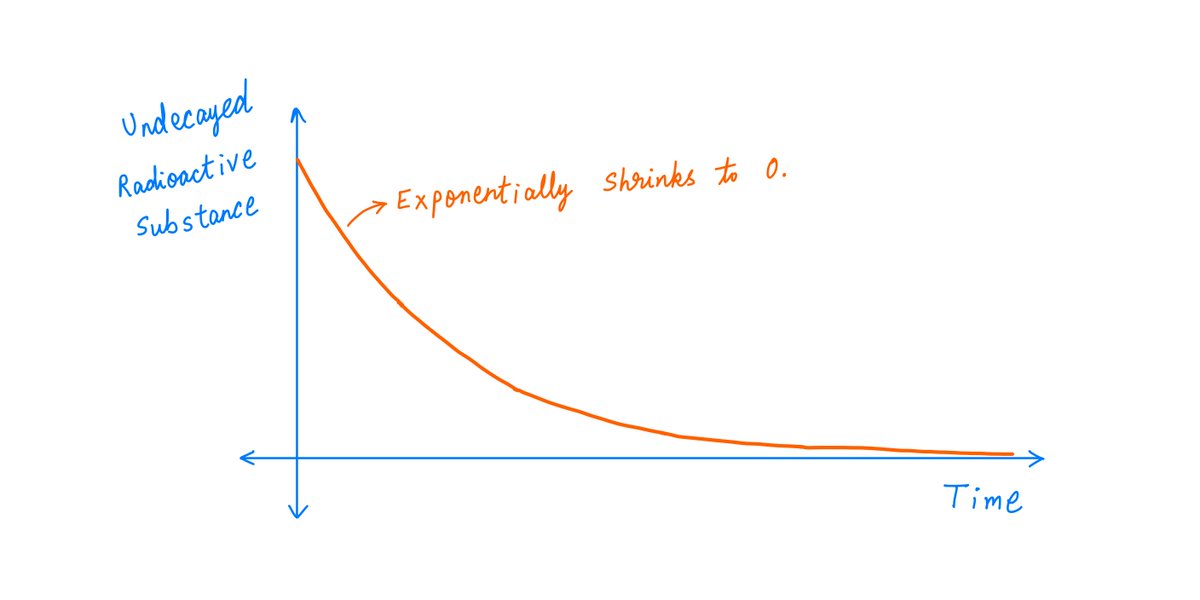
Eventually, the amount of (undecayed) radioactive substance left will approach zero.
This will happen in an *exponential* way: the rate of decay will be fast in the beginning, and will continuously keep slowing down over time.
Eventually, the amount of (undecayed) radioactive substance left will approach zero.
This will happen in an *exponential* way: the rate of decay will be fast in the beginning, and will continuously keep slowing down over time.
9/
Such exponentially decaying phenomena have a quantity called Half Life associated with them.
Simply put, it's the amount of time taken for a radioactive substance to decay so much that only half of it is left.
Such exponentially decaying phenomena have a quantity called Half Life associated with them.
Simply put, it's the amount of time taken for a radioactive substance to decay so much that only half of it is left.
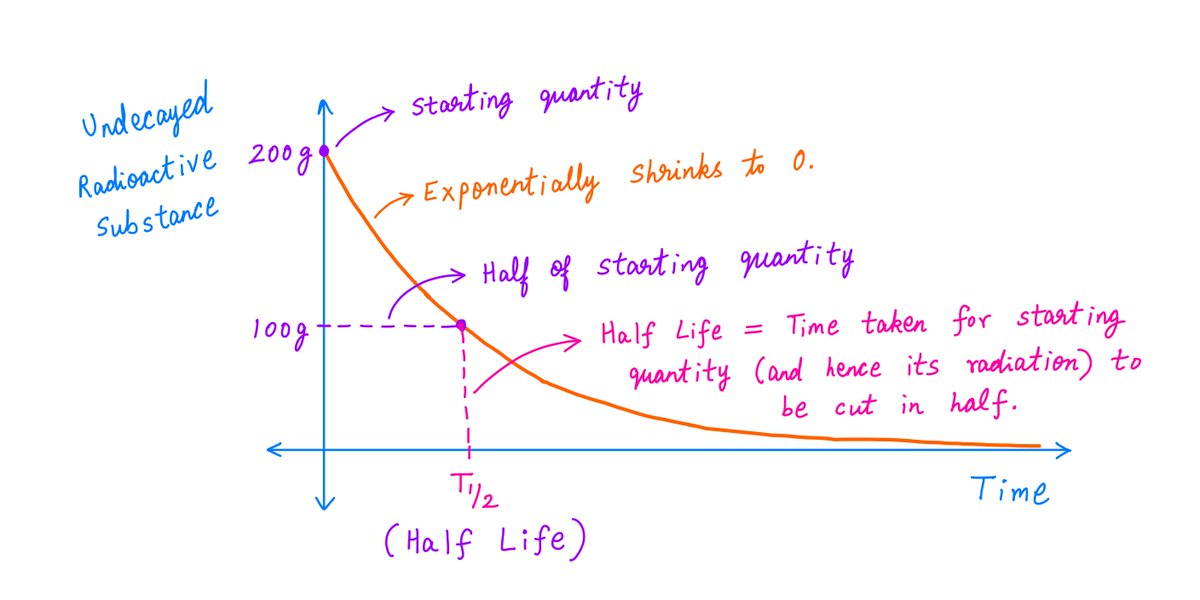
10/
For example, Rutherford observed a Half Life of 1 minute for thorium oxide.
So, if we start with 200g of this substance, only 100g will be left after 1 minute. The other 100g would have decayed.
After 2 minutes, only 50g will remain.
After 3 minutes, only 25g.
And so on.
For example, Rutherford observed a Half Life of 1 minute for thorium oxide.
So, if we start with 200g of this substance, only 100g will be left after 1 minute. The other 100g would have decayed.
After 2 minutes, only 50g will remain.
After 3 minutes, only 25g.
And so on.
11/
Note: it doesn't matter how much thorium oxide we start with.
How ever much we start with, only half of it will remain after 1 minute.
If we start with 200g, 100g will remain after 1 minute.
If we start with 400g, 200g will remain after 1 minute.
That's Half Life.
Note: it doesn't matter how much thorium oxide we start with.
How ever much we start with, only half of it will remain after 1 minute.
If we start with 200g, 100g will remain after 1 minute.
If we start with 400g, 200g will remain after 1 minute.
That's Half Life.
12/
To drive this home, here's an example from my high school physics textbook:
(I went to high school in India. The NCERT physics and math textbooks I studied from were the best! They're available for free here: ncert.nic.in/textbook.php)
To drive this home, here's an example from my high school physics textbook:
(I went to high school in India. The NCERT physics and math textbooks I studied from were the best! They're available for free here: ncert.nic.in/textbook.php)

13/
Half Life has become such a useful concept, with applications from archaeology to biology.
For example, here's an exercise problem from the same textbook -- using Half Life to do carbon dating.
See if you can solve it!
I'll give out the solution in next week's thread. 😀
Half Life has become such a useful concept, with applications from archaeology to biology.
For example, here's an exercise problem from the same textbook -- using Half Life to do carbon dating.
See if you can solve it!
I'll give out the solution in next week's thread. 😀

14/
I can hear you ask:
This is all no doubt very interesting, but how does any of it relate to investing?
You see, Half Life and inflation are closely connected.
I can hear you ask:
This is all no doubt very interesting, but how does any of it relate to investing?
You see, Half Life and inflation are closely connected.
15/
Inflation is like radioactivity.
A dollar of cash is like a radioactive substance.
As inflation hits, the purchasing power of that dollar decays exponentially with time.
Inflation is like radioactivity.
A dollar of cash is like a radioactive substance.
As inflation hits, the purchasing power of that dollar decays exponentially with time.
16/
The Rule Of 72 can be used to estimate the Half Life of a dollar:

The Rule Of 72 can be used to estimate the Half Life of a dollar:
https://twitter.com/10kdiver/status/1340366623425761280

17/
Over every Half Life, dollars held as cash will lose half their purchasing power.
For example, suppose we have a suitcase full of cash. Let's say it contains $1M.
And let's say this $1M will buy us about 100K burritos today (at ~$10 a burrito).
Over every Half Life, dollars held as cash will lose half their purchasing power.
For example, suppose we have a suitcase full of cash. Let's say it contains $1M.
And let's say this $1M will buy us about 100K burritos today (at ~$10 a burrito).
18/
Suppose inflation is 4% per year.
Then, in 18 years time, the same suitcase (with the same $1M of cash in it), will only buy us 50K burritos.
Because, between now and 18 years from now, the price of a burrito would have increased to $20.
Suppose inflation is 4% per year.
Then, in 18 years time, the same suitcase (with the same $1M of cash in it), will only buy us 50K burritos.
Because, between now and 18 years from now, the price of a burrito would have increased to $20.
19/
And in another 18 years (ie, 36 years from now), our purchasing power will be further halved.
Burritos would have again doubled in price, and our $1M then will only buy 25K burritos.
And so on. Every 18 years, our dollars will lose half their purchasing power.
And in another 18 years (ie, 36 years from now), our purchasing power will be further halved.
Burritos would have again doubled in price, and our $1M then will only buy 25K burritos.
And so on. Every 18 years, our dollars will lose half their purchasing power.
20/
In a sense, the purpose of investing our cash is to preserve (and if possible, grow) its purchasing power.
Our dollars, if kept as cash, are continuously radiating away their purchasing power at an exponential rate.
Hopefully, if invested well, they won't do so.
In a sense, the purpose of investing our cash is to preserve (and if possible, grow) its purchasing power.
Our dollars, if kept as cash, are continuously radiating away their purchasing power at an exponential rate.
Hopefully, if invested well, they won't do so.
21/
As Buffett put it in his 1980 letter:
(He used hamburgers instead of burritos, but the principle is the same!)
As Buffett put it in his 1980 letter:
(He used hamburgers instead of burritos, but the principle is the same!)

22/
The same logic holds when companies reinvest their earnings instead of paying them out as dividends.
The hope is that shareholders will see $2 in the future for every $1 they forego in dividends today.
But what counts is the *after tax purchasing power* of this $2.
The same logic holds when companies reinvest their earnings instead of paying them out as dividends.
The hope is that shareholders will see $2 in the future for every $1 they forego in dividends today.
But what counts is the *after tax purchasing power* of this $2.
23/
If the $2 comes late in the future -- after the Half Life of a dollar -- then shareholders would have been better off with the original $1.
This is why earnings growth should always be viewed relative to how much capital is required to produce it.
If the $2 comes late in the future -- after the Half Life of a dollar -- then shareholders would have been better off with the original $1.
This is why earnings growth should always be viewed relative to how much capital is required to produce it.
24/
If the *after tax* return earned by shareholders on such reinvested capital is lower than inflation, then shareholders would likely be better off if that money were never reinvested, and instead just given to them as a dividend.
For more:
If the *after tax* return earned by shareholders on such reinvested capital is lower than inflation, then shareholders would likely be better off if that money were never reinvested, and instead just given to them as a dividend.
For more:
https://twitter.com/10kdiver/status/1332742824626847744
25/
To summarize, I've found Half Life to be a useful concept when analyzing exponentially decaying things -- the purchasing power of a dollar, the share count of a company doing buybacks, etc.
And the Rule of 72 has helped me mentally calculate such things pretty easily.
To summarize, I've found Half Life to be a useful concept when analyzing exponentially decaying things -- the purchasing power of a dollar, the share count of a company doing buybacks, etc.
And the Rule of 72 has helped me mentally calculate such things pretty easily.
26/
So, I hope these ideas are useful to you as well.
Thanks for reading. Stay safe. Enjoy your weekend!
/End
So, I hope these ideas are useful to you as well.
Thanks for reading. Stay safe. Enjoy your weekend!
/End
• • •
Missing some Tweet in this thread? You can try to
force a refresh