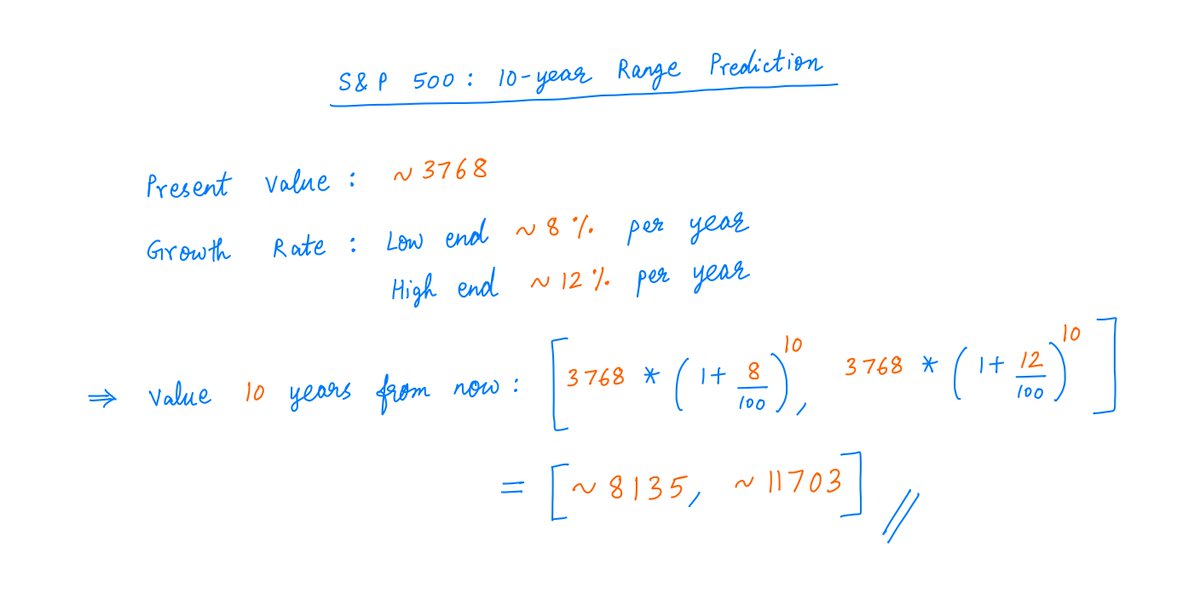Thread by @10kdiver

1/

Get a cup of coffee.

In this thread, I'll help you understand the basics of Binomial Thinking.

The future is always uncertain. There are many different ways it can unfold -- some more likely than others. Binomial thinking helps us embrace this view.

2/

The S&P 500 index is at ~3768 today.

Suppose we want to predict where it will be 10 years from now.

Historically, we know that this index has returned ~10% per year.

If we simply extrapolate this, we get an estimate of ~9773 for the index 10 years from now:

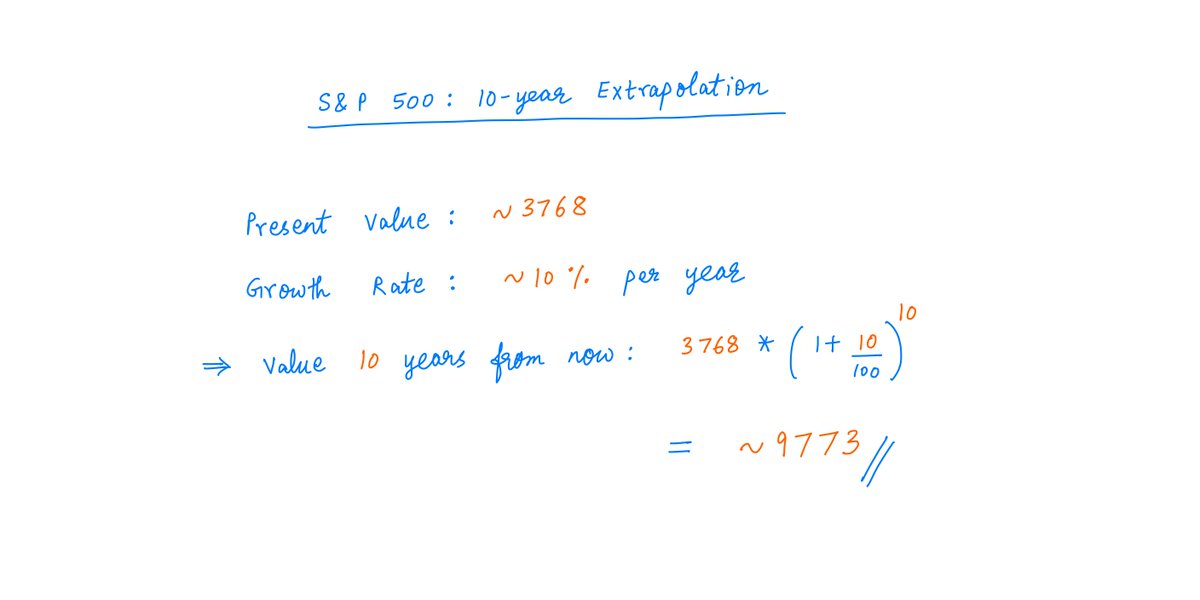
3/

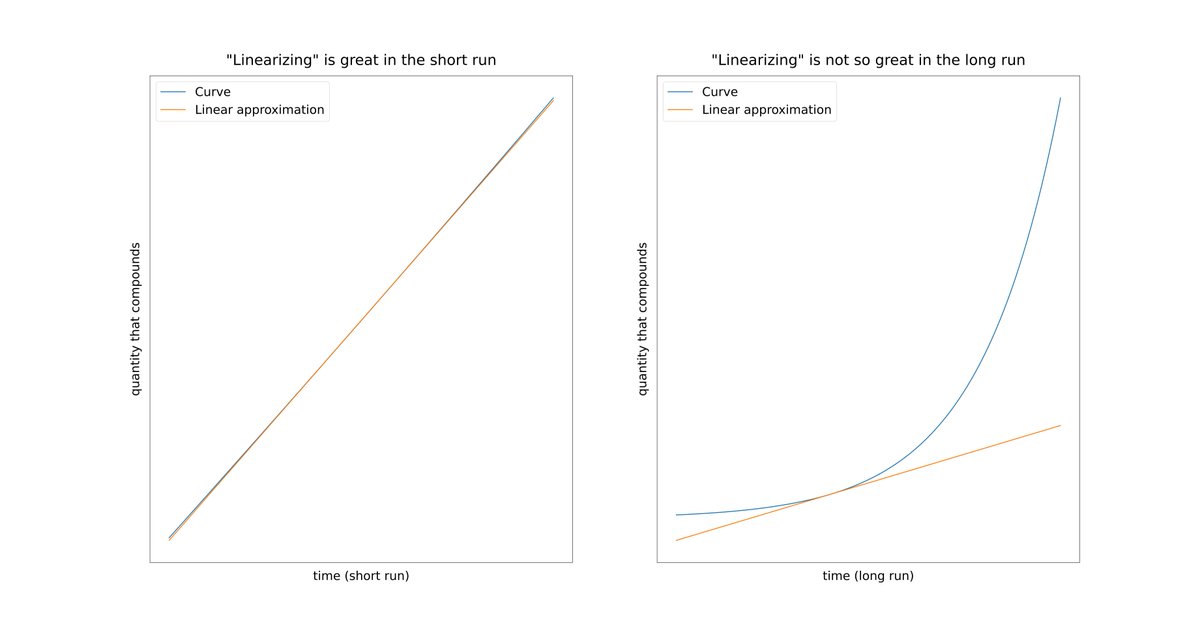
What we just did is called a "point estimate" -- a prediction about the future that's a single number (9773).

But of course, we know the future is uncertain. It's impossible to predict it so precisely.

So, there's a sense of *false precision* in point estimates like this.

4/

To emphasize the uncertainty inherent in such predictions, a better approach is to predict a *range* of values rather than a single number.

For example, we may say the index will return somewhere in the *range* of 8% to 12% (instead of a fixed 10%) per year.

5/

10 years from now, this implies an index value in the *range* [8135, 11703]:

6/

A range is more nuanced than a point estimate, but we still have a problem:

Range estimates tell us nothing about the relative likelihoods of different parts of the range.

For example, which is more likely -- the low end or high end of the range? We don't know.

7/

Ideally, we want to say something like:

10 years from now, there's a ~93% chance that the index will lie in the range [5648, 15244], and there are 60/40 odds favoring the bottom half of this range.

Binomial thinking enables us to make such *probabilistic* predictions.

8/

With binomial thinking, we can derive not just a *range* of possible outcomes, but also the *probability* of seeing each outcome in this range.

It's easiest to illustrate this with an example.

9/

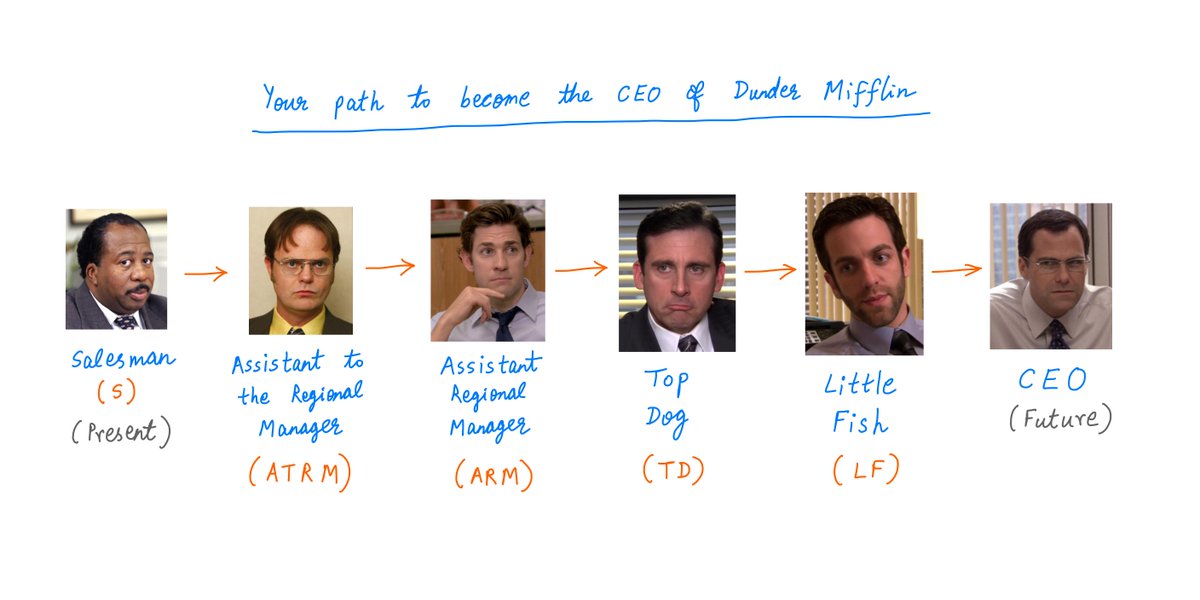
Imagine that you just joined the Dunder Mifflin Paper Company as a Salesman.

From these humble beginnings, you hope to rise quickly within the organization.

You want to become the CEO in 6 years time.

Here's your path to the top job:

10/

So, you need 5 promotions to become the CEO.

Let's say you come up for a promotion every year.

And every year, there's a 75% chance you'll get the promotion (and a 25% chance you won't).

So, what's the probability that you'll achieve your goal of becoming CEO in 6 years?

11/

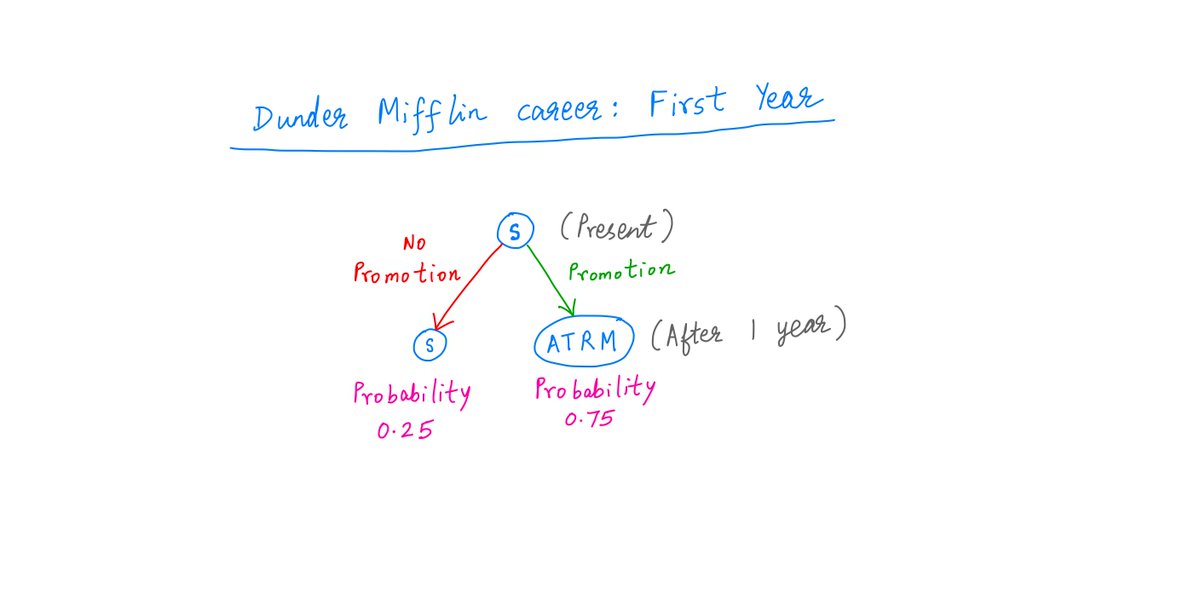
Let's tackle this one year at a time.

At the end of your first year on the job, you come up for a promotion.

If you get it, you become Assistant To the Regional Manager (ATRM). If not, you remain Salesman (S). The odds are 75/25.

12/

So, at the end of Year 1, there are 2 possible states you could be in: S (Salesman) and ATRM (Assistant To the Regional Manager).

S has a 25% probability and ATRM has a 75% probability.

13/

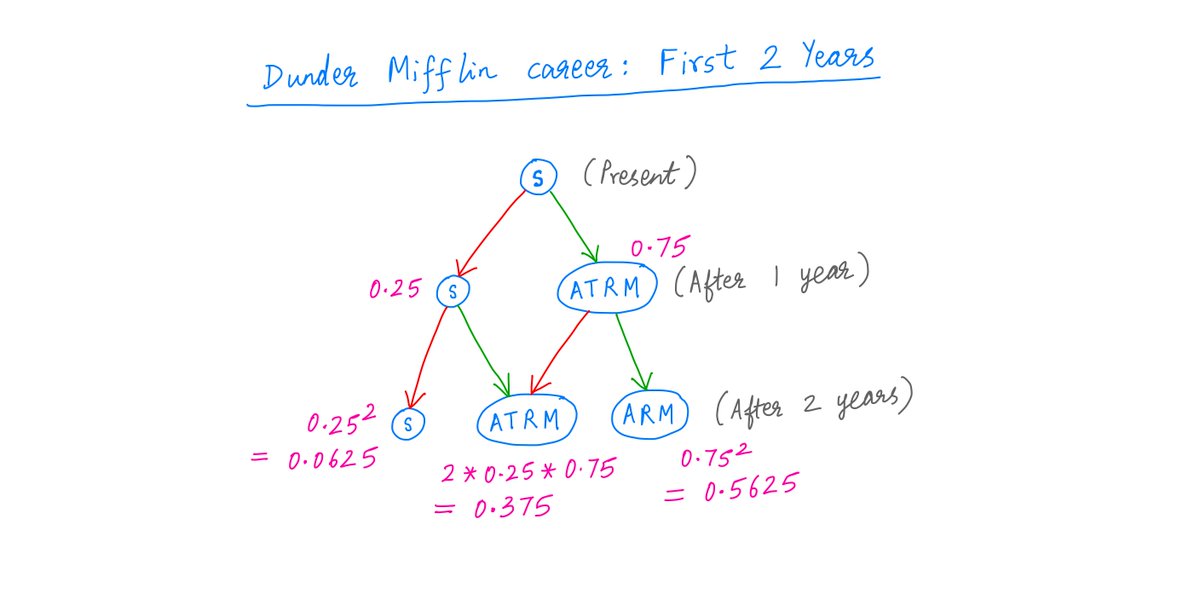
Similarly, at the end of Year 2, you again come up for a promotion.

Depending on whether you get it, there are now 3 possible states you could be in: S, ATRM, and ARM.

Again, each state has a probability (in pink below):

14/

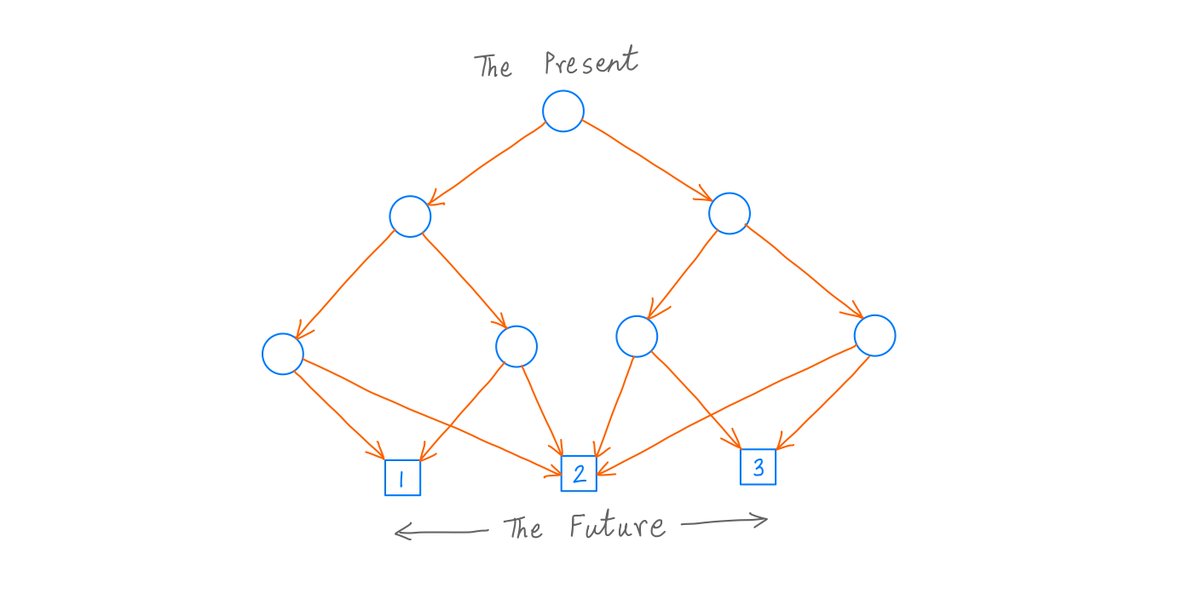
Continuing this way, we can draw up all the career trajectories you can possibly follow during your first 6 years at Dunder Mifflin.

In some of these trajectories, you achieve your goal of becoming CEO. In others, you don't.

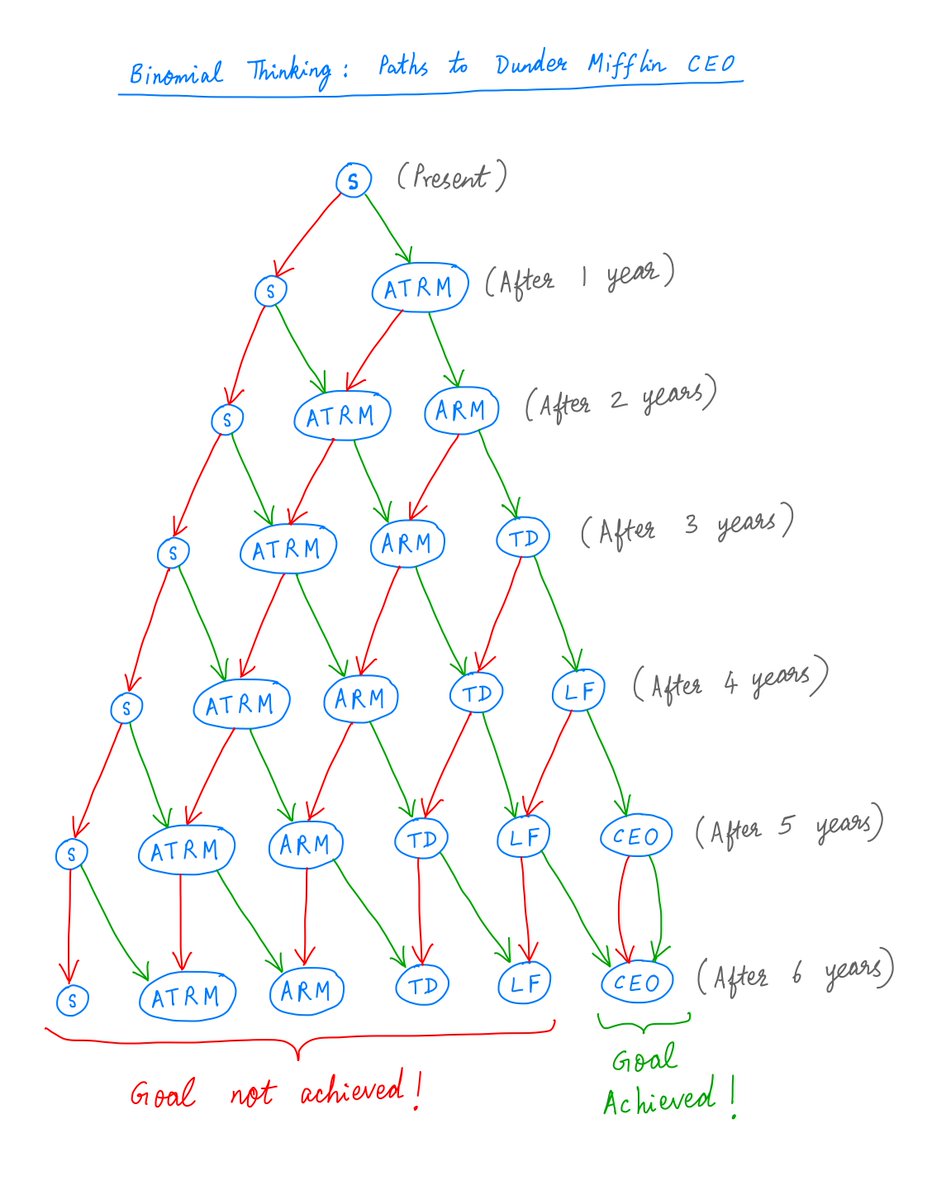
15/

And by simply propagating the 75/25 probabilities all the way down, we find that your probability of becoming CEO within 6 years is ~53.39%:

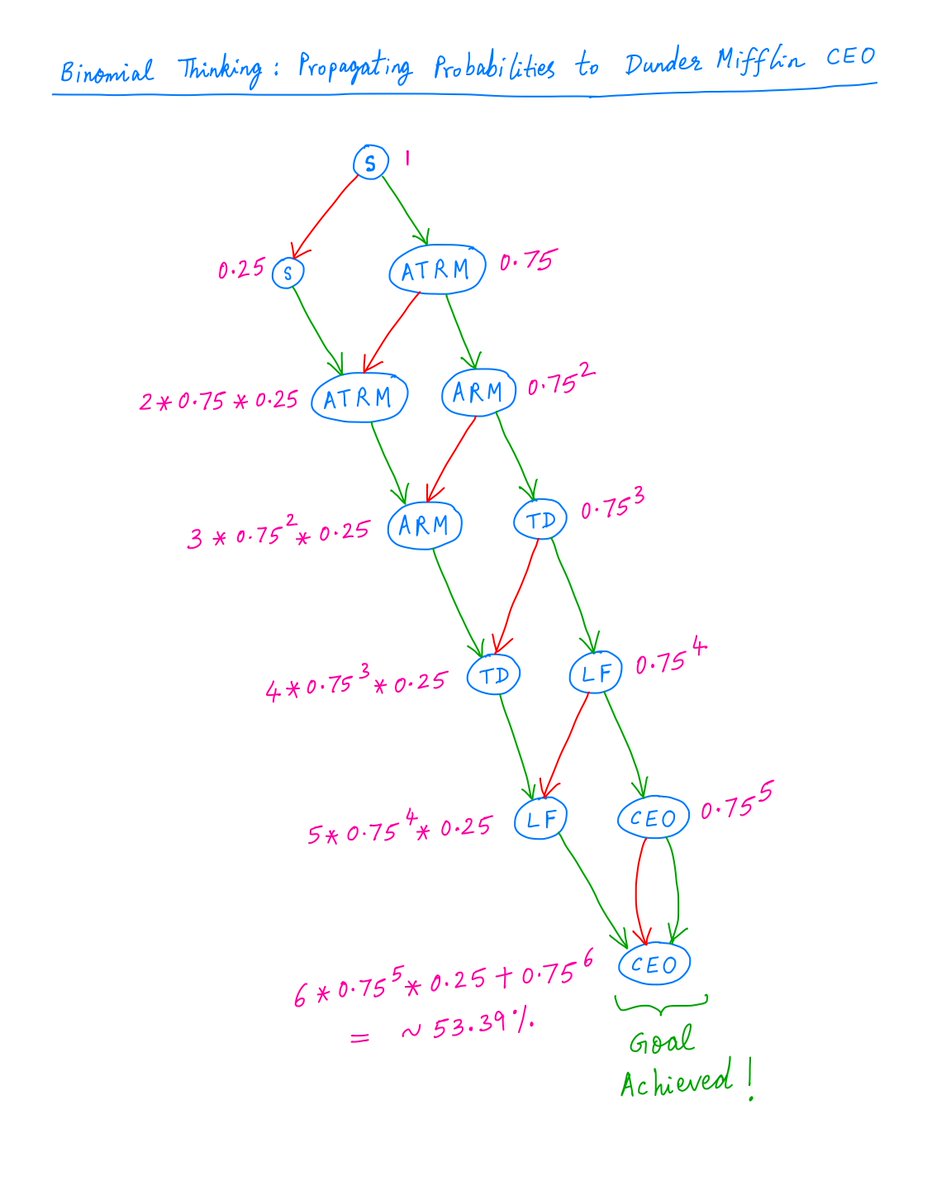
16/

This example illustrates some key features of binomial thinking.

Feature 1. Break time into small chunks.

For example, in this case, we broke your first 6 years at Dunder Mifflin into 6 1-year chunks.

17/

Feature 2. At the end of each time chunk, figure out all possible states we can be in.

For example, at the end of Year 2 at Dunder Mifflin, your possible states are: S, ATRM, and ARM.

18/

Feature 3. At each possible state, consider 2 possible scenarios and where each one leads.

The scenarios could be getting a promotion or not. The S&P 500 going up or down. An election won by a Democrat or a Republican. A guilty or not guilty court verdict. Etc.

19/

Feature 4. Account for probabilities. Propagate them top-down through the binomial diagram to work out the chances of getting various desirable and undesirable outcomes.

20/

That's pretty much all there is to binomial thinking.

As you've seen, it's a simple way to incorporate chance events and probabilistic outcomes into our analyses.

It's particularly useful when simple point estimates and range estimates prove to be inadequate.

21/

But there are also drawbacks to binomial thinking.

For example, it advocates a binary worldview. At each state, we only account for 2 possible ways the future can unfold (eg, "promotion" vs "no promotion").

22/

But often, there are more than 2 ways.

For example, the S&P 500 may go down 30%, up 5%, up 25%, etc. The possibilities are endless, but binomial logic reduces them to just 2.

Also, in many situations, the binomial diagram becomes pretty big -- and hard to analyze.

23/

But even with these drawbacks, binomial thinking is a definite step up over standard deterministic thinking.

In the land of the blind, the one-eyed man is king.

In the land of point estimators, the binomial thinker is king.

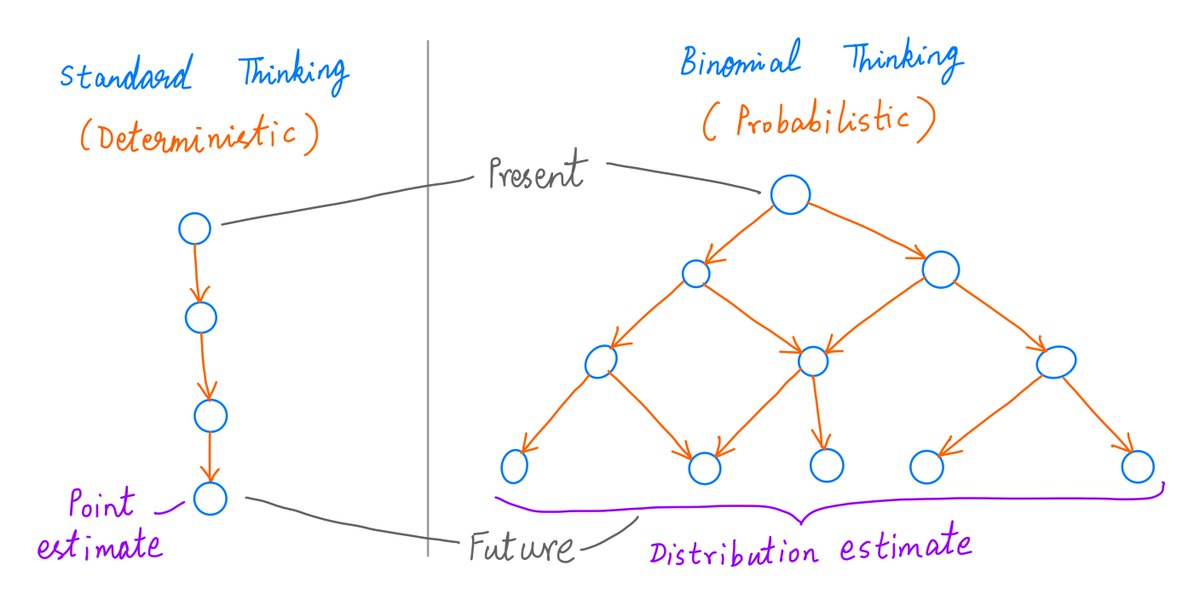
24/

Many financial calculations rely on binomial thinking. Examples include the binomial options pricing model and its cousin Black-Scholes.

Also, this paper by @mjmauboussin uses binomial thinking to value the "optionality" of businesses: capatcolumbia.com/Articles/FoFin…

25/

At every tweet of this thread, you had a binary choice: you could continue reading, or you could skip the rest of the thread.

You're that special person who elected to continue 25 times in a row. A binomial wonder.

Thank you so much!

Have a great weekend.

/End