Share this page!

黒木玄 Gen Kuroki Profile picture
Twitter logo
23 Mar, 18 tweets, 10 min read
#Julia言語

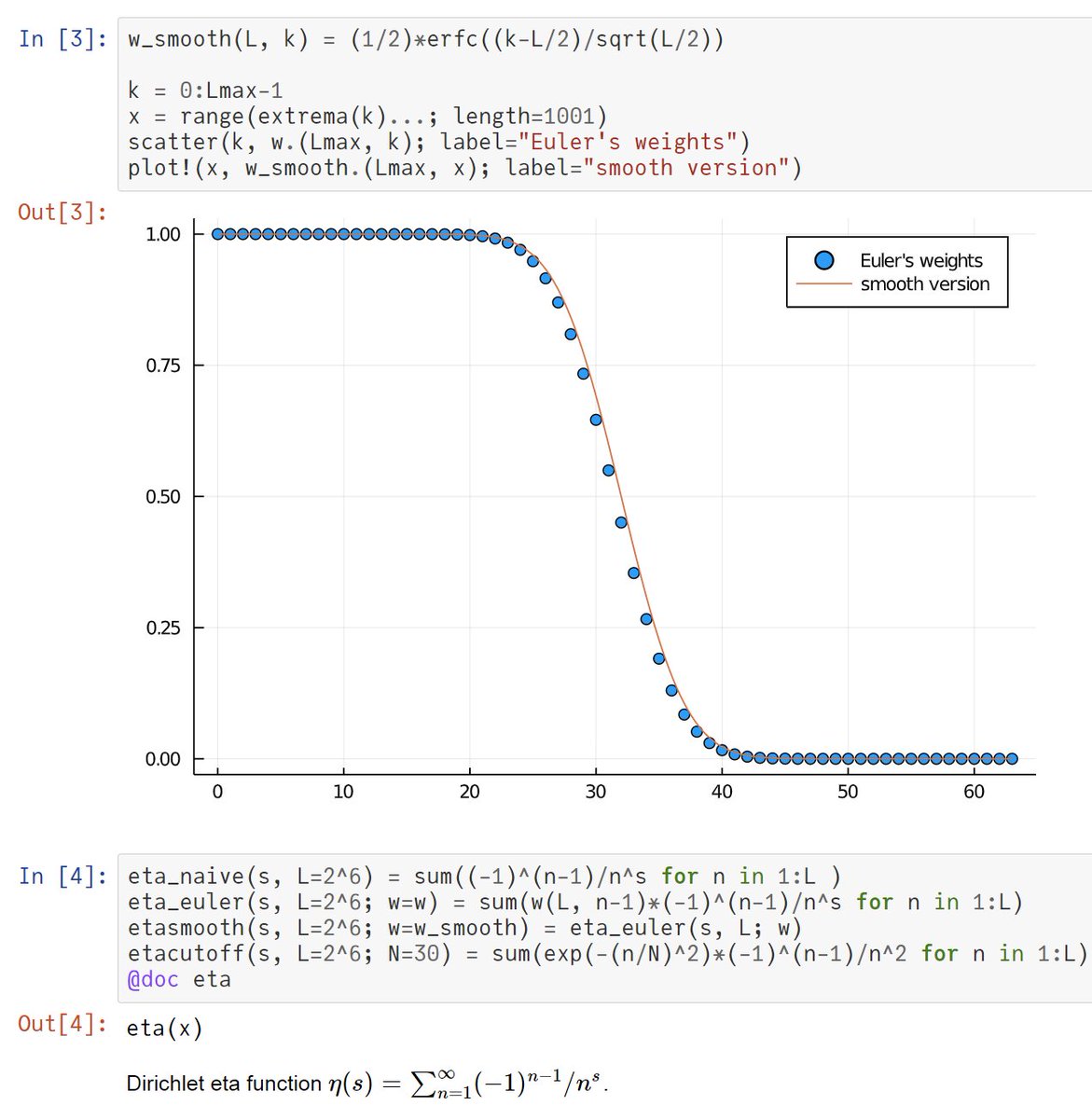
DifferentialEquations.jl のシンプルな使用例

nbviewer.jupyter.org/gist/genkuroki…
単振子

初期条件は一回転せずにすむぎりぎりの速さで揺らすこと。振子が倒立直前の状態前で行く。

この場合の運動方程式は数値的に解くのに失敗し易いので、各数値解法のテストに使えます。

添付画像→厳密解
#Julia言語

ODEProblemのデフォルトのソルバの場合

橙破線の厳密解から大幅にずれている。

正方向に倒立直前状態まで回転して、負方向に倒立直前まで行く所までは正確だが、そこから先はめちゃくちゃ。

エネルギーも全然保存されない。

これを見れば数値計算は要注意であることがよく分かる。
#Julia言語

Tsitouras' Runge-Kutta-Oliver 6 stage 5th order method で時刻の刻み幅が dt = 0.05 の場合

これは概ね正確。エネルギー保存則の側がちと不安な動き方。

DifferentialEquations.jlでは膨大な数のソルバが実装されています。
diffeq.sciml.ai/stable/solvers…
#Julia言語

ハミルトニアンで問題を与えた場合に、デフォルトのソルバを使うとこうなる。

ODEProblemのデフォルトのソルバの場合よりも、こちらの方がかなり正確です。エネルギーは保存されず、微増化傾向。
#Julia言語

ハミルトニアンで問題を与えて、Yoshida6法で dt = 0.1 の場合

dtが0.1と大きめなのに、非常にうまく数値解が求まっています。

数値解の計算法によって結果はかなり変ります。

nbviewer.jupyter.org/gist/genkuroki…
#Julia言語

みんな大好きないつものルンゲクッタ法の場合

dt = 0.1 だと粗すぎて誤差が大きいです。

この場合はexact解が楕円函数で書けることを知っているので、誤差が大きいことが分かりますが、そうでない場合は闇の中になる場合がある。

エネルギーは微減傾向。
#Julia言語 時間の刻み幅が一定の古典的なルンゲクッタ法はDifferentialEquations.jlには実装されていません。SimpleDiffEq.jlが別に必要。

さらに本当にみんな大好きなアレになっていることを確認するために自分でもルンゲクッタ法のコードを書いて一致することも確認しています。
#Julia言語 古典的な時間の刻み幅が一定のルンゲクッタ法は Julia の DifferentialEquations.jl の世界では「普通は使わない方法」扱いになっている感じです。

時代が進んで数学的技術が発展するとこういうことになるので、知識を時代に合わせてアップデートして行く必要がある。
#Julia言語 DifferentialEquations.jl には膨大な量の上微分方程式の数値解法が実装されています。

そのうちの一部を使った場合

このツイートの添付画像に載せた方法はほぼことごとく失敗している。😱😊🤣😭😆
#Julia言語 シンプレクティック法

dt はわざと大きめの値の 0.1 にしてあります。

McAte5(dt=0.1)では振子が倒立状態を超えてあっちに行ってしまっている(笑)

こういうのは失敗している場合がないと面白くない。

他にもシンプレクティック法が沢山実装されています↓
diffeq.sciml.ai/stable/solvers…
#Julia言語

nbviewer.jupyter.org/gist/genkuroki…
倒立直前まで振れる単振り子

↑これを見れば、JuliaのDifferentialEquations.jlで微分方程式の問題を与えて解く基本的な方法が分かります。

ハミルトニアンを与えて解かせる方法も分かる！
自動微分で正準方程式を正確に計算しているはず。
#Julia言語 DifferentialEquations.jl はNASAで使われている。

従来の方法が15000倍高速化されたらしい(笑)
#Julia言語

discourse.julialang.org/t/julia-and-th…
【今では、Juliaはブラジルの宇宙計画の一部】

やはりDifferentialEquations.jlを使っているらしい。
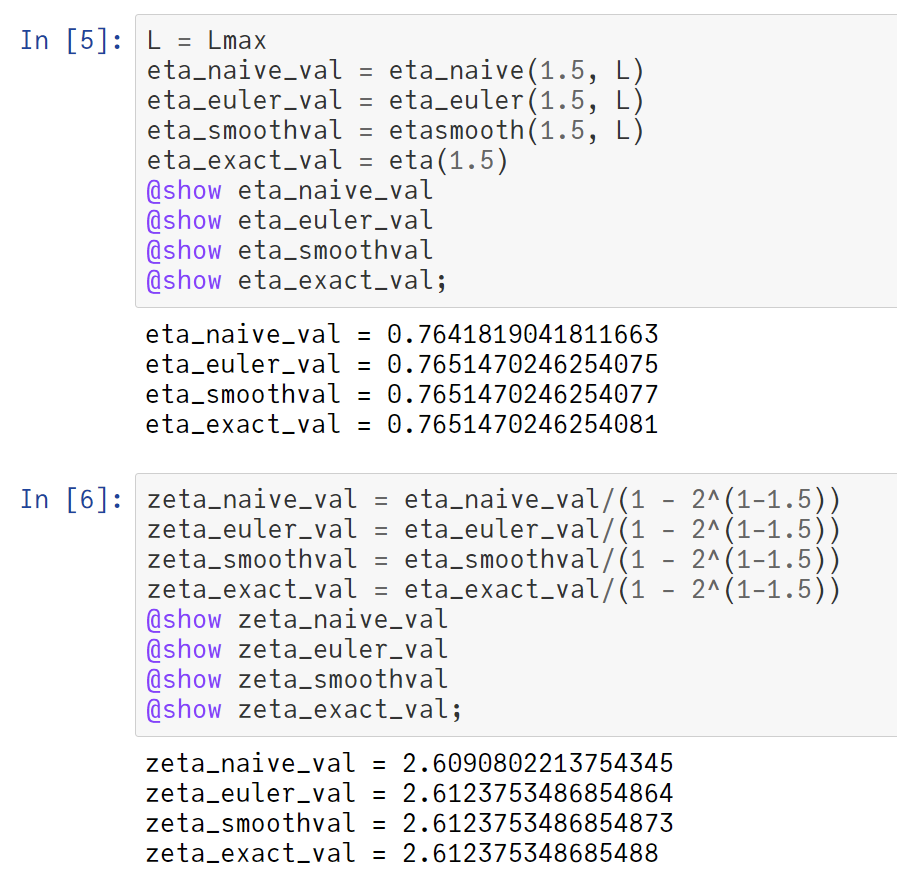
#Julia言語 おまけ。既出の

nbviewer.jupyter.org/gist/genkuroki…

では、PhysicalConstants.jlから

g = 9.80665 m s^-2

を取得して使っています。振子の長さは1mです。Unitful.jlを使って、l = 1.0m と定義している。

DifferentialEquations.jlでは単位付きの数量を直接扱えるのですが、計算は遅くなる。
#Julia言語 私も Yoshida6 をいつも使っている。

他にも色々試してみて「Yoshida6、わるくねえ❤️」という感じ。
#Julia言語 みんな大好きらしい Yoshida6 をDifferentialEquations.jl で使う3つの方法が、既出の

nbviewer.jupyter.org/gist/genkuroki…

にあります。

SecondOrderODEProblem
DynamicalODEProblem
HamiltonianProblem

の3つの問題で、数値計算がうまく行く例を作るためにYoshida6を使っています。
#Julia言語 ハミルトニアンを与える方法だと、ハミルトニアンから正準方程式を作るところで無駄に誤差が発生することを恐れるかもしれませんが、DifferentialEquations.jlでは自動微分で正準方程式を正確に計算しています。

ハミルトン函数をJulia語で書いて初期値を与えるだけでいいのは楽ちんです。
#Julia言語 ただし、「幅を持った数値」で微分方程式の数値階を求めたい場合には、ForwardDiff.jlとの相性の都合でHamiltonianProblemが使えなくなる場合があります。

その場合には正準方程式を計算して、SecondOrderODEProblemまたはDynamicalODEProblemを使えば大丈夫です。

• • •

Missing some Tweet in this thread? You can try to force a refresh
　

Keep Current with 黒木玄 Gen Kuroki

黒木玄 Gen Kuroki Profile picture

Stay in touch and get notified when new unrolls are available from this author!

Read all threads

This Thread may be Removed Anytime!

PDF

Twitter may remove this content at anytime! Save it as PDF for later use!

Try unrolling a thread yourself!

how to unroll video
  1. Follow @ThreadReaderApp to mention us!

  2. From a Twitter thread mention us with a keyword "unroll"
@threadreaderapp unroll

Practice here first or read more on our help page!

More from @genkuroki

黒木玄 Gen Kuroki Profile picture
25 Mar
#数楽

多項式f∈ℝ[x]に「a∈ℝをf(a)∈ℝを対応させる函数」を対応させる写像は単射なので、多項式fとそれに対応する実数の函数を区別しなくも大丈夫。(無限体でもOK)

有限体F上の多項式g∈F[x]に「a∈Fをg(a)∈Fを対応させる函数」を対応させる写像は単射でないので、それらを同一視できない。
#数楽 例えば二元体𝔽₂={0,1} (1+1=0)について、𝔽₂上の多項式としてxとx²は異なるが、𝔽₂上の函数としてはどちらも恒等写像になって等しくなってしまう。

xとx²を𝔽₂の2次拡大𝔽₄=𝔽₂[α] (α²=α+1)上の函数とみなしたものは互いに異なる。

こういう具体例がノータイムで出て来ることが大事。
#数楽 面倒なのは有理函数(多項式環の分数体の要素)に対応する「函数」の場合。

有理函数ごとに定義域も変わるので、異なる定義域を持つ函数達を同時に扱うための「処理」が必要になる。(これには複数の処方箋がある。)

結果的に、無限体の場合には、有理函数と対応する「函数」は同一視可能になる。
Read 7 tweets
黒木玄 Gen Kuroki Profile picture
25 Mar
大学生相手であっても、必要な数学の実力は結構高いので、統計学を教えるのに苦労しています。

高校生相手に検定が「お墨付きが得られる道具」であるかのように教えられてしまうようになったら最悪。

あと、信頼区間がモデル依存であることも(大学生と同様に)教えることにならないと思う。
現実には世界的にかなり悲惨なことになっていて、論文を日常的に書いている研究者であっても、統計的検定を「お墨付きが得られる道具」扱いしている人達が沢山いるんじゃないか？

そういう現状は若くて優れた研究者が育つことを妨害していると思う。

こういう問題を維持固定しないような教育が必要。
まだ高校生なのに、「統計的に有意である！」を水戸黄門的な「ひかえおろう！」と同じ意味で使うようになったら最悪(笑)
Read 24 tweets
黒木玄 Gen Kuroki Profile picture
25 Mar
#Julia言語 リポジトリの方の公式マニュアルに以下が追加されましたね。

* 引数の型の過剰な制限はよくある間違いです。疑わしいなら引数の型を書くのをやめましょう。

* Juliaでは戻り値の型宣言はほとんど使われません。一般に「型安定」な函数を書くべきです。

github.com/JuliaLang/juli… Image
#Julia言語 具体的には

fib(n::Int) = n ≤ 2 ? one(n) : fib(n-1) + fib(n-2)

はよくある間違で、

fib(n)::Int = n ≤ 2 ? one(n) : fib(n-1) + fib(n-2)

も誤りです。どちらでもBigIntによる計算が不可能になる。よく分からないなら

fib(n) = n ≤ 2 ? one(n) : fib(n-1) + fib(n-2)

でよい。
#Julia言語 無用に引数の型を制限してしまううようだと、NASAでは仕事をできなくなります。(NASAでもJuliaを使っている)
Read 11 tweets
黒木玄 Gen Kuroki Profile picture
24 Mar
#Julia言語 (1-2^(1-s))ζ(s) は交代級数になりEuler変換が使える。Euler変換を使えば数十項でFloat64の精度を使い切った計算が可能。

①オイラー変換のウェイトのグラフ
②64項の和の計算結果
③正確な値との相対誤差の常用対数、横軸Lは項数

Euler変換はかなり強力。

nbviewer.jupyter.org/gist/genkuroki… ImageImageImage
#Julia言語 Euler変換とは、1つ前のツイートの1つ目の添付画像で示された謎のウェイト w^{(L)}_k をかけて (-1)^k a_k を k=0からL-1まで足し上げると、(-1)^k a_k のk=0から∞までの和の良い近似になるという魔法のような話。

1つ前のツイートのLは2^6=64.
#Julia言語 #数楽 (1-2^(1-s))ζ(s) のEuler変換は複素平面全体で収束するので、ζ(s)の近似計算にも使える。

効率はそんなに良くないが、リーマン予想の数値的確認や視覚化をそれで行うこともできる。

非自明な零点の周囲のプロットもオイラー変換を知っていれば容易に可能である。
Read 4 tweets
黒木玄 Gen Kuroki Profile picture
24 Mar
#Julia言語 もう何度目になるか分かりませんが、私もdual numbersを実装してみた。

添付画像2の @ code_warntype と @ btime の結果に注目。この2つの確認は必ずやった方がよい。続く

ソースコード↓
nbviewer.jupyter.org/gist/genkuroki… ImageImageImageImage
#Julia言語 自動微分の仕組みのdual numberパートは易しい部分。

難しいのは大量の函数を合成してできる函数の微分をどのように効率的に求めるか。

行列A,B,C,Dのサイズによって、A(B(CD))と((AB)C)Dで計算にかかる時間が大きく違う場合がある(そのことは行列の積の定義さえ知っていれば理解可能)。
#Julia言語 Juliaで積極的に計算を遅くするには、

① グローバル変数の値を引数を経由せずに函数の中で中で使う。

② structを

struct Foo
a
b
end

のように定義して使う。もしくはこれのバリエーション。

あとほとんどの場合に mutable struct は必要ない。
Read 8 tweets
黒木玄 Gen Kuroki Profile picture
24 Mar
悪ふざけ論文のネタ：

* f(a,b,c,…)の中の個人aを特別扱いして、a.f(b,c,…) のように書き、函数fをaの所有物とするアイデアは極めて資本主義的。

* それに対抗する解放運動として多重ディスパッチが提案されて来たが、ことごとく資本主義に敗北して来た。

* 解放運動にとってJuliaは(略)
上のツイートはネタ(冗談)なので要注意。
axiom of equality を「平等の公理」だと誤解させて(本当は「等号の公理」)、さらに axiom of choice を「(産むか産まないかの)選択(を認める)公理」と読ませることに成功したパロディ論文は有名。
physics.nyu.edu/faculty/sokal/…

他にも滅茶苦茶で笑えるのですが、アクセプトされて大騒ぎになった。
Read 4 tweets

Did Thread Reader help you today?

Support us! We are indie developers!

This site is made by just two indie developers on a laptop doing marketing, support and development! Read more about the story.

Become a Premium Member ($3/month or $30/year) and get exclusive features!

Become Premium

Too expensive? Make a small donation by buying us coffee ($5) or help with server cost ($10)

Donate via Paypal Become our Patreon

Thank you for your support!

Follow Us on Twitter!

Like this author's thread?

Get emails when @genkuroki has new unrolls!

Check out other threads from @genkuroki!

Read all threads by @genkuroki