Thread by @ObjectifDataSci

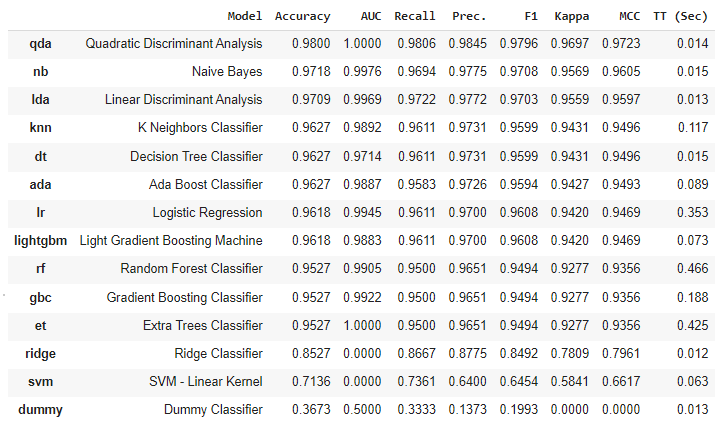
1. Aujourd'hui on va revoir nos grands classiques en #MachineLearning dans le domaine du #NLP

Nous allons revoir dans le détail comment transformer des mots en vecteurs, grâce à l'algorithme #word2vec #skipGram

Ready?

🔽🔽 Thread

2. Commençons ce thread par une évidence, mais qu'il convient de rappeler

Les algorithmes de Machine Learning ne savent pas traiter directement des mots et des lettres

Donc dès que l'on veut faire du #NLP, il faut trouver un moyen de transformer les mots en nombres

3. Une des premières intuitions que l'on peut avoir, c'est de prendre l'ensemble des mots avec lesquels on veut travailler, et de leur donner à chacun un indice, en construisant un dictionnaire

Dans ce cas, chaque mot pourra être représenté par un nombre unique (son indice)

4. On peut même s'aider de cette indexation pour construire ce qu'on appelle un vecteur "One Hot Encoding"

Chaque mot sera représenté par un vecteur de dimension égale au nombre de mots, et n'aura que des zéros sauf à l'indice où se trouve le mot dans le dictionnaire

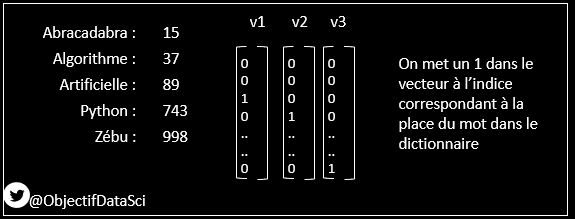
5. Cette façon de faire est par contre très limitée et peu efficace : en effet les vecteurs ne renferment pas beaucoup d'information utile (que des zéros, sauf à un indice)

Seule la "position" dans le dictionnaire est donnée par cette représentation

> sparse representation

6. Les chercheurs ont alors eu l'idée d'utiliser un grand principe donné par JR Firth en 1957, qui était un linguiste anglais vivant au 20ème siècle

Selon lui, le sens d'un mot dépend directement des autres mots qui se trouvent souvent près de lui

7. C'est l'idée de la Distribution Sémantique

ou Distributional Semantics en anglais

en.wikipedia.org/wiki/Distribut…

8. Si on suit ce principe, deux mots qui sont FREQUEMMENT PROCHES doivent renfermer le MEME SENS

A contrario, les mots que l'on voit jamais ensemble doivent avoir des sens très éloignés.

9. Le modèle #word2vec va donc construire pour chacun des mots une représentation vectorielle, de sorte que la probabilité de trouver les mots qui sont souvent dans le même contexte soit maximisée

Pas de panique si vous ne comprenez pas tout, on va y aller pas à pas

10. Imaginons que l'on représente chaque mot par un vecteur de dimensions 100

Et imaginons que l'on travaille avec un vocabulaire ne comportant que 1000 mots (c'est limité, mais c'est exprès pour l'exemple)

11. Pour mesurer la probabilité que des mots soient voisins, on va calculer le PRODUIT VECTORIEL des deux vecteurs

Ce calcul donnera un nombre qui sera d'autant plus élevé que les vecteurs sont proches

12. On prend ensuite l'exponentielle de ce produit vectoriel

Ce nombre sera toujours positif grâce à l'exponentiel, est d'autant plus grand que le produit vectoriel est grand

13. Et comme on veut une probabilité à la fin, on divise chacune des exponentielles par la somme des exponentielles

Cela donnera bien une probabilité (leur somme vaudra 1)

14. Dans notre exemple à 1000 mots, si on veut calculer la probabilité d'avoir le mot "guitare" lorsqu'on a le mot "concert" ...

15. On prend les 1000 mots et on fait le produit vectoriel avec les 1000 mots (dont lui même)

On obtiendra donc 1000 indices de vraisemblance, qu'on passe ensuite à l'exponentielle, et qu'on divise ensuite par la somme des exponentielles

La somme des probabilités vaudra alors 1

16. On reprend un peu le principe de la fonction #Softmax, utilisée massivement dans les modèles de classification

17. Ce que va faire l'algorithme skip gram, c'est qu'il va apprendre les composantes de chacun de ces vecteurs

Et ces vecteurs donneront les probabilités que les mots soient voisins, tels qu'on les trouve dans les textes qui vont servir au training

18. Une chose à bien comprendre dans l'algorithme skip-gram c'est la notion de fenêtre

C'est un paramètre qui définit le voisinage

Deux mots sont voisins s'ils se trouvent à moins de n mots, n étant égal à la fenêtre

19. L'algorithme va donc prendre tous les textes donnés dans la phase d'apprentissage

Ensuite, il va prendre chacun des mots du texte (mot central) et regarder quels sont les mots dans son contexte (le paramètre fenêtre) - le mot contexte

20. Et il va faire converger via une descente de gradient chacune des composantes des vecteurs

de sorte que les probabilités (produit vectoriel, exponentiel et normaisation) représentent bien la distribution rencontrée dans les textes (mot central et contexte)

21. La magie de l'histoire est que quand on optimise tout cela, les composantes de chacun des vecteurs s'alignent

A la fin, les mots que l'on voit souvent dans le même contexte, auront des vecteurs proches et similaires

22. C'est grâce à cela qu'on peut faire ensuite des opérations comme

Roi - homme + femme = Reine

ou France - Paris + Espagne = Madrid

Tout cela en regardant simplement le contexte de chacun des mots

23. Ce type d'algorithme a permis de nombreuses avancées pour le #NLP

Avant l'arrivée des transformers dont j'ai déjà parlé