Thread by @ObjectifDataSci

1. Hello

les réseaux #RNN de type #LSTM et #GRU sont des réseaux qui sont généralement mal compris

Je vais essayer dans ce thread de les expliquer clairement

on va commencer par voir dans le détail les GRU (Gated Recurrent Unit).

Ready?

🔽🔽

#datascience #machinelearning

2. Le principe d'un réseau récurrent RNN est relativement simple

Il s'applique à des données de type séquence c'est à dire des données qui se suivent dans le temps et dont l'ordre est important (Time Series, Speech, texte, musique, ....)

3. Dans leur forme simple, les RNN sont des réseaux de neurones classiques

avec comme différence le fait que la sortie du réseau au temps t soit mis en entrée au temps t+1

Cela permet de conserver une mémoire de ce qui a été calculé au préalable par le réseau

4. Ainsi la réponse du réseau au temps t+1 dépendra

> de la nouvelle entrée dans le réseau au temps t+1

> mais également de toutes les sorties passées que le réseau a déjà fourni

5. L'idée est belle

mais pratiquement les RNN ne fonctionnent pas très bien

Ils atteignent rapidement des limites, car ils ont du mal à conserver une mémoire longue

à cause principalement de problème au niveau du l'apprentissage (Gradient Vanishing)

6. Il y a eu des propositions d'améliorations assez astucieuses pour ces réseaux récurrents

des réseaux #LSTM (Long Short Term Memory) et #GRU (Gated Recurrent Unit)

Les GRU sont une version simplifiée des LSTM, et c'est ce qu'ont va voir dans ce thread

7. L'idée globale de ces réseaux est de créer des portes (gates en anglais)

et ces portes vont apprendre ce qu'on doit retenir du passé

Cela permet une meilleure rétention de la mémoire au fil de l'apprentissage

8. Et la façon de filtrer ce que l'on garde ou pas est APPRIS par le réseau

Pendant l'apprentissage, le réseau va apprendre ce qu'il faut garder au fil du temps

Cela permettra de garder une information beaucoup plus longtemps dans la séquence, si celle-ci est importante

9. Commençons par un schéma d'un RNN classique

La sortie a(t) (a pour ACTIVATION) dépend directement de la sortie a(t-1) et de l'entrée x(t)

Cette dépendance est représentée par la matrice Wa qui a été apprise

Une fonction d'activation est appliquée (tanh)

10. Petite précision sur la notation concernant la matrice Wa

En fait, il y a deux matrices Wa (Waa et Wat) qui s'appliquent respectivement sur a(t-1) et x(t)

Mais en concaténant les matrices, et les vecteurs on peut simplifier l'écriture

Ce que l'on choisit de faire

11. Ce que le GRU (version simplifiée) apporte, c'est la matrice Gu (G : Gate et u : Update)

Cette matrice de coefficients entre 0 et 1 retire une partie de la réponse classique du RNN (a(t)) et la remplace par une partie de a(t-1)

Cela permet de mieux conserver la mémoire

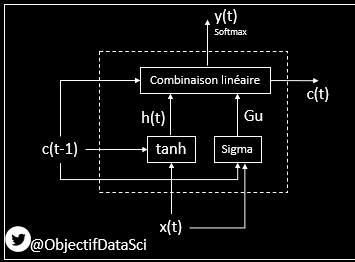
12. schéma du GRU simplifiée

Comme pour le RNN, on a l'activation en fonction de de l'entrée X(t) et de la sortie du réseau en (t-1)

appelé c(t-1), c pour Memory Cell

Appelons maintenant h (h pour hidden) cet équivalent de la sortie vue pour les RNN Vanilla

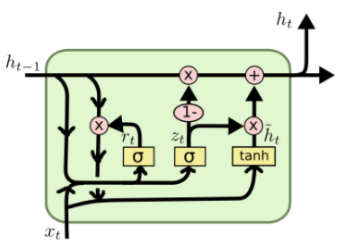
13. En plus de h(t), on calcule aussi cette matrice Gu faite de nombres entre 0 et 1 (pourcentages)

et qui représentent les pourcentages que l'on garde de h(t)

Pour cela on fait appel à l'opération matricielle de Hadamard

fr.wikipedia.org/wiki/Produit_m…

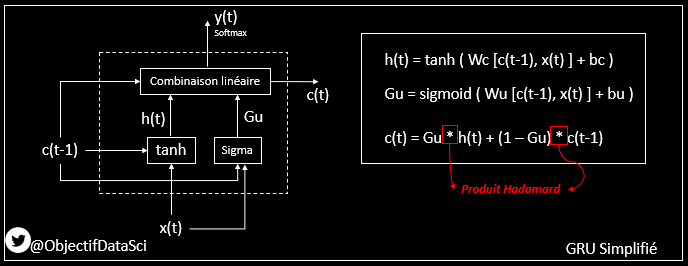
14. Cette opération matricielle, c'est simplement une multiplication de terme à terme

qui dans ce cas donnera en résultat ce que l'on garde de h(t), en fonction des coefficients de Gu (qui varient entre 0 et 1, et qui sont donc des pourcentages)

15. Et ce que l'on a pas gardé (la proportion pour compléter Gu)

on le remplace par C(t-1)

en respectant les proportions au final (c'est à dire en faisant 1-Gu)

16. Cette matrice d'oubli ou de remplacement Gu

elle est apprise également en utilisant les entrées X(t) et les sorties historiques C(t-1)

C'est la fonction logistique qui est utilisée comme fonction d'activation pour avoir un pourcentage (pourcentage d'oubli)

17. En synthèse pour le GRU simplifié

> on calcule h(t) qui est l'équivalent de la sortie classique d'un RNN basique, en fonction de c(t-1) et x(t)

> on calcule la matrice Gu en fonction de c(t-1) et x(t)

18.

> et on calcule c(t) grace à Gu

Pour le calcul de c(t), Gu détermine le pourcentage de ce que l'on garde de h(t) et ce qu'on rajoute de c(t-1) pour le calcul de c(t)

19. Dans la version complète de la GRU

lors du calcul de h(t), on va aussi appliquer des coefficients à c(t-1) pour n'en prendre qu'une partie, celle qui est pertinente

On va utiliser pour cela une nouvelle gate qu'on va appeler Gr, r pour "relevant" ou "reset"

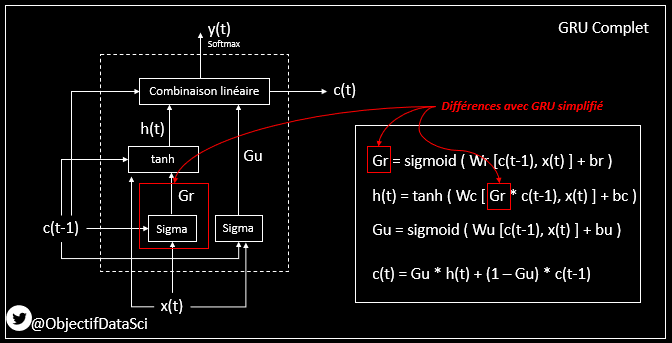
20. Ensuite, comme pour la version GRU simplifiée, la sortie au final dépendra de cette sortie classique (amputée par la matrice Gu) et d'un petit peu d'historique qu'on rajoute via 1-Gu

21. On remarquera que les deux Gates Gu et Gr ont comme fonctions d'activation la fonction logistique -> cela donne bien des pourcentages

Et toutes les deux sont apprises en prenant comme paramètres les nouvelles entrées et l'historique, en construisant les matrices Wu et Wr

22. En synthèse

> dans un réseau RNN classique

la sortie c(t) (ou a(t)) dépend directement de

- x(t) (les données d'entrée)
- et de c(t-1) (la sortie t-1)

23.

> dans un réseau GRU simplifié

la matrice Gu est apprise (via c(t-1) et de x(t)).

Gu permet de ne garder qu'une partie de h(t) (qui est fonction de c(t-1) et x(t))

et de compléter par c(t-1)

Cela permet d'être meilleur dans la conservation de la mémoire du réseau

24. Et dans un réseau GRU Complet

> c'est comme pour la version GRU simplifiée

> sauf que dans le calcul de h(t), on ne prend qu'une partie de c(t-1) grâce à une matrice Gr qui est apprise en fonction de c(t-1) et x(t)

25. J'espère que c'est plus clair pour vous maintenant pour les GRU

Si vous avez saisi ces explications, vous comprendrez facilement le fonctionnement des LSTM que je vais vous montrer tout prochainement