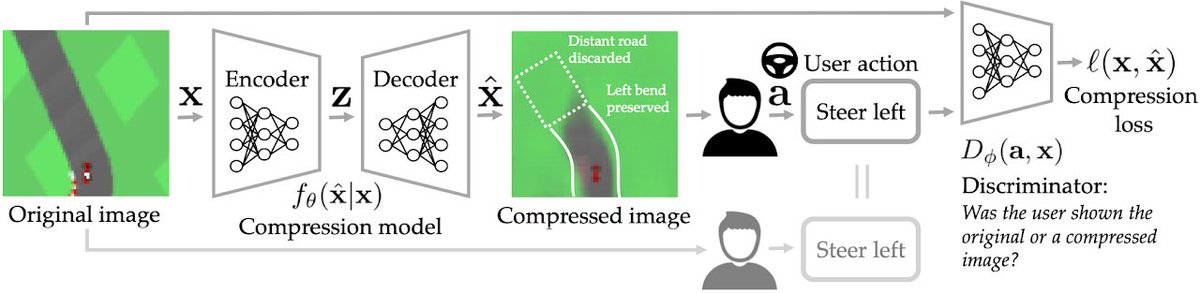
RAIL will be presenting a number of exciting late breaking poster results at the RL4RealLife WS #ICML2021 (8 pm PT today!): sites.google.com/view/RL4RealLi…
Algorithms for real-world RL w/ mobile manipulators, lifelong meta-learning methods, principled multi-task data sharing.
A thread:
Algorithms for real-world RL w/ mobile manipulators, lifelong meta-learning methods, principled multi-task data sharing.
A thread:
We'll show how RL can control robots that learn to clean up a room, entirely in the real world. By Charles Sun, @ColinearDevin, @abhishekunique7, @jendk3r, @GlenBerseth. 

We'll present CoMPS, an algorithm for online continual meta-learning, where an agent meta-learns tasks one by one, with each task accelerating future tasks. By @GlenBerseth, WilliamZhang365, @chelseabfinn 

We'll also present conservative data sharing (CDS), a new algorithm that provides a principled way to select which data to share between tasks in offline RL to minimize distributional shift! CDS will also be presented 6 pm PT Sat in the RL theory WS: icml.cc/virtual/2021/w… 

• • •
Missing some Tweet in this thread? You can try to
force a refresh