*Towards Domain-Agnostic Contrastive Learning*
#ICML 2021 by @vikasverma1077 @lmthang Kawaguchi @hieupham789 @quocleix
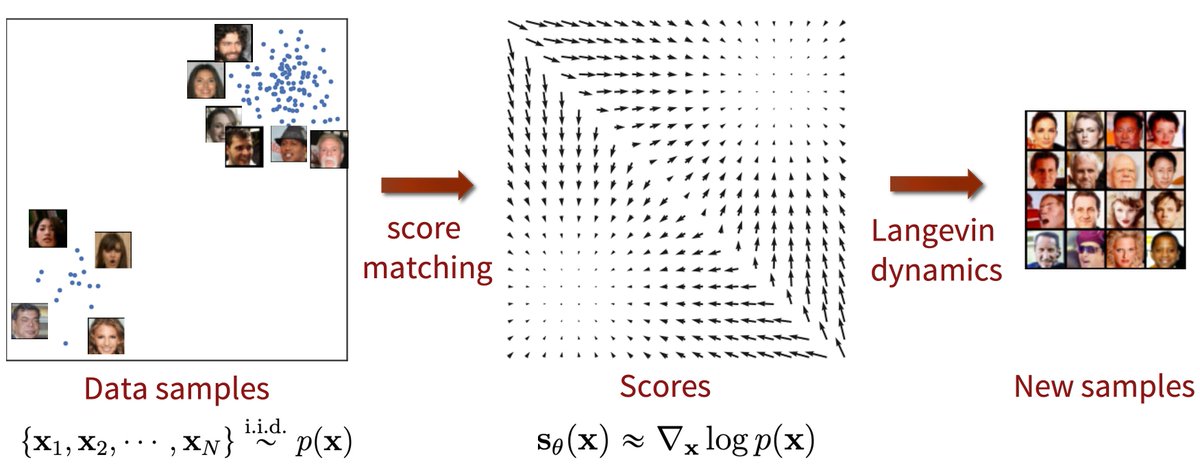
Here's an interesting question: can we do self-supervised learning if we know *nothing* about the domain we are operating on?
/n
#ICML 2021 by @vikasverma1077 @lmthang Kawaguchi @hieupham789 @quocleix
Here's an interesting question: can we do self-supervised learning if we know *nothing* about the domain we are operating on?
/n

The solution they propose is fascinatingly simple: create a positive pair by moving a short distance towards another point (mixup).
The intuition being that this captures the manifold along which the data resides.
For graphs/sequences, do mixup on a fixed-length embedding.
/n
The intuition being that this captures the manifold along which the data resides.
For graphs/sequences, do mixup on a fixed-length embedding.
/n

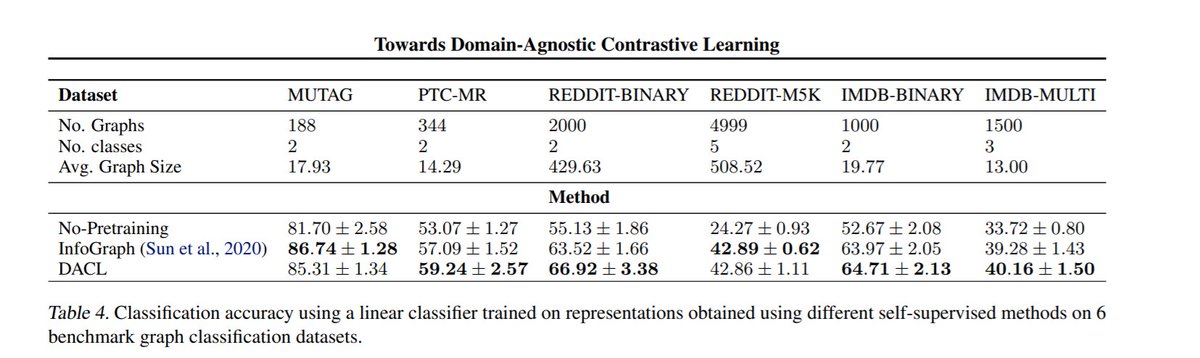
The theoretical analysis shows that this acts similarly to a form of regularization, and the experiments are quite impressive.
Paper: arxiv.org/abs/2011.04419
Paper: arxiv.org/abs/2011.04419
• • •
Missing some Tweet in this thread? You can try to
force a refresh