
1/
Get a cup of coffee.
In this thread, I'll show you how the P/E ratio of a portfolio is related to the P/E ratios of its individual stocks.
The math here is beautiful. It involves harmonic means and a super elegant theorem known as the Cauchy-Schwarz Inequality.
Get a cup of coffee.
In this thread, I'll show you how the P/E ratio of a portfolio is related to the P/E ratios of its individual stocks.
The math here is beautiful. It involves harmonic means and a super elegant theorem known as the Cauchy-Schwarz Inequality.
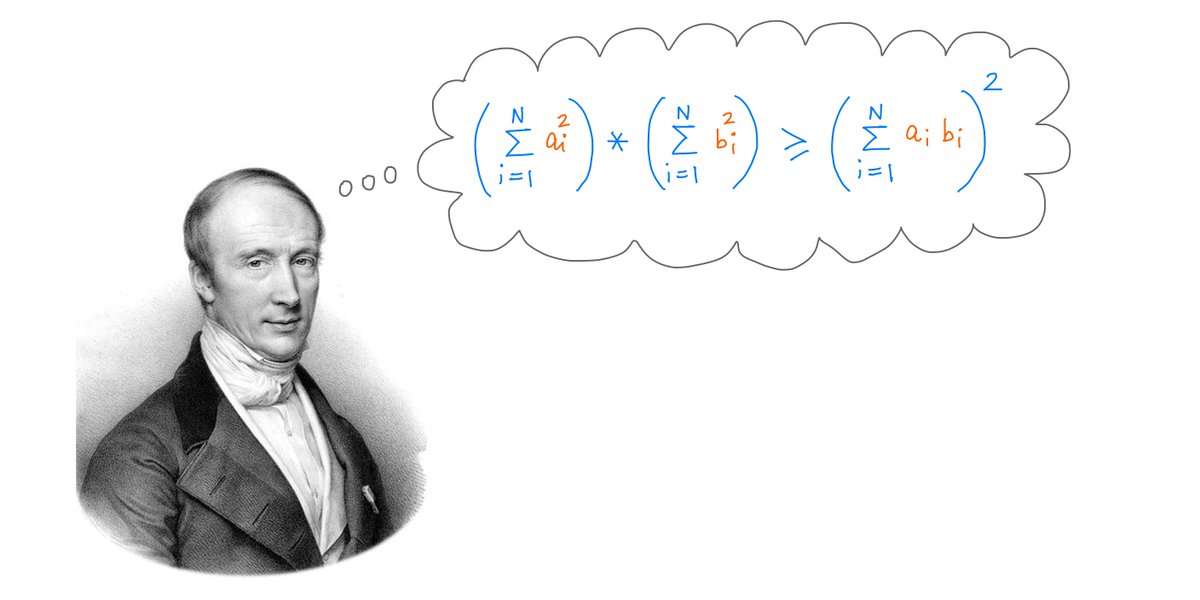
2/
Earlier this week, I conducted a poll where I asked this question about P/E ratios.
Over 6,000 people responded.
Unfortunately, most of them got the answer wrong.
That's why I'm writing this thread. To (hopefully) correct some of the misconceptions that led people astray.
Earlier this week, I conducted a poll where I asked this question about P/E ratios.
Over 6,000 people responded.
Unfortunately, most of them got the answer wrong.
That's why I'm writing this thread. To (hopefully) correct some of the misconceptions that led people astray.

3/
To answer questions like this, it's always a good idea to go back to first principles.
In this case, we should ask ourselves: what exactly does a P/E ratio capture?
To answer questions like this, it's always a good idea to go back to first principles.
In this case, we should ask ourselves: what exactly does a P/E ratio capture?
4/
We know that the P in P/E stands for Price. In other words, the amount we need to pay to acquire an asset today.
And the E stands for Earnings. The amount earned by our asset in the last 1 year.
We know that the P in P/E stands for Price. In other words, the amount we need to pay to acquire an asset today.
And the E stands for Earnings. The amount earned by our asset in the last 1 year.
5/
Note: P/E ratios come in more than 1 flavor.
For the E part, some people use earnings during the *last* 1 year. This is called the *trailing* P/E ratio.
Others use an estimate of earnings during the *next* 1 year. This is called the *forward* P/E ratio.
Note: P/E ratios come in more than 1 flavor.
For the E part, some people use earnings during the *last* 1 year. This is called the *trailing* P/E ratio.
Others use an estimate of earnings during the *next* 1 year. This is called the *forward* P/E ratio.
6/
In this thread, we use *trailing* P/Es.
But as long as we're *consistent* -- ie, we choose a particular definition and stick to it throughout -- the precise P/E variant we use doesn't matter.
The math works out pretty much the same either way.
In this thread, we use *trailing* P/Es.
But as long as we're *consistent* -- ie, we choose a particular definition and stick to it throughout -- the precise P/E variant we use doesn't matter.
The math works out pretty much the same either way.
7/
The P/E ratio thus brings together the 2 fundamental considerations for investing in *any* asset: *price* and *value*.
1) Price: What we pay for the asset, and
2) Value: How much the asset earns for us each year (approximated by how much the asset earned *last* year).
The P/E ratio thus brings together the 2 fundamental considerations for investing in *any* asset: *price* and *value*.
1) Price: What we pay for the asset, and
2) Value: How much the asset earns for us each year (approximated by how much the asset earned *last* year).
8/
Clearly, the *less* we pay for an asset (*low* P),
and the *more* the asset earns for us each year (*high* E),
the *lower* our P/E ratio,
and the *higher* our return from buying the asset.
Clearly, the *less* we pay for an asset (*low* P),
and the *more* the asset earns for us each year (*high* E),
the *lower* our P/E ratio,
and the *higher* our return from buying the asset.
9/
Because of this *inverse* relationship between our P/E ratio and our investment return, it's useful to *invert* our P/E ratio.
This gives us our *earnings yield*.
Because of this *inverse* relationship between our P/E ratio and our investment return, it's useful to *invert* our P/E ratio.
This gives us our *earnings yield*.

10/
IF we buy an asset and hold it forever,
and IF this asset earns the same amount each year,
and IF all these earnings come to us as (tax-free) dividends each year,
THEN our return on this investment will *exactly* equal our earnings yield -- the inverse of our P/E ratio.
IF we buy an asset and hold it forever,
and IF this asset earns the same amount each year,
and IF all these earnings come to us as (tax-free) dividends each year,
THEN our return on this investment will *exactly* equal our earnings yield -- the inverse of our P/E ratio.
11/
That's why the P/E ratio is so useful. It's inverse (ie, earnings yield) determines the return we'll get from buying an asset.
But of course, there are some pretty BIG IFs in the previous tweet. Therein lie the pitfalls of the P/E ratio.
That's why the P/E ratio is so useful. It's inverse (ie, earnings yield) determines the return we'll get from buying an asset.
But of course, there are some pretty BIG IFs in the previous tweet. Therein lie the pitfalls of the P/E ratio.
12/
For example, suppose a company with 100M shares outstanding earned $1B last year. That's $1B / (100M shares) = $10 in Earnings Per Share (EPS).
Suppose this company trades at a 20 P/E (ie, 5% earnings yield).
That means each share is priced at (20 P/E) * ($10 EPS) = $200.
For example, suppose a company with 100M shares outstanding earned $1B last year. That's $1B / (100M shares) = $10 in Earnings Per Share (EPS).
Suppose this company trades at a 20 P/E (ie, 5% earnings yield).
That means each share is priced at (20 P/E) * ($10 EPS) = $200.
13/
If we buy $100K worth of shares in this company, that's $100K / ($200 per share) = 500 shares.
And last year, these 500 shares earned (500 shares) * ($10 EPS) = $5K.
In other words, we're shelling out $100K (P) to buy $5K worth of earnings (E).
If we buy $100K worth of shares in this company, that's $100K / ($200 per share) = 500 shares.
And last year, these 500 shares earned (500 shares) * ($10 EPS) = $5K.
In other words, we're shelling out $100K (P) to buy $5K worth of earnings (E).
14/
That's what a 20 P/E -- or equivalently, a 5% earnings yield -- means.
IF these earnings remain stable, and IF they come to us as dividends each year, we can expect to get a 5% annualized pre-tax return (IRR) on our $100K investment.
That's what a 20 P/E -- or equivalently, a 5% earnings yield -- means.
IF these earnings remain stable, and IF they come to us as dividends each year, we can expect to get a 5% annualized pre-tax return (IRR) on our $100K investment.
15/
With this background, it's easy to see that the equal-weighted portfolio in the poll question above has a P/E ratio of approximately 13.33.
It's because the portfolio was built by shelling out $200K (P) for $15K worth of earnings (E).
With this background, it's easy to see that the equal-weighted portfolio in the poll question above has a P/E ratio of approximately 13.33.
It's because the portfolio was built by shelling out $200K (P) for $15K worth of earnings (E).

16/
So, even though the *stocks* in the portfolio have an "average" P/E of 15, the *portfolio* has a P/E of only ~13.33.
This is because, when we combine stocks into a portfolio, it's their *earnings yields* that get averaged, not their P/E ratios.
So, even though the *stocks* in the portfolio have an "average" P/E of 15, the *portfolio* has a P/E of only ~13.33.
This is because, when we combine stocks into a portfolio, it's their *earnings yields* that get averaged, not their P/E ratios.
17/
When we encounter surprising results like this, it's a good idea to run some "extreme" numbers and see what happens.
For example, what if we equal-weight a 10 P/E stock with a 190 P/E stock -- so their "average" P/E is a hefty (10 + 190)/2 = 100?
When we encounter surprising results like this, it's a good idea to run some "extreme" numbers and see what happens.
For example, what if we equal-weight a 10 P/E stock with a 190 P/E stock -- so their "average" P/E is a hefty (10 + 190)/2 = 100?
18/
In this case, our portfolio's P/E turns out to be just 19.
Clearly, the 10 P/E stock plays a *much* bigger role in deciding our portfolio's overall P/E than the 190 P/E stock -- even though both stocks are weighted equally in the portfolio!
In this case, our portfolio's P/E turns out to be just 19.
Clearly, the 10 P/E stock plays a *much* bigger role in deciding our portfolio's overall P/E than the 190 P/E stock -- even though both stocks are weighted equally in the portfolio!

19/
If we just examine the math above, it's easy to see why.
It's because most of the portfolio's *earnings* come from the 10 P/E stock.
Compared to these earnings, the earnings produced by the 190 P/E stock are miniscule.
If we just examine the math above, it's easy to see why.
It's because most of the portfolio's *earnings* come from the 10 P/E stock.
Compared to these earnings, the earnings produced by the 190 P/E stock are miniscule.
20/
More generally, the P/E ratio of an equal-weighted N-stock portfolio is the *harmonic* mean of the P/E ratios of the individual stocks.
NOT their arithmetic mean (or common average).
Here's the math to prove it:
More generally, the P/E ratio of an equal-weighted N-stock portfolio is the *harmonic* mean of the P/E ratios of the individual stocks.
NOT their arithmetic mean (or common average).
Here's the math to prove it:

21/
This *harmonic* mean gives us a BIG clue.
See, there's this super important theorem in math called the Cauchy-Schwarz Inequality.
And this inequality tells us that the harmonic mean of *any* set of positive numbers can never exceed their arithmetic mean.
Proof:

This *harmonic* mean gives us a BIG clue.
See, there's this super important theorem in math called the Cauchy-Schwarz Inequality.
And this inequality tells us that the harmonic mean of *any* set of positive numbers can never exceed their arithmetic mean.
Proof:


22/
This means we can take as many stocks as we like and build an equal-weighted portfolio of them.
As long as each stock has positive earnings, our portfolio's P/E will *never* exceed the "average" P/E of our individual stocks.
Cauchy-Schwarz *guarantees* this. How cool!
This means we can take as many stocks as we like and build an equal-weighted portfolio of them.
As long as each stock has positive earnings, our portfolio's P/E will *never* exceed the "average" P/E of our individual stocks.
Cauchy-Schwarz *guarantees* this. How cool!
23/
And there's more! Our portfolio doesn't even have to be equal-weighted.
We can give each stock whatever weight we like in the portfolio.
And the portfolio's P/E is *still* guaranteed never to exceed the weighted average P/E of our individual stocks.

And there's more! Our portfolio doesn't even have to be equal-weighted.
We can give each stock whatever weight we like in the portfolio.
And the portfolio's P/E is *still* guaranteed never to exceed the weighted average P/E of our individual stocks.


24/
There are 2 key lessons to take away from this thread.
Key lesson 1. Approach problems from first principles.
Starting at the basics (what is a P/E ratio?) and reasoning from there, most of us could have solved the poll question correctly. But ~62% of us got it wrong.
There are 2 key lessons to take away from this thread.
Key lesson 1. Approach problems from first principles.
Starting at the basics (what is a P/E ratio?) and reasoning from there, most of us could have solved the poll question correctly. But ~62% of us got it wrong.
25/
Key lesson 2. Knowledge of math helps us see all kinds of non-obvious connections.
I've experienced this time and again.
I studied harmonic means and the Cauchy-Schwarz Inequality in calculus class. But here I am, connecting these concepts to P/E ratios!
Key lesson 2. Knowledge of math helps us see all kinds of non-obvious connections.
I've experienced this time and again.
I studied harmonic means and the Cauchy-Schwarz Inequality in calculus class. But here I am, connecting these concepts to P/E ratios!
26/
Also, math fluency lets us become more discerning consumers of news, analysis, and information. Doing calculations becomes second nature to us, which makes us harder to fool.
For example, does 49 green ticks in 50 boxes really equal 95%? 😀
Cc: @billmaher
Also, math fluency lets us become more discerning consumers of news, analysis, and information. Doing calculations becomes second nature to us, which makes us harder to fool.
For example, does 49 green ticks in 50 boxes really equal 95%? 😀
Cc: @billmaher

27/
I'd also like to give a shout out to @ChrisBloomstran and @AlbertBridgeCap.
It was their exchange on harmonic means and P/E ratios that inspired me to write this thread.
I'd also like to give a shout out to @ChrisBloomstran and @AlbertBridgeCap.
It was their exchange on harmonic means and P/E ratios that inspired me to write this thread.

28/
If you're still with me, thank you very much!
I love seeing math ideas like harmonic means show up unexpectedly in investing calculations. And I hope this thread gave you an appreciation for this sort of thing as well.
Please stay safe. Enjoy your weekend!
/End
If you're still with me, thank you very much!
I love seeing math ideas like harmonic means show up unexpectedly in investing calculations. And I hope this thread gave you an appreciation for this sort of thing as well.
Please stay safe. Enjoy your weekend!
/End
• • •
Missing some Tweet in this thread? You can try to
force a refresh












