#Julia言語 100以下の素数
(a->a[a.∉(a*a',)])(2:100)
これを理解すれば、色々理解できたことになる。
九九の表は (1:9)*(1:9)' で作れる。
∉ は \notin TAB で入力できる。
a.∉(a*a',)の代わりにa.∉Ref(a*a')と書くことが多い。
実験するときには
a = 2:100
a[a.∉(a*a',)]
を試すとよい。
(a->a[a.∉(a*a',)])(2:100)
これを理解すれば、色々理解できたことになる。
九九の表は (1:9)*(1:9)' で作れる。
∉ は \notin TAB で入力できる。
a.∉(a*a',)の代わりにa.∉Ref(a*a')と書くことが多い。
実験するときには
a = 2:100
a[a.∉(a*a',)]
を試すとよい。

#Julia言語 解説
a = 2:100
のとき、aは2,3,4,...,100が縦に並んでいるベクトル扱いになる。
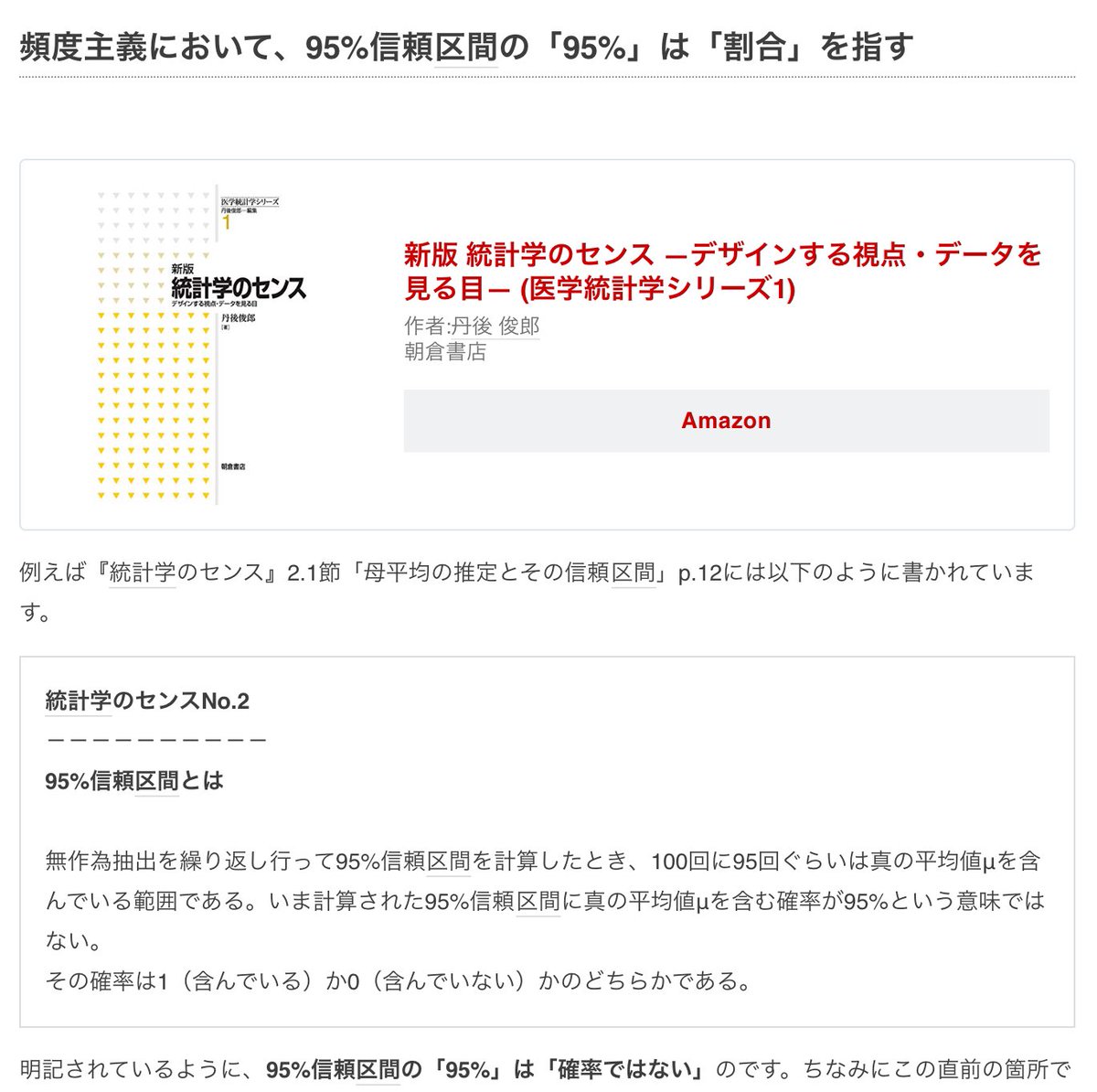
a'はaの転置で、横ベクトル扱いされる。
a*a' は通常の線形代数によって、2,3,4,...,100の2つの数の積を並べた99×99行列になる。続く
a = 2:100
のとき、aは2,3,4,...,100が縦に並んでいるベクトル扱いになる。
a'はaの転置で、横ベクトル扱いされる。
a*a' は通常の線形代数によって、2,3,4,...,100の2つの数の積を並べた99×99行列になる。続く

#Julia言語 100以下の素数全体は、a = 2:100 に含まれる数で行列 a*a' に含まれないものの全体に一致する。
a .∉ (a*a',) は a の各要素 k に写像 k ↦ k ∉ a*a' を作用させた結果になる。真偽値達のBitVectorになる。続く
a .∉ (a*a',) は a の各要素 k に写像 k ↦ k ∉ a*a' を作用させた結果になる。真偽値達のBitVectorになる。続く

#Julia言語 行列 a*a' をタプルを作る ( ,) で囲んでいるのは dot-syntax によるブロードキャスト(要素単位での作用)から保護するため。
a .∉ (a*a',) は a の中での素数の場所でtrueにそうでない場所でfalseになっている。
a[a .∉ (a*a',)] は a から素数だけを取り出す操作になっている。
a .∉ (a*a',) は a の中での素数の場所でtrueにそうでない場所でfalseになっている。
a[a .∉ (a*a',)] は a から素数だけを取り出す操作になっている。

#Julia言語 「ドット記法によるブロードキャストのときに、配列様のモノをスカラーとして振る舞わせるにはどうすればよいか?」はJuliaでのよくある質問の1つ。
多くの人がRef( )で包むという解決策を採用しており、このスレッドではタプルを作る( ,)で包む処方箋を採用した。
多くの人がRef( )で包むという解決策を採用しており、このスレッドではタプルを作る( ,)で包む処方箋を採用した。

#Julia言語
a = 2:100 の具象型はUnitRange{Int64}
さらにそれは a isa AbstractVector{Int64} をみたす。
AbstractVector型のオブジェクトは縦ベクトル扱いになる。
レンジがそのまま縦ベクトル扱いされる。配列に変換してメモリの無駄遣いをする必要はない。
a = 2:100 の具象型はUnitRange{Int64}
さらにそれは a isa AbstractVector{Int64} をみたす。
AbstractVector型のオブジェクトは縦ベクトル扱いになる。
レンジがそのまま縦ベクトル扱いされる。配列に変換してメモリの無駄遣いをする必要はない。

#Julia言語 a' は LinearAlgebra.Adjoint 型になり、横ベクトル扱いされる。 
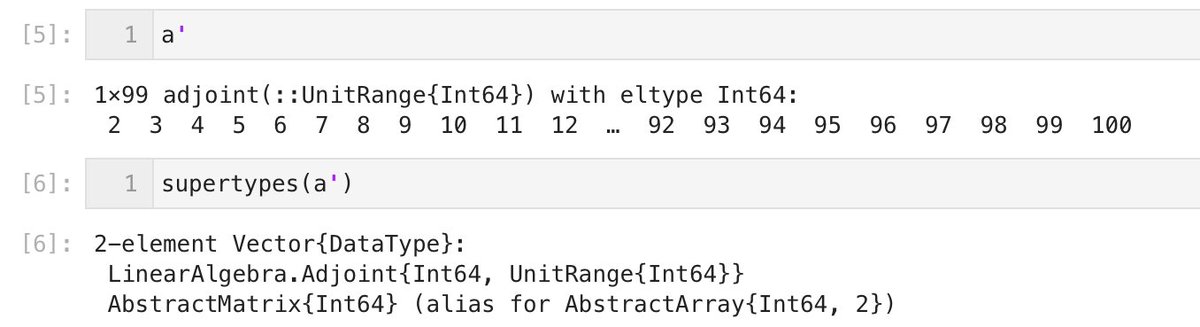
#Julia言語 a .∉ (a*a',) はBitVector型になり、AbstractVector型に属し、真偽値の縦ベクトル扱いされる。 
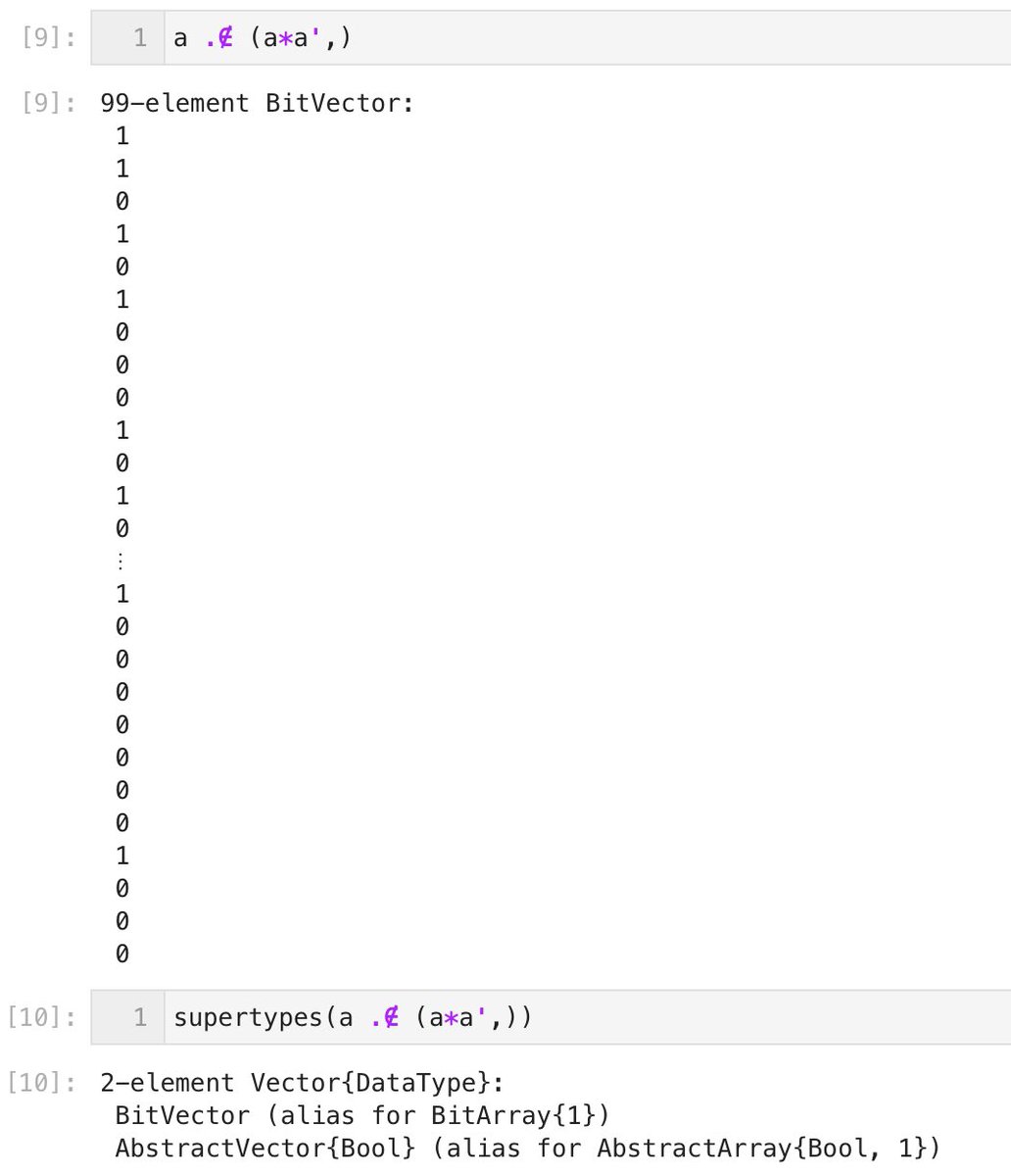
#Julia言語 a[a .∉ (a*a',)] はVector{Int64}型になり、AbstractVector型に属する。
一般にAbstractVector型に属するオブジェクトは縦ベクトル扱いされる。
一般にAbstractVector型に属するオブジェクトは縦ベクトル扱いされる。

#Julia言語
a = 2:100; a[a.∉(a*a',)]
にはJuliaでよく使う基本的な事柄が詰め込まれており、理解する価値が十分にあると思う。
これで100以下の素数全体が得られる。
typeof, supertype, dump の使い方もついでに覚えてしまうと、「夜道で迷うこと」も少なくなるだろう。
a = 2:100; a[a.∉(a*a',)]
にはJuliaでよく使う基本的な事柄が詰め込まれており、理解する価値が十分にあると思う。
これで100以下の素数全体が得られる。
typeof, supertype, dump の使い方もついでに覚えてしまうと、「夜道で迷うこと」も少なくなるだろう。
#Julia言語 添付画像のコードは別スレで紹介したコード。
函数の引数の型がほとんど書かれておらず、Float64やInt64のような型名をユーザー側は全然入力していない。
函数の引数の型はJuliaにおける高速計算では書く必要がない。続く


函数の引数の型がほとんど書かれておらず、Float64やInt64のような型名をユーザー側は全然入力していない。
函数の引数の型はJuliaにおける高速計算では書く必要がない。続く
https://twitter.com/genkuroki/status/1436563724718907395



#Julia言語 しかし、このスレッドの内容を理解すれば裏で複雑な型システムが大活躍していることがわかる。
Juliaの計算が速いのはこの型システムのおかげ。
既存の遅いプログラミング言語をJulia並に速くするためには、Julia並の型システムを導入する必要があり、破壊的な変更が必要になるだろう。
Juliaの計算が速いのはこの型システムのおかげ。
既存の遅いプログラミング言語をJulia並に速くするためには、Julia並の型システムを導入する必要があり、破壊的な変更が必要になるだろう。
#Julia言語
(a->a[a.∉(a*a',)])(2:100)
含まれる内容:
* 無名函数
* ユニットレンジ
* ユニットレンジも縦ベクトルとみなされる
* 横ベクトルを転置で作れる
* かけ算で行列ができる
* ユニコード演算子
* ブロードキャスト
* ブロードキャストからの保護の( ,)
* BitVectorによるマスキング
(a->a[a.∉(a*a',)])(2:100)
含まれる内容:
* 無名函数
* ユニットレンジ
* ユニットレンジも縦ベクトルとみなされる
* 横ベクトルを転置で作れる
* かけ算で行列ができる
* ユニコード演算子
* ブロードキャスト
* ブロードキャストからの保護の( ,)
* BitVectorによるマスキング
• • •
Missing some Tweet in this thread? You can try to
force a refresh