Thread by @genkuroki

#Julia言語 グローバル変数Aを参照する

S(x) = S(A, x)

の類の函数の定義は計算効率重視なら避けるべき。

しかし、これができないと途方に暮れる人もいるかもしれない。

そういう人は

github.com/genkuroki/publ…

github.com/genkuroki/publ…

のスタイルをパクればよい。

https://twitter.com/genkuroki/status/1435976905111445509

#Julia言語

あと、初心者のうちは、内部コンストラクタを使わざるを得ない場合を除いて、内部コンストラクタを定義しない方が無難だと思う。要するに、初心者段階では

struct Foo{A, B}
a::A
b::B
function Foo(～) ～ new(a, b) end
end

のようにできるだけ書かないようにする。続く

#Julia言語 代わりに、単に

struct Foo{A, B}
a::A
b::B
end

と書くか、必要に応じて外部コンストラクタを

function Foo(～) ～ Foo(a, b) end

のように定義しておく。続く

#Julia言語 可能ならば、内部コンストラクタを使いたくない理由は、内部コンストラクタを定義すると、そうしなかった場合に自動的に定義されるデフォルトのコンストラクタが失われることです。

デバッグのときに不自由する場合があります。

#Julia言語 この辺の事情に疎い場合には、struct ～ end の間にコンストラクタを書かないことによって、デフォルトで定義されるコンストラクタを有効にしておいた方が無難だと思う。

(自己参照のような内部コンストラクタでなければできないことをする場合には、内部コンストラクタを使う。)

#Julia言語

struct Foo{A, B}
a::A
b::B
end

とするだけで、

Foo(a, b)

と

Foo{A, B}(a, b)

の2つのコンストラクタを使用できます。

内部コンストラクタの使用のようなリスクを伴う難しいことをする必要はない。

#Julia言語 あと、後で最適化によるスピードアップを試みる予定ならば、「表示しながら計算する函数」「ファイルに結果を保存しながら計算する函数」は書かない方がよいです。

計算するための函数と表示や保存の函数を分離して、計算のための函数単体でテストできるようにしておく必要があります。

「計算するための函数と表示や保存の函数を分離して、計算のための函数単体でテストできるようにしておく」だとか、「問題を記述するパラメータ群をグローバル変数達にべた書きしたりしない」というようなことは、#Julia言語 と無関係に常識になって欲しいです。

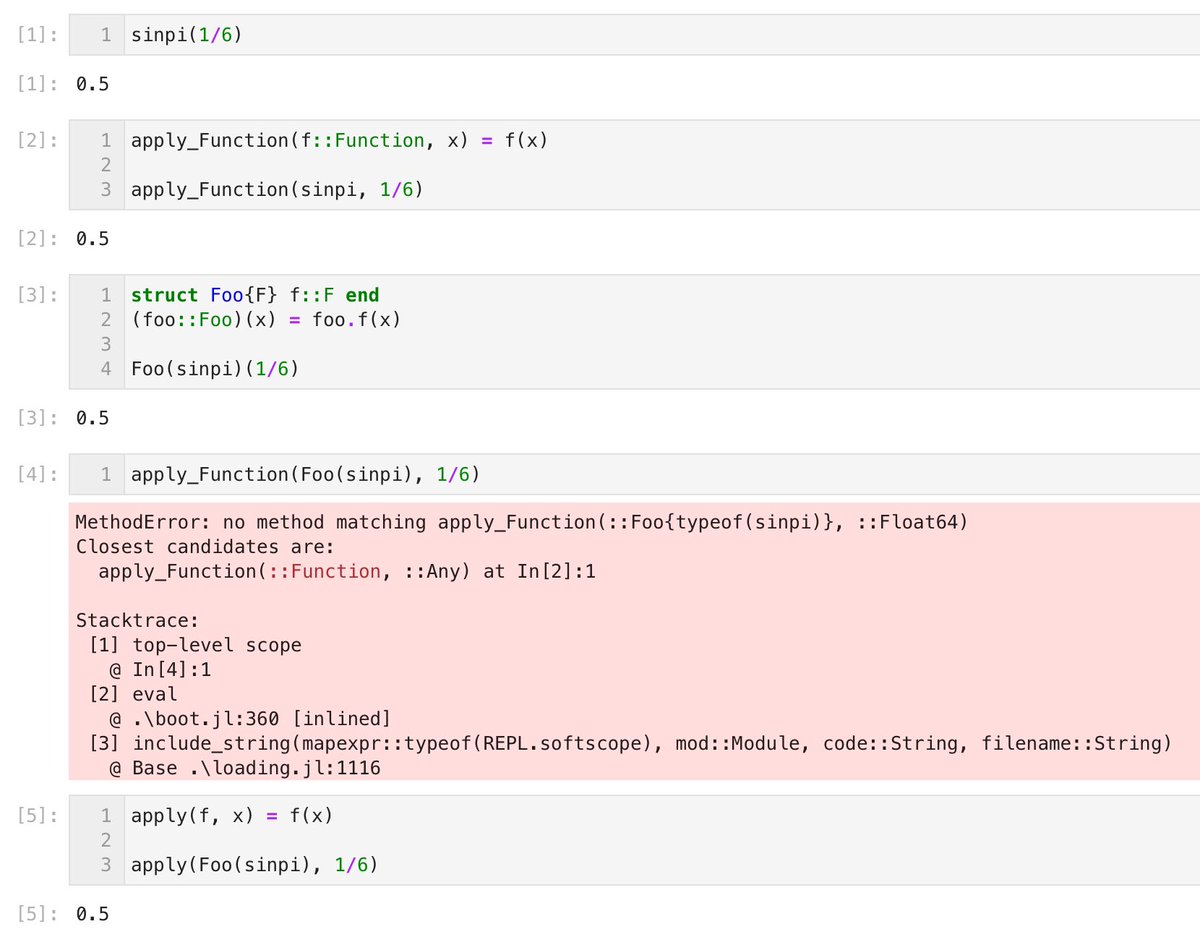
#Julia言語 函数を引数とする函数を

apply(f::Function, x) = f(x)

のように書くと、f(x)の形式で使えるオブジェクトの一部を引数として受け取れない函数が出来上がります。

添付画像のFoo(sinpi)はFunction型ではありません。

引数の型を書かずに、

apply(f, x) = f(x)

と書く方が勝ります。

#Julia言語

函数の引数の型を適切な範囲に制限することはかなり難しいです。

自信がなかったり、面倒だと思ったら、函数の引数の型を書かずに済ませるという手抜きが良い選択肢になる場合が多い。

#Julia言語 あと、mutable structを避けられるなら避けた方がお得。immutableなstructのmutableなフィールドの内容はいくらでも変更可能なので、mutable structが必要な場合が少ない。

struct Foo{A} a::A end
foo = Foo(zeros(3))
foo.a[1] = 99.9
push!(foo.a, 123.456)

のようなことをできます。

#Julia言語 次のように小さなmutable structを定義するのは損になることが多いです。

❌非推奨
mutable struct Point
x::Float64
y::Float64
end

似た例はBaseのComplex型(複素数型)。

Complex型はmutableでないstructで定義されています。

これを真似ればよい。
github.com/JuliaLang/juli…

#Julia言語 複素数と同じような感覚で使えるimmutableでサイズが固定されたベクトルは StaticArrays.jl で SVector という名で定義されています。

長さ30以下程度の短いベクトルの扱いでは非常にお勧め。

「3次元空間の点を動かす」のようなコードを書くときにはまずこれの使用を考える。

#Julia言語 で複素数値函数が欲しければ返り値がComplex型の函数のコードを書くのが普通ですが、それと同じような感覚で、n⪅30のとき、n次元ベクトル値函数が欲しければ返り値がSVector型の函数を書く。

Vector型を返り値にする場合と違って無駄なアロケーション発生を防げます。

#Julia言語 高次元ベクトルの時間発展を扱いたい場合の最適化では、作業領域として確保しておいたVectorを使い回すコードを書く必要が生じます。

使い回さずに素朴に書くとメモリ割り当てが増えて死ぬ。

アロケーションの節約はJuliaに限らず、最適化のイロハのイになる。

#Julia言語 低次元でStaticArrays.jlが便利なのは、行列とベクトルの積をSMatrixとSVectorで実装する場合も同様です。

具体例が

github.com/genkuroki/publ…

にある。

#Julia言語 SVectorの乱数生成は結構面倒な場合があります。無駄なアロケーションを避けることと、SVectorの長さを既知にしないと型不安定になってしまうことの2つが問題になる。

そのための面倒な場合の工夫が、既出の最新ノートブック

github.com/genkuroki/publ…

にあります。

#Julia言語 最初は面倒だと思うかもしれませんが、rand函数(randnでも同様)を、rand()の形式ではなく、乱数発生器をrngとするときの rand(rng) の形式で使うようにしておくと、後で乱数発生器を好きなものに変更可能になって便利です。

さらに、Julia v1.6.2だとrand(rng)の方が明らかに速いです。

#Julia言語 ベクトルの乱数を rand(n) または rand(rng, n) の形式で生成すると、メモリアロケーションが発生するので、ループの内側でそれらを使うことは避けたい。

using Randomし、ループの外側で長さnのベクトルtmpを用意しておいて、rand!(rng, tmp)を使うとよいです。

#Julia言語 を使い始める人達の多くが世間一般の中では相対的数学強者なので、最初から結構な複雑さを持つコードの最適化に挑戦する場合が多い。

それが結構罠で、シンプル過ぎると思われるような場合から出発しないと、一度に多くのことを学習しなければいけなくなって大変になる。私もそうでした。

#Julia言語 具体的には、常微分方程式の数値解法の場合には。Runge-Kuttaやleapfrogをやる前に、最単純なEuler法の最適化をやっておくとよいと思う。

際単純なEuler法もJuliaでの「最適化ゲーム」として十分に面白いです。

#Julia言語 最単純なオイラー法でも面白くなる理由は、Juliaでは函数の引数の型を書く必要がなくて、函数の実行時には、引数の型の組み合わせに最適化されたネイティブコードにコンパイルされて実行されるからです。

続く

#Julia言語 オイラー法の実装では、原則として函数の引数の型を一切書かずに、可能な限り広い場合に型安定になるコードを書くようにすれば、

　完全に同一のコード

で、

　実数値
　複素数値
　ベクトル値
　行列値
　幅を持った数値

などの場合にオイラー法を適用できるようになります。

#Julia言語 完全に同じコードで、Float64, Float32, Fliat128, BigFloat など様々な精度の浮動小数点数を扱えるようにすることは結構よい練習問題。

#Julia言語 「Float128の函数には q をつける」というような面倒ごとから完全に離脱できる。

引数の型を Float64 とかに決め打ちすることがどれだけ損であるかもわかる。

#Julia言語 で、オイラー法によるexp(x)の近似計算を実行すれば、完全に同一のコードで、xの型がFloat64, Float32, BigFloat, ComplexF64, Matrix{Float64}, Matrix{ComplexF64}, ...の場合の exp(x) の近似計算が可能になる。

しかも、各型ごとに別々に最適化されたネイティブコードが実行される！

#Julia言語 サイズが小さな行列の場合に限っては、SMatrix型の場合の方が速いことも確認できるだろう。

#Julia言語 個人的にずっとびっくりさせられ続けていることの1つは、「函数の引数の型を書かないこと」を嫌がる人達が結構いること。

引数の型を書かなくてもC並に速さで計算してくれるJuliaを使っているのに、引数の型を書かないと落ち着かないらしい。

この辺は「過学習」に問題だと思う。

https://twitter.com/genkuroki/status/1436321468376178701

#Julia言語 Juliaで函数の引数の型を十分な理解抜きに書くと、様々な問題が生じます。場合によっては思わぬバグ発生の原因になる。

色々理解していれば、「ドキュメント」として函数の引数の型を書いても害はないと思いますが、実際にはそうでもない。viewやSubStringでハマる人が続出するだろう。

#Julia言語

函数の引数に型を書くことを「コメント」の代わりに使うと、有害な副作用の問題を気にする必要がある。

有害な副作用を防ぐうまいやり方は、函数のdoc stringに函数に関するコメントを残しておくことです。REPLなどでの?で閲覧できるので、# を使ったコメントより便利です。

#Julia言語

"""
f(A, x)のAは行列でxはベクトルのつもり
"""
f(A, x) = A*x

と書いておくと、

?f

で

f(A, x)のAは行列でxはベクトルのつもり

が表示されるようになります。

doc stringを書いてくれているパッケージは使い易いです。そうじゃない主要パッケージも結構あってつらい。