Thread by @svpino

I need your help.

The doctor tested me, and I came back positive for a disease that infects 1 of every 1,000 people.

The test comes back positive 99% of the time if the person has the disease. About 2% of uninfected patients also come back positive.

Do I have the disease?

To answer this question, we need to understand why the doctor tested me in the first place.

If I had symptoms or if she suspected I had the disease for any reason, the analysis would be different.

But let's assume that the doctor tested 10,000 patients for no specific reason.

Many people replied using Bayes Theorem to solve this problem.

This is correct. But let's try to come up with an answer in a different—maybe more intuitive—way.

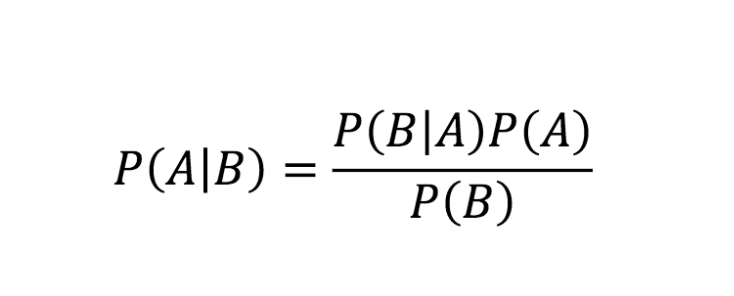
Here is what we currently know:

• Out of 1,000 people, 1 is sick
• Out of 100 sick people, 99 test positive
• Out of 100 healthy people, 98 test negative

Let's assume the doctor tested 100,000 people (including me):

• 100 of them are sick
• 99,900 of them are healthy

First, let's look at the group of the 100 sick patients:

• 99 of them will be diagnosed (correctly) as sick (99%)

• 1 of them is going to be diagnosed (incorrectly) as healthy (1%)

Now, let's look at the group of the 99,900 healthy patients:

• 97,902 of them will be diagnosed (correctly) as healthy. (98%)

• 1,998 of them will be diagnosed (incorrectly) as sick. (2%)

My test came back positive, so I belong to one of these two groups:

• The 99 people that are genuinely sick.

• The 1,998 people that are healthy but were diagnosed (incorrectly) as sick.

Basically, out of 2,097 positive results, 99 of them are genuinely sick while everyone else is not.

The probability that I have the disease is 99 / 2,097 ≈ 4.72%.

So, I'm probably not sick.