I just released a new chapter for the early access of my book, the Mathematics of Machine Learning!
This week, we are diving deep into the geometry of matrices.
What does this have to do with machine learning? Read on to find out. ↓
tivadar.gumroad.com/l/mathematics-…
This week, we are diving deep into the geometry of matrices.
What does this have to do with machine learning? Read on to find out. ↓
tivadar.gumroad.com/l/mathematics-…
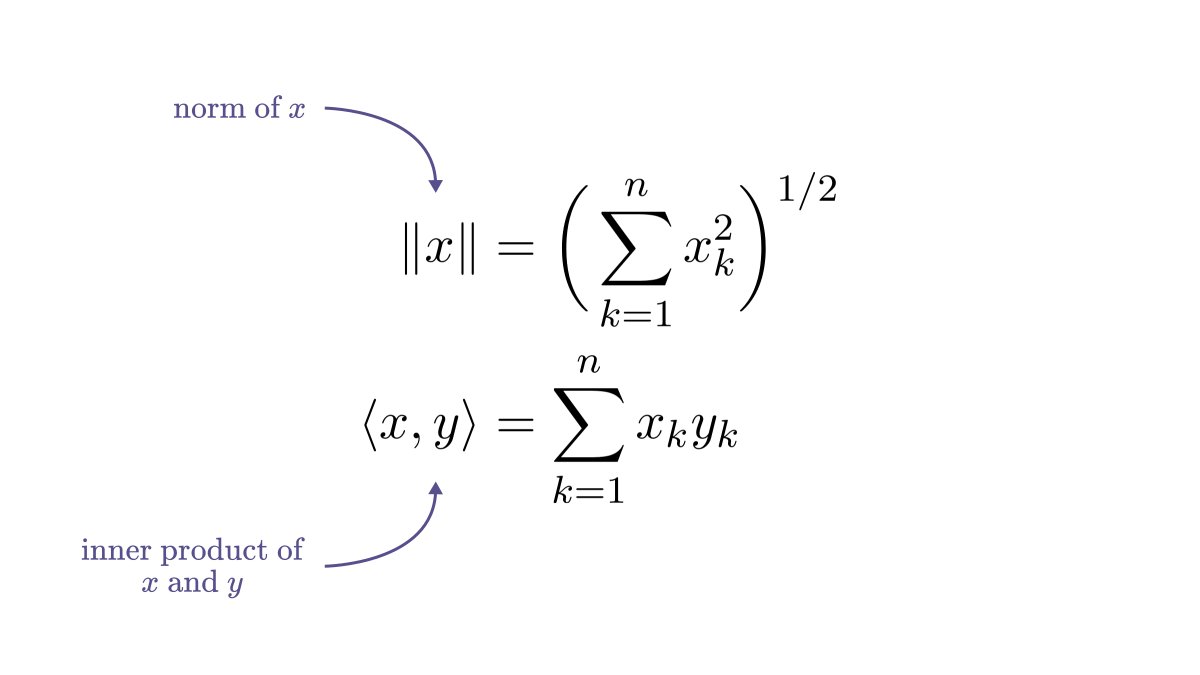
Matrices are the basic building blocks of learning algorithms.
Multiplying the data vectors with a matrix is equivalent to transforming the feature space. We think about this as a "black box", but there is a lot to discover.
For one, how they change the volume of objects.
Multiplying the data vectors with a matrix is equivalent to transforming the feature space. We think about this as a "black box", but there is a lot to discover.
For one, how they change the volume of objects.

This is described by the determinant of the matrix, which is given by
• how the transformation scales the volume,
• and how it changes the orientation of basis vectors.
The determinant is given by the formula below. I am a mathematician, and even I find this intimidating.
• how the transformation scales the volume,
• and how it changes the orientation of basis vectors.
The determinant is given by the formula below. I am a mathematician, and even I find this intimidating.

However, the determinant can be explained in terms of simple geometric concepts.
This new chapter takes this route, making determinants easy to understand. From motivation to applications, I am taking you through all the details.
This new chapter takes this route, making determinants easy to understand. From motivation to applications, I am taking you through all the details.
In the early access, I publish chapters as I write them.
Moreover, you get a personal hotline to me, where
• I help you out if you are stuck,
• and you can share your feedback with me.
This way, I can build the best learning resource for you.
tivadar.gumroad.com/l/mathematics-…
Moreover, you get a personal hotline to me, where
• I help you out if you are stuck,
• and you can share your feedback with me.
This way, I can build the best learning resource for you.
tivadar.gumroad.com/l/mathematics-…
• • •
Missing some Tweet in this thread? You can try to
force a refresh