#Julia言語
C++は避けるべき。
できあいの統計関連のライブラリやパッケージを主に使うなら、Rが多分良くて、Pythonも良いと思います。
サンプルコードでアルゴリズムも示したいならば、ほぼJulia一択だと思います。
実際、須山敦志さんはJuliaを早くから使い始めて大成功しているように見える。
C++は避けるべき。
できあいの統計関連のライブラリやパッケージを主に使うなら、Rが多分良くて、Pythonも良いと思います。
サンプルコードでアルゴリズムも示したいならば、ほぼJulia一択だと思います。
実際、須山敦志さんはJuliaを早くから使い始めて大成功しているように見える。
https://twitter.com/3colpenpines/status/1458505177862836226
#Julia言語
machine-learning.hatenablog.com/search?q=Julia
で須山さんによるJuliaを利用した確率統計の学び方を知ることができる。Juliaは高速かつ強力かつ気楽に使えるので、試しに自力実装するのに非常に向いている。
amazon.co.jp/dp/4065259800
Juliaで作って学ぶベイズ統計学 (KS情報科学専門書)
2021/11/26
須山敦志
machine-learning.hatenablog.com/search?q=Julia
で須山さんによるJuliaを利用した確率統計の学び方を知ることができる。Juliaは高速かつ強力かつ気楽に使えるので、試しに自力実装するのに非常に向いている。
amazon.co.jp/dp/4065259800
Juliaで作って学ぶベイズ統計学 (KS情報科学専門書)
2021/11/26
須山敦志
#統計 #Julia言語
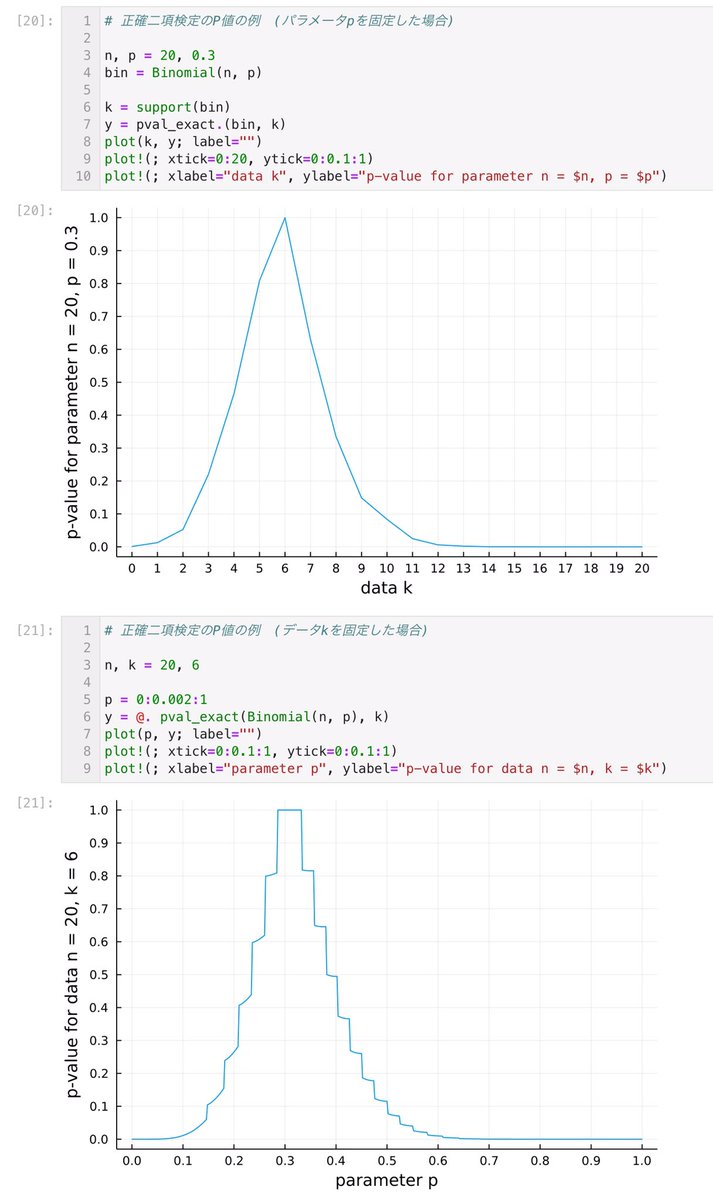
コインを20回投げたときの表が出る回数の分布は正規分布で近似される。
Juliaのコードがシンプルであること、確率分布を意味するオブジェクトを作って、確率函数、乱数、プロットで使えること、などに注目!
nbviewer.org/github/genkuro…


コインを20回投げたときの表が出る回数の分布は正規分布で近似される。
Juliaのコードがシンプルであること、確率分布を意味するオブジェクトを作って、確率函数、乱数、プロットで使えること、などに注目!
nbviewer.org/github/genkuro…



#統計 #Julia言語
2つの確率パラメータ(比率パラメータ)が等しい二項分布で生成れれたサンプルのZ統計量は近似的に標準正規分布に従う。
これは母比率が等しいことの検定の基本原理。
nbviewer.org/github/genkuro…
2つの確率パラメータ(比率パラメータ)が等しい二項分布で生成れれたサンプルのZ統計量は近似的に標準正規分布に従う。
これは母比率が等しいことの検定の基本原理。
nbviewer.org/github/genkuro…

#統計 #Julia言語 確率分布やプロットや零点を求めることについては汎用パッケージを利用しているが、P値函数や信頼区間函数をほぼ自前で実装しているのに、コードが非常にシンプルであったことに注目。
型名注釈は皆無だが、そのままでC, C++, Fortranと同程度の速さで計算してくれる。
型名注釈は皆無だが、そのままでC, C++, Fortranと同程度の速さで計算してくれる。
#統計 #Julia言語
以上のように、各種の確率分布を確率分布を意味するオブジェクトをコンピュータ上で扱うことによって勉強したり、自分でP値函数や信頼区間函数を実装したりして、確率統計について自習する目的にはJuliaが最適であることは十分に説得力がある主張だと思います。
以上のように、各種の確率分布を確率分布を意味するオブジェクトをコンピュータ上で扱うことによって勉強したり、自分でP値函数や信頼区間函数を実装したりして、確率統計について自習する目的にはJuliaが最適であることは十分に説得力がある主張だと思います。
#Julia言語
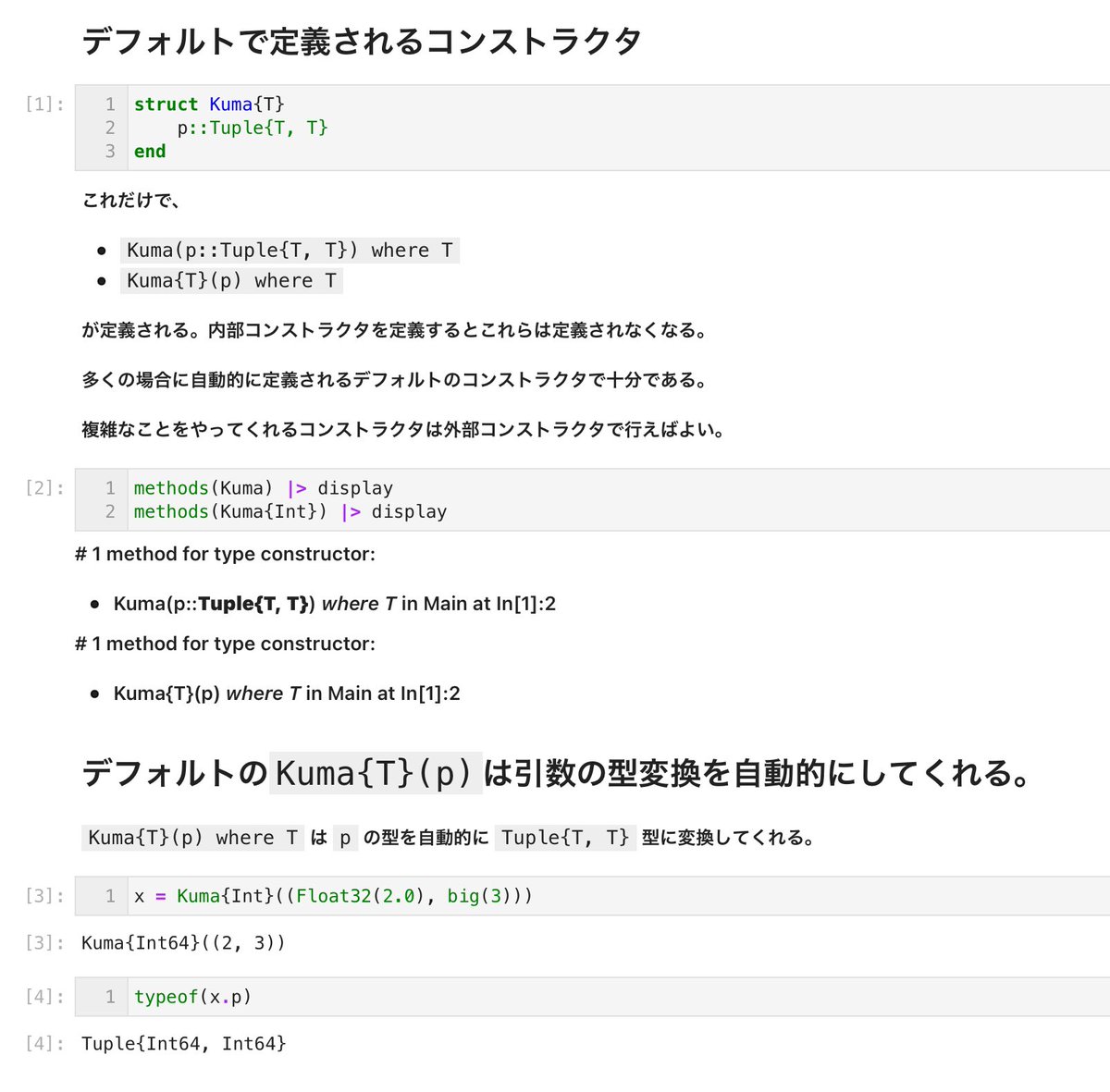
高速であって欲しい数値計算用のコードであっても型注釈を一切書かずに済ませられる気楽さが本領発揮されるのは以下のリンク先のような場面です。
数値計算のために使った函数をそのまま数式処理でも利用して欲しい公式を証明できてしまっています!
多重ディスパッチ万歳な感じ。
高速であって欲しい数値計算用のコードであっても型注釈を一切書かずに済ませられる気楽さが本領発揮されるのは以下のリンク先のような場面です。
数値計算のために使った函数をそのまま数式処理でも利用して欲しい公式を証明できてしまっています!
多重ディスパッチ万歳な感じ。
https://twitter.com/genkuroki/status/1459087926608859140
#統計 データkの値を固定してパラメータpの函数としてのP値函数のプロットをする利点は、信頼区間もそこから読み取れることです。
添付画像①ではデータがn=20回中k=6回成功のとき、成功確率pの95%信頼区間を赤線で示しています。
添付画像②にもn=20, k=6での95%信頼区間を赤線で示した。

添付画像①ではデータがn=20回中k=6回成功のとき、成功確率pの95%信頼区間を赤線で示しています。
添付画像②にもn=20, k=6での95%信頼区間を赤線で示した。


#統計 仮に自分が教科書として採用して「サンプルコードを実行したい。どうすればよいのか?」と相談されたときに、「C++の開発環境+gnuplotなどのインストール」まで面倒を見るのはかなり辛い。
Julia, Python, RのJupyterトリオなら無難。
Juliaについてはこのスレのサンプルコードを参照。
Julia, Python, RのJupyterトリオなら無難。
Juliaについてはこのスレのサンプルコードを参照。
https://twitter.com/3colpenpines/status/1458505177862836226
#統計
nbviewer.org/github/genkuro…
二項分布モデルの場合のデータkごとの信頼区間のプロットの仕方を変えた。
20回中k回成功というデータが得られたときの、成功確率の95%信頼区間をまとめてプロット。
nbviewer.org/github/genkuro…
二項分布モデルの場合のデータkごとの信頼区間のプロットの仕方を変えた。
20回中k回成功というデータが得られたときの、成功確率の95%信頼区間をまとめてプロット。

#統計 二項分布モデルの両側検定版P値函数の定義とジェネリックな信頼区間函数と二項分布モデルの信頼区間函数。
信頼係数1-αの信頼区間はP値函数pvalue(data, param)から
ci(data, α) = { param | pvalue(data, param) ≥ α }
で定義し、実装時には零点を求める函数で両端の位置を求めればよい。

信頼係数1-αの信頼区間はP値函数pvalue(data, param)から
ci(data, α) = { param | pvalue(data, param) ≥ α }
で定義し、実装時には零点を求める函数で両端の位置を求めればよい。


#統計 検定の理論は、「棄却されるデータの値の集合(棄却領域)」や理論的にはより便利な「各データの値ごとに棄却する確率の値を対応させる検定函数」で記述すると便利なのですが、実用的にはP値が圧倒的に使われており、初学者向けにはP値の説明も丁寧にしておいた方が無難。
#統計 P値はモデルのパラメータ値とデータの値の函数になることを押さえておくと、データに対する信頼係数1-αの信頼区間を、データが与えられているのでパラメータのみの函数とみなされるP値函数の値が有意水準α以上になるパラメータの値の集合として捉えることが可能になります。
#統計 これによって、データとパラメータの函数としてのP値函数を通して、有意水準αの検定と信頼度1-αの信頼区間が表裏一体の関係になっていることがクリアに理解できます。
そして、コンピュータでの実装もそれによって抽象化できて易しくなる。
上の方では #Julia言語 でその実演をやっています。
そして、コンピュータでの実装もそれによって抽象化できて易しくなる。
上の方では #Julia言語 でその実演をやっています。
#統計 棄却領域や検定函数を使う検定の定式化の御利益は、完備十分統計量を用いた一様最強力不偏検定の構成法の類の理論的な議論をできるようになることだと思います。実践的には厳密に不偏な検定のみにこだわるのは不便なので、個人的には初学者向けの解説ではP値函数がよいと思います。
#統計 Rのような統計ソフトの出力結果はP値やP値函数から作った信頼区間だったりすることが多いので、それらに関する知識がないと実践的でなくなってしまいます。
#統計 添付画像は、20回中6回成功というデータが得られたときの、二項分布モデルのP値のグラフ。横軸は二項分布モデル内での成功確率のパラメータpの値です。モデル内成功確率pを決めるごとに、そのP値が決まる。
それによって信頼区間(conf. int.)もグラフのように決まる。
nbviewer.org/github/genkuro…
それによって信頼区間(conf. int.)もグラフのように決まる。
nbviewer.org/github/genkuro…

#統計 データの値とモデルのパラメータ値の組にP値を対応させるP値函数の明示的な定義は入門書では行われていないのですが、定義していなくても検定と信頼区間を扱っていれば実質的に扱っています。
そのグラフを色々描いて様子を見ると「百聞は一見に如かず」で直観的な理解が得られます。
そのグラフを色々描いて様子を見ると「百聞は一見に如かず」で直観的な理解が得られます。

#Julia言語 に限らず、PythonでもRでも、確率統計学習用のサンプルコードを公開するときに、我々が覚悟しておくべきことは、
計算のためのサンプルコードの作成以上に
視覚化のためのサンプルコードの作成の方が
大変になってしまうこと
プロットの仕方を学ぶことのコストは非常に高い。
計算のためのサンプルコードの作成以上に
視覚化のためのサンプルコードの作成の方が
大変になってしまうこと
プロットの仕方を学ぶことのコストは非常に高い。
https://twitter.com/3colpenpines/status/1458505177862836226
確率統計がらみの視覚化のサンプルコードを公開している分量において、私は日本語圏の中でも相当な上位に入ると思われます。
ただし主に使っているのは #Julia言語
私のtwilogでの検索を私自身がよく使っている
↓
twilog.org/genkuroki/sear…
ただし主に使っているのは #Julia言語
私のtwilogでの検索を私自身がよく使っている
↓
twilog.org/genkuroki/sear…
• • •
Missing some Tweet in this thread? You can try to
force a refresh