¡Vega, que nos vamos! Hoy voy a empezar en la imagen de la izquierda y voy a acabar en la imagen de la derecha. Si no te lo crees del todo, ¡#Hilo va!
#puentes, #Ingeniería , #estructuras, #bridges , #Engineering, #Structures #NoSoloPuentes
#puentes, #Ingeniería , #estructuras, #bridges , #Engineering, #Structures #NoSoloPuentes
Aquí tenéis un cubo en un llamado “equilibrio inestable”. Claro, el cubo volcará a poco que sufra una leve acción lateral.
El mismo cubo con un apoyo excéntrico está en desequilibrio, no cabe duda.
Ahora es cuando viene un voluntari@ a ejercer sobre el cubo un empuje lateral que lo estabilice. El equilibrio pasa a ser estable.
Este mismo voluntari@ puede hacer sobre el cubo el mismo efecto estabilizador tirando, en vez de empujando, del mismo.
Nuestro voluntari@, un ingenier@ aburrido, ha encontrado formas algo más enrevesadas de poner el cubo en equilibrio. T1 y E1 son tirantes en tensión. B1 es una biela o puntal en compresión. C1 también es una biela comprimida implícita en el cubo.
Nuestro voluntari@, que se ha cansado, nos dice amablemente que nos apañemos nosotros. Es por eso que vamos a anclar el tirante E1 al suelo. Gracias por tu ingenio 🤝, a partir de aquí seguimos nosotros solos.
Lo cierto es que estamos ante una estructura muy estable.
Ahora podría replicar esta estructura apilándola sobre si misma.
Ahora podría replicar esta estructura apilándola sobre si misma.
Una vez más!
No pares, sigue, sigue! 🎶
Esto es adictivo! Paremos aquí. ;-)
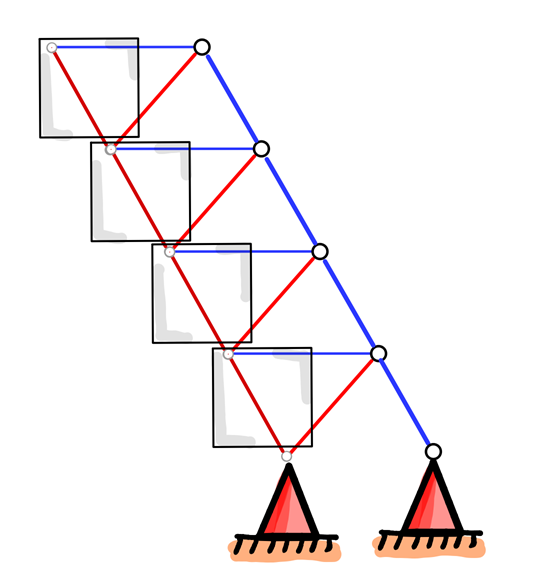
Nos ha quedado una estructura curiosa formada por 5 cubos apilados unos sobre otros.
Nos ha quedado una estructura curiosa formada por 5 cubos apilados unos sobre otros.
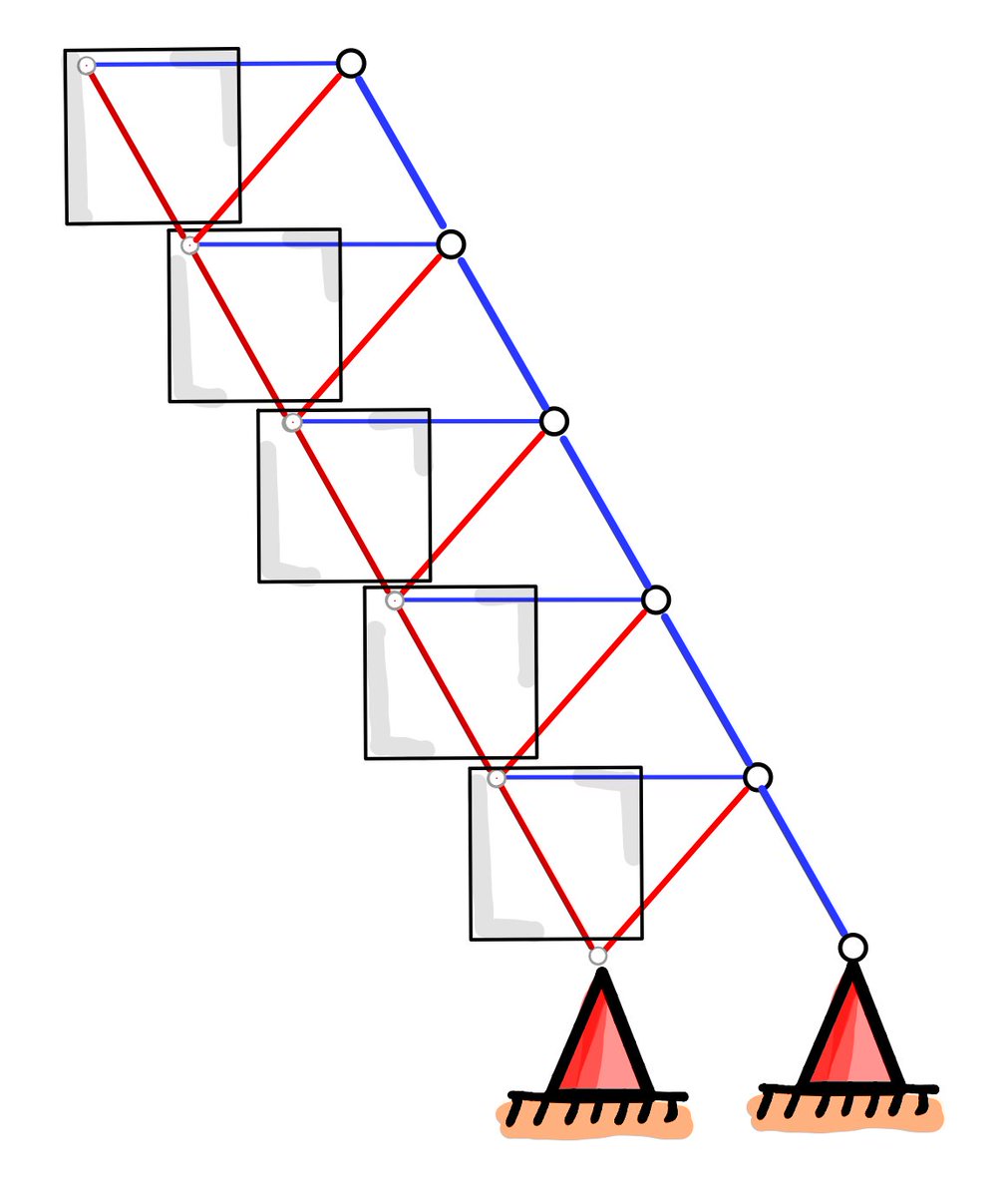
Ya sé que no hace falta, pero bien podría alargar el primer tramo de “espina dorsal”. Estamos de acuerdo en que el equilibrio de la estructura no cambia en nada.
En un momento de inspiración se nos ocurre alargar el apoyo triangular de la izquierda haciendo de él un prominente cono.
Hasta aquí los fundamentos estructurales de una escultura de #calatrava que podéis visitar en @esbaluardmuseu de #PalmaDeMallorca.
Esto es una parada intermedia. Tomad un respiro, seguimos!
Esto es una parada intermedia. Tomad un respiro, seguimos!
por cierto, foto de mi amigo @TiloBehrmann
Nuestro espíritu inquieto nos lleva a seguir indagando sobre estos equilibrios. Esta estructura, fruto del apilamiento sucesivo de cubos, no es más que una ménsula cuyo peso excéntrico P0 se equilibra gracias a los anclajes en cimentación.
Ahora voy a prescindir del apoyo derecho 😱. Tranquilos, es solo un dibujo.
La intención es apilar cubos en el lado derecho de la estructura hasta conseguir que el peso del conjunto se equilibre.
La intención es apilar cubos en el lado derecho de la estructura hasta conseguir que el peso del conjunto se equilibre.
El equilibrio solo ocurrirá cuando el peso del conjunto pase por el apoyo, es decir, que la distancia "di" tienda a 0. En la imagen, las fases 2 y 3 de nuestra búsqueda del equilibrio. El momento volcador que resta por equilibrar tiende a 0 a medida que apilamos más cubos.
Ya lo tenemos. hemos conseguido el equilibrio.
¡No te muevas, maricarmen!
¡No te muevas, maricarmen!
Hazme foto!
Para equlibrar el sistema frente a cargas desestabilizadoras diferentes al peso de la estructura, bien podría poner un apoyo en el extremo derecho de la misma. En estado permanente, la reacción en este apoyo es nula.
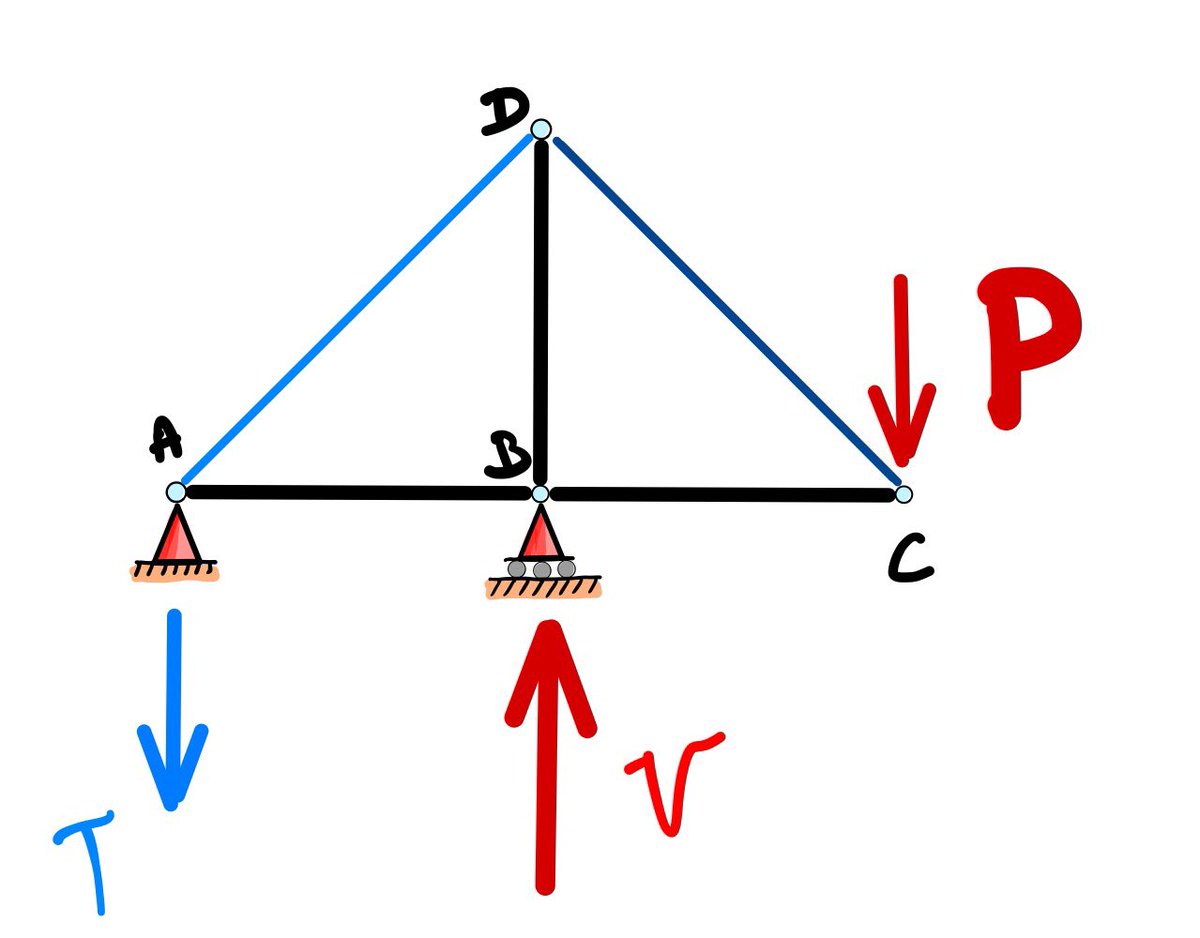
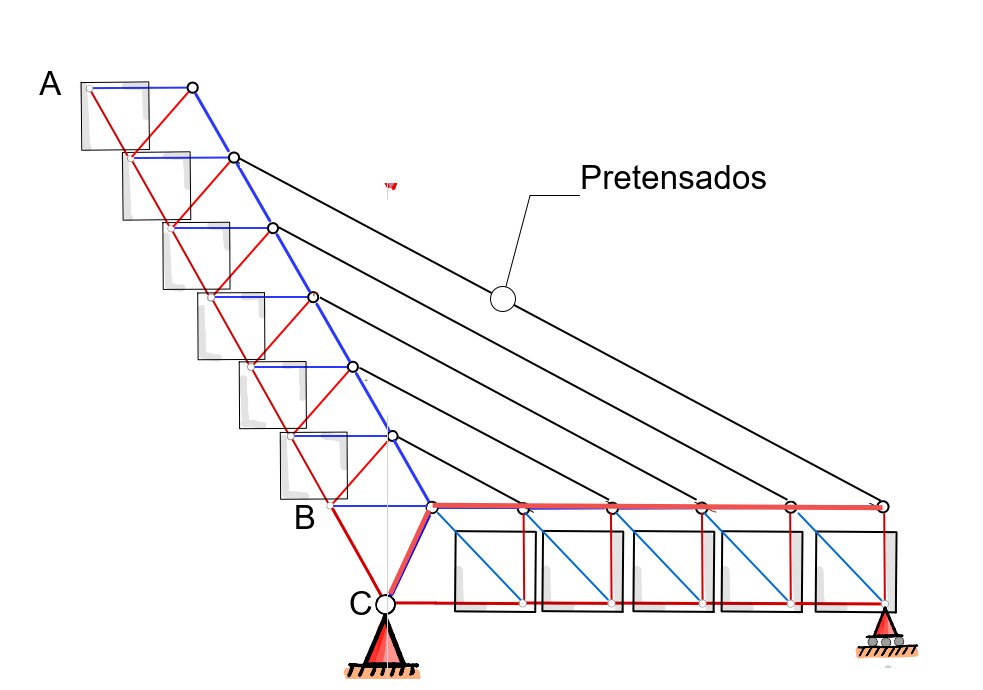
Ahora la estructura puede recibir cargas exteriores. La reacción en el apoyo derecho será, ahora sí, distinta de cero. Para que el mástil colabore en la resistencia del paso de la carga exterior, hemos añadido unos cables vinculando ambos lados de la estructura.
Hace un rato que sabéis que estoy ilustrando de una manera simplificada el puente del Alamillo en #Sevilla!
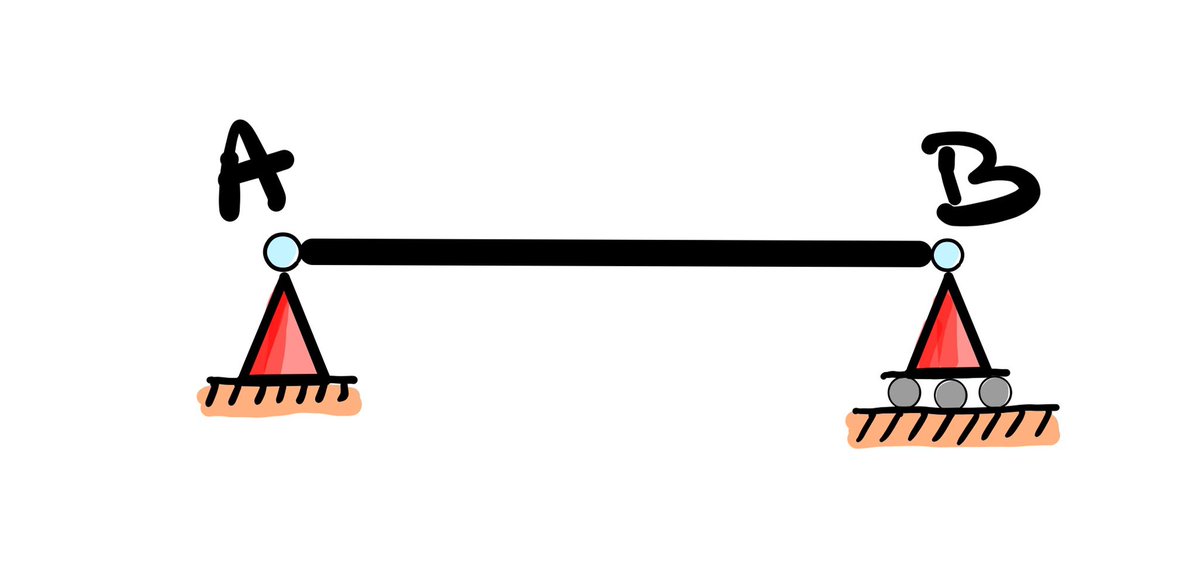
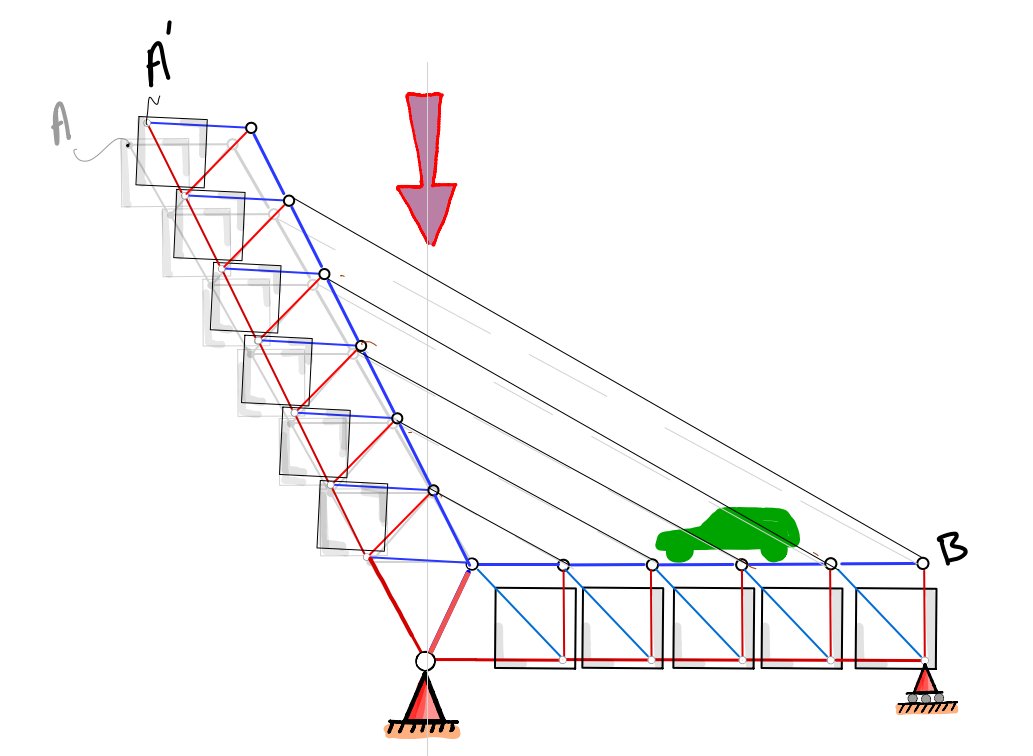
Los cables, al sentir la presencia cercana del vehículo, tiran del mástil, el cual se mueve hacia adentro (pasamos de A a A´). Para reducir este efecto, que hace que los cables pierdan tensión, se necesita que el pilono sea muy rígido (por eso es tan "gordo").
Una peculiaridad es que en el Alamillo los cables se pretensan hasta conseguir minimizar la flexión en el mástil. Esto es, que la fuerza en el elemento BC del sketch sea casi nula bajo cargas permanentes. Los cables tienen así una tensión "garantizada" bajo carga permanente.
Aún así, al hacerse los cables algo más cortos bajo cargas vivas (A´B<AB), los cables se aflojan, pierden tensión y pueden ser susceptibles de vibrar.
Un puente atirantado clásico tendría unos cables traseros o de retenida que harían el sistema más rígido. En la imagen se muestran algunas opciones clásicas.
..pero es que el puente del Alamillo no es un puente atirantado clásico. Eso lo hace especial y lleno, no sin razón, de controversia y polémica.
En cualquier caso, espero que os haya gustado el hilo! :-)
En cualquier caso, espero que os haya gustado el hilo! :-)
• • •
Missing some Tweet in this thread? You can try to
force a refresh
