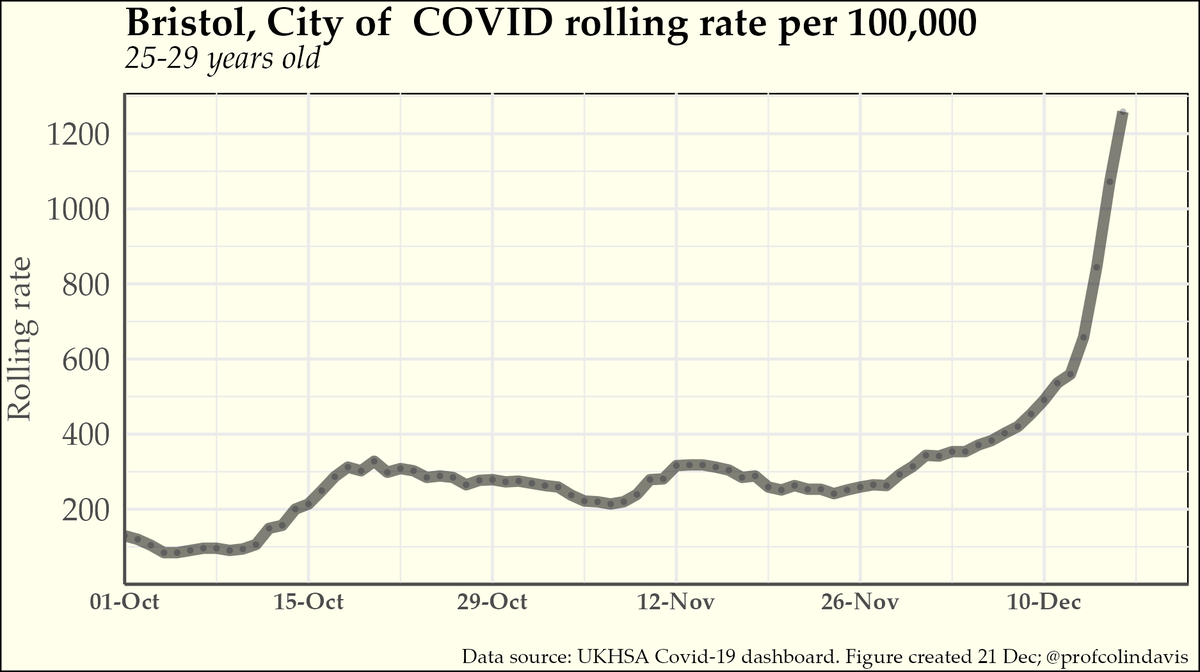
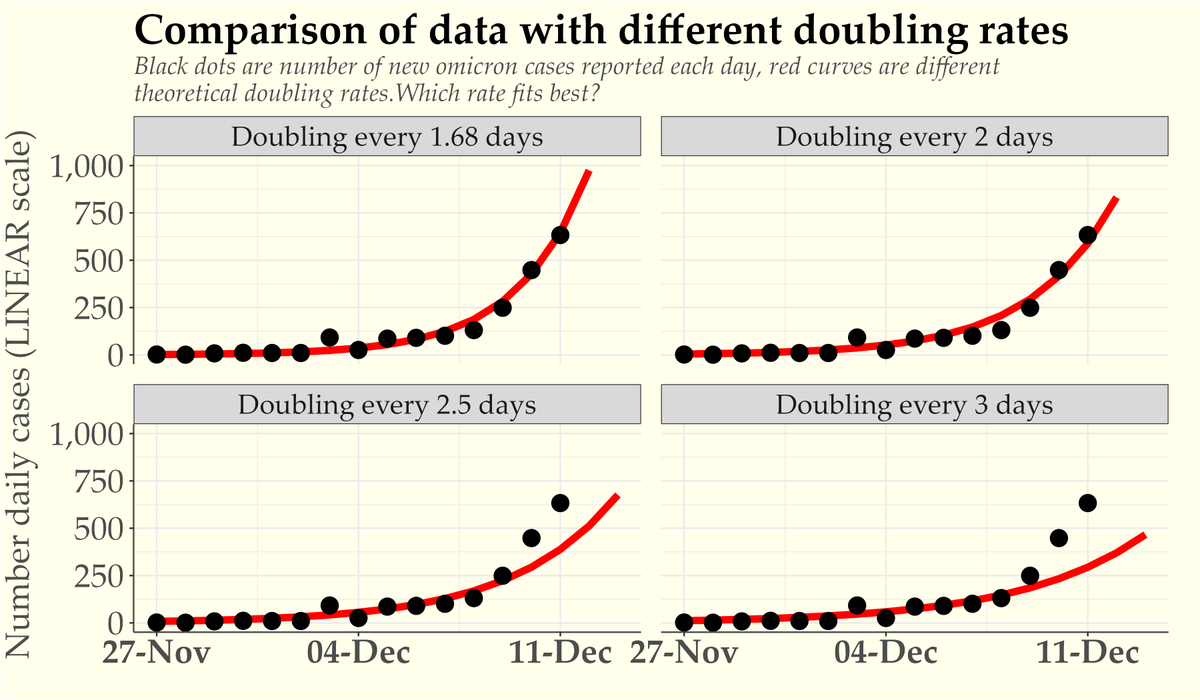
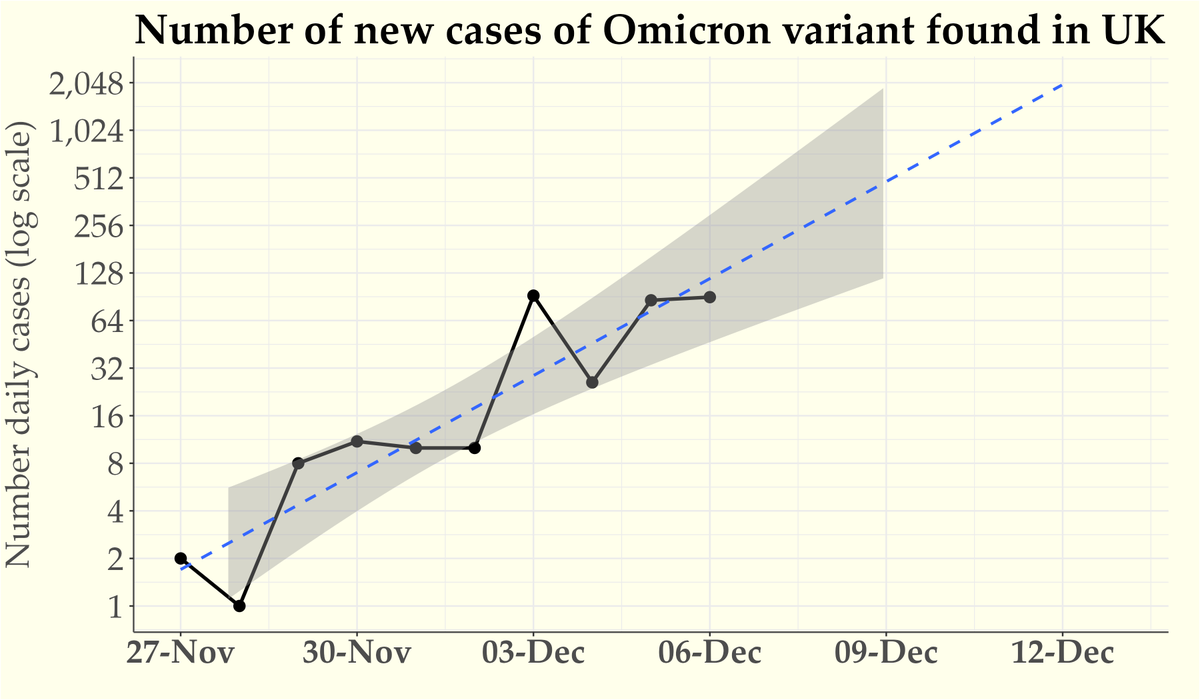
England Covid case data are grouped into about twenty 5-year age bands. For anyone who’s been paying attention it’ll come as no surprise that the first age group to have recorded more than 1 million cases (on Xmas Eve) is 10-14 year olds. Merry Christmas, kids. 🧵 

The red line on the graph shows how you’d expect the (roughly) 10 million cases so far in England to be distributed based on population statistics (the size of each age group). As you can see, some groups are over-represented in the cases and others are under-represented. 
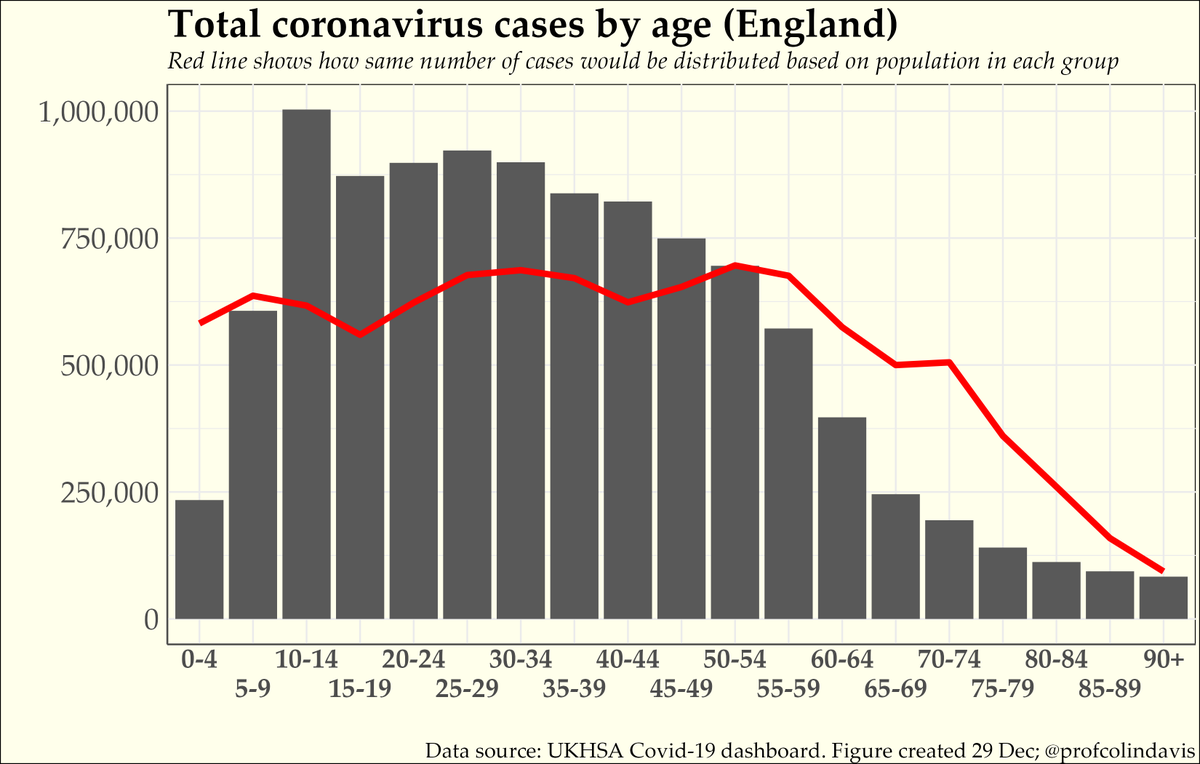
It’s not surprising that adults of working age are over-represented in the cases, whereas older adults (for whom it is easier to limit contacts) are under-represented. But the over-representation is greatest of all for school-age children.
Indeed, just the “overshoot” in cases from what would be expected for 10-19 year olds is considerably greater than the *total* number of cases recorded in all 70+ year olds.
It's reasonable to attribute some of the overshoot in cases among school-age children to higher levels of testing. But one can't get away from the fact that we have failed to provide children with a Covid-safe environment.
One indicator of which aspect of childrens' environment isn't Covid-safe is the way in which we see cases go up and down at regular intervals that just happen to coincide with term dates. School-age children have the highest rate of Covid cases because schools are not Covid-safe. 

Time and again the Dept for Education have failed to introduce mitigations (like ventilation and filtration) that would make schools safer. At the same time they've taken away mitigations like masks and bubbles that help to curb transmission.
And we're about to do it all again, but this time, apparently, without tests. This isn't safeguarding children's education -- it's the opposite. It's also endangering the health of children, their teachers and their families. 

With new records for hospitalisation of children being broken every day, the government's pretense that schools are Covid-safe is looking more and more reckless.
https://twitter.com/Antonio_Caramia/status/1476254428562960388?s=20
• • •
Missing some Tweet in this thread? You can try to
force a refresh