#超算数 谷村省吾さんは遠山啓さんの言葉を孫引きしていますが、実際には遠山さんは彼自身による「量の理論」に基き、かけ算順序固定強制指導を正当化する酷い発言も残しています。
添付画像②を参照。
「量の理論」がその後の算数教育に与えた悪影響について谷村さんは知っているでしょうか?続く

添付画像②を参照。
「量の理論」がその後の算数教育に与えた悪影響について谷村さんは知っているでしょうか?続く
https://twitter.com/tani6s/status/1479467600736583684
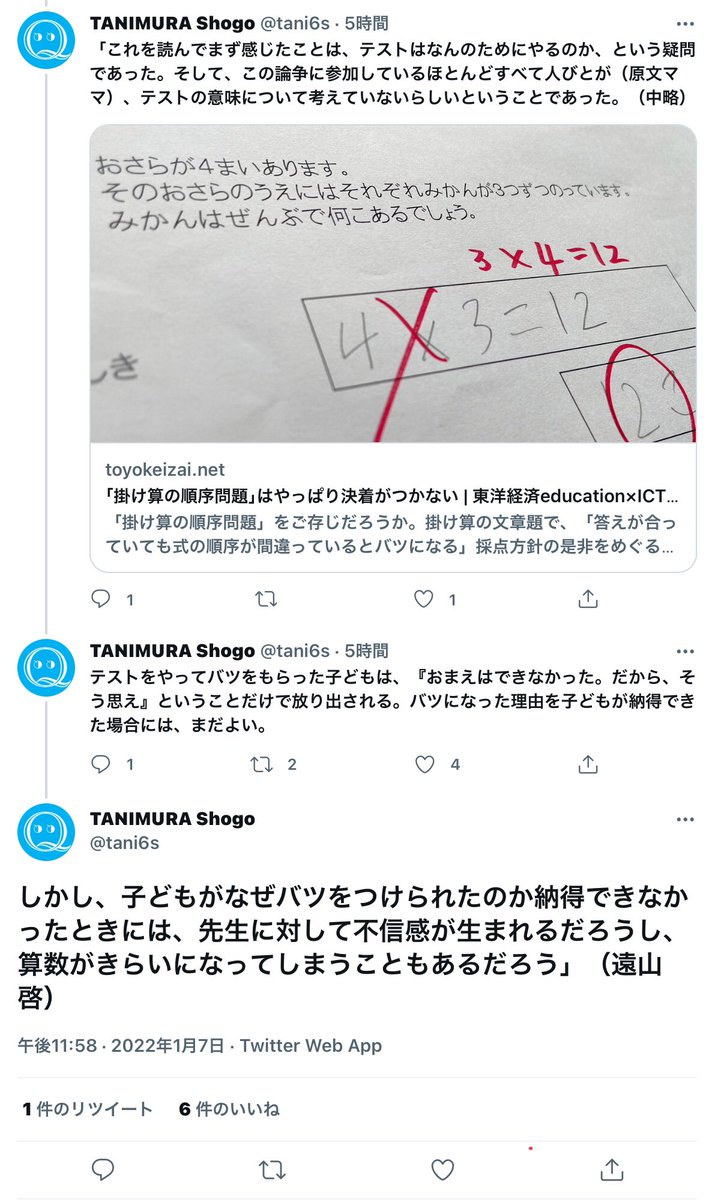

#超算数 遠山啓氏は、自身が広めた「内包量」という困りものの算数数学教育用語を用いてこう言った。
【乗法の交換法則が連続量にはまだ適用しないほうがよいとしたら〜外延量×内包量とは書かないほうがよいだろう】
【単価×分量~とは書くが~分量×単価〜とは書かない】
books.google.co.jp/books?id=Zaiaq…
【乗法の交換法則が連続量にはまだ適用しないほうがよいとしたら〜外延量×内包量とは書かないほうがよいだろう】
【単価×分量~とは書くが~分量×単価〜とは書かない】
books.google.co.jp/books?id=Zaiaq…

#超算数 「量の理論」についても教わってしまったのはまずかったと思います。
昔から数学関係者の一部には、遠山啓さんやその「量の理論」に好意的なせいで、遠山啓さん及びその弟子筋(特に銀林浩氏)が算数数学教育に与えた悪影響を無視する傾向があるという問題があります。
これは頭の痛い問題。
昔から数学関係者の一部には、遠山啓さんやその「量の理論」に好意的なせいで、遠山啓さん及びその弟子筋(特に銀林浩氏)が算数数学教育に与えた悪影響を無視する傾向があるという問題があります。
これは頭の痛い問題。
https://twitter.com/tani6s/status/1162570498489737216

#超算数 「内包量」は遠山啓さんが広めた用語であり、遠山さんはそのことを自慢しています。実際、遠山啓用語として「内包量」は最も有名なものだと言って良いでしょう。
そういう用語を用いて、かけ算順序固定強制指導の正当化に使えるおかしな発言をしているわけです。
印象が酷く悪い。
そういう用語を用いて、かけ算順序固定強制指導の正当化に使えるおかしな発言をしているわけです。
印象が酷く悪い。
https://twitter.com/genkuroki/status/1479555326781587456
#超算数 H. Weyl, Space, Time, Matter (1922) p.108には、「外延量」の元になったquantityと「内包量」の元になったintensityの説明があります。
この辺は現代的には多様体論をマスターしていれば易しい話題ですが、ほとんどの人にとっては理解不能な話題になっています。
archive.org/details/spacet…
この辺は現代的には多様体論をマスターしていれば易しい話題ですが、ほとんどの人にとっては理解不能な話題になっています。
archive.org/details/spacet…

#超算数 「外延量」の元になったらしいquantityは多様体上のテンソル場を意味し、「内包量」の元になったintensityは多様体上のテンソル密度場を意味しているようです。
警告:テンソル場やテンソル密度場は普通のまともな数学の話題だが、「外延量」「内包量」は杜撰な考え方になっているので注意!
警告:テンソル場やテンソル密度場は普通のまともな数学の話題だが、「外延量」「内包量」は杜撰な考え方になっているので注意!

#数楽 テンソル場の最も易しい場合はスカラー場です。
スカラー場は数学的には多様体上のスカラー値函数と同じ意味です。
スカラー密度場は多様体上のスカラー値測度と同じ意味です。局所座標系上では、f(x_1,…,x_n) |dx_1⋀…⋀dx_n| と書いておくと便利です。ここで| |は絶対値の意味です。
スカラー場は数学的には多様体上のスカラー値函数と同じ意味です。
スカラー密度場は多様体上のスカラー値測度と同じ意味です。局所座標系上では、f(x_1,…,x_n) |dx_1⋀…⋀dx_n| と書いておくと便利です。ここで| |は絶対値の意味です。
#超算数 H. Weylさんによるquantityとintensityの説明を読んだ人は誰でも「こんなに難しいことを、算数教育に直接関わっている人達の大部分は理解できるはずがない」と感じると思います。
実際、遠山啓さん用語の「外延量」「内包量」はWeylさんのquantity, intensityとは全然別の意味になっている。
実際、遠山啓さん用語の「外延量」「内包量」はWeylさんのquantity, intensityとは全然別の意味になっている。
#超算数 遠山啓的「外延量」の典型例は「質量」で、遠山啓的「内包量」の典型例は「質量の密度」です。
質量の密度はスカラー値測度でWeylさんの用語でのintensityの特別な場合になりますが、質量はスカラー場ではないのでquantityの特別な場合にはなりません。
質量の密度はスカラー値測度でWeylさんの用語でのintensityの特別な場合になりますが、質量はスカラー場ではないのでquantityの特別な場合にはなりません。
#超算数 「外延量」の定義は「加法性が成立している量」で熱力学的な示量変数に似ています。しかし、熱力学の文脈から外れているので、定義の内容はクリアではありません。
「内包量」の定義は「加法性が成立していない量」です。
もはやH. Weylさんのquantity, intensityとは完全に無関係!
「内包量」の定義は「加法性が成立していない量」です。
もはやH. Weylさんのquantity, intensityとは完全に無関係!
#超算数 遠山啓さんは、自分を信奉する算数教育関係者達の大部分が絶対に理解できそうもない文献を挙げて、自慢の「外延量」「内包量」という独自用語を権威付けしているわけです。
しかし、実際に普及させた「外延量」「内包量」の意味は権威付けに使った文献とは無関係になっている。
しかし、実際に普及させた「外延量」「内包量」の意味は権威付けに使った文献とは無関係になっている。

#超算数 遠山啓さんのこういうやり方は、数学関係者達が「算数は本当は難しい」のように言い出すことの原因になったと思う。
本当はシンプルで易しい算数の内容について、権威的で難解に見える理屈を述べ、その理屈に従って算数を教えるべきだとする傾向に、遠山啓さんは御墨付きを与えてしまった。
本当はシンプルで易しい算数の内容について、権威的で難解に見える理屈を述べ、その理屈に従って算数を教えるべきだとする傾向に、遠山啓さんは御墨付きを与えてしまった。
#超算数 そういう遠山啓さんが、
【外延量×内包量とは書かない方がよいだろう】(分量は外延量、単価は内包量)
【単価×分量~とは書くが~分量×単価~とは書かないし,それはひどく考えにくいだろう】
と書いていたことを、好意的に見逃すのは非常にまずいと私は思います。
books.google.co.jp/books?id=Zaiaq…
【外延量×内包量とは書かない方がよいだろう】(分量は外延量、単価は内包量)
【単価×分量~とは書くが~分量×単価~とは書かないし,それはひどく考えにくいだろう】
と書いていたことを、好意的に見逃すのは非常にまずいと私は思います。
books.google.co.jp/books?id=Zaiaq…

#超算数 レシートにも、国税庁のウェブサイトにも、「分量×単価」の順序で書かれたかけ算の式は普通に出て来ます。
そういう社会常識に反することを、遠山啓さんは自身の「量の理論」用語を使って述べているわけです。
添付画像②は nta.go.jp/law/joho-zeika… より

そういう社会常識に反することを、遠山啓さんは自身の「量の理論」用語を使って述べているわけです。
添付画像②は nta.go.jp/law/joho-zeika… より


#超算数 このスレッドを読めば、算数教育への悪影響を無視して、遠山啓さんや「量の理論」を安易にかつ好意的に引用してしまう人たちには問題があることは明らかだと私は思います。
危険物は危険物として慎重に取り扱うべきです。
遠山啓氏の「権威」に負けると色々おかしなことになる。
危険物は危険物として慎重に取り扱うべきです。
遠山啓氏の「権威」に負けると色々おかしなことになる。
#超算数 遠山啓氏の「高弟」の銀林浩氏曰く
【意味の上からは確かに
4+3≠3+4
であって厳密には交換法則は成り立たない】
【質量と力を掛けた運動量の方が外延的で,保存則が成り立つ】
注意:運動量は質量と速度の積。速度は内包量なので、運動量の正しい定義は不都合だったらしい。😅


【意味の上からは確かに
4+3≠3+4
であって厳密には交換法則は成り立たない】
【質量と力を掛けた運動量の方が外延的で,保存則が成り立つ】
注意:運動量は質量と速度の積。速度は内包量なので、運動量の正しい定義は不都合だったらしい。😅



#超算数 銀林浩氏は、より外延的だと言うために運動量の定義を質量と力に積に変更しているだけではなく、遠山啓氏が提案し、銀林氏が整備した「量の理論」の「外延量」と「内包量」をユングの意味の「外向的」「内向的」と結び付けている。
あの悪しき「現代思想」もテイストまで出している!😱
あの悪しき「現代思想」もテイストまで出している!😱

#超算数 「量の理論」について「まじめ」に勉強しようとすると、このような銀林浩氏の著書や解説を読むことになってしまいます。なぜならば「量の理論」を整備したのはこの銀林浩氏だからです。
ここまで説明しても「量の理論」が危険物だと分からない数学者や物理学者は皆無だと思いたいです。
ここまで説明しても「量の理論」が危険物だと分からない数学者や物理学者は皆無だと思いたいです。
#超算数 「量の理論」について、どのように解説がされているかについては、積分定数さんがよく調べているので参考になります。
次のリンク先で閲覧できます。
↓
twilog.org/sekibunnteisuu…
例えば
↓
次のリンク先で閲覧できます。
↓
twilog.org/sekibunnteisuu…
例えば
↓
https://twitter.com/sekibunnteisuu/status/992600274618408960
#超算数 訂正
❌あの悪しき「現代思想」もテイストまで出している!😱
⭕️あの悪しき「現代思想」のテイストまで出している!😱
本当はシンプルで易しい算数について、権威的で曖昧で晦渋な「理論」を作り、それに基いて算数を教えようとする態度は、最終的に悪しき「現代思想」に達してしまった。
❌あの悪しき「現代思想」もテイストまで出している!😱
⭕️あの悪しき「現代思想」のテイストまで出している!😱
本当はシンプルで易しい算数について、権威的で曖昧で晦渋な「理論」を作り、それに基いて算数を教えようとする態度は、最終的に悪しき「現代思想」に達してしまった。
#数楽 n-form dx_1⋀…⋀dx_nと測度 |dx_1⋀…⋀dx_n| の区別については以下のリンク先スレッドを参照。
その区別は本質的にGL_n(ℝ)の1次元表現としての違いの話になっています。
ℝ上の1-form dx とLebesgue測度 |dx| の区別の場合が最も易しい場合です。
その区別は本質的にGL_n(ℝ)の1次元表現としての違いの話になっています。
ℝ上の1-form dx とLebesgue測度 |dx| の区別の場合が最も易しい場合です。
https://twitter.com/genkuroki/status/1354635247267188744
#数楽 f(x) dx 全体の次元(「単位」の意味での次元)がUで、dxが長さの次元Lを持つとき、f(x)の次元はU/Lになります。
同様に、g(x)|dx| 全体の次元がUのとき、g(x)の次元はU/Lになる。
しかし、1-form f(x) dxと測度 g(x) |dx| は異なります。
その辺の区別は単なる次元解析では不可能。
同様に、g(x)|dx| 全体の次元がUのとき、g(x)の次元はU/Lになる。
しかし、1-form f(x) dxと測度 g(x) |dx| は異なります。
その辺の区別は単なる次元解析では不可能。
#数楽 H. Weyl 『空間・時間・物質』は現代的には多様体論の言葉で次元解析では不可能な区別も可能な定式化の方法について説明している有名な本だとみなせます。
だから、次元解析の発展形について語っている人が、H. Weyl 『空間・時間・物質』を引用していない場合は色々要注意だと思います。
だから、次元解析の発展形について語っている人が、H. Weyl 『空間・時間・物質』を引用していない場合は色々要注意だと思います。
#数楽 多様体は座標系を貼り合わせたものとみなせ、多様体上の場は異なる座標系上での値の貼り合わせ方によって定義されます。
場の貼り合わせのルールが座標変換のJacobi行列の線形表現で書けている場合には、本質的にGl_n(ℝ)の表現によって貼り合わせのルールが決められていることになります。続く
場の貼り合わせのルールが座標変換のJacobi行列の線形表現で書けている場合には、本質的にGl_n(ℝ)の表現によって貼り合わせのルールが決められていることになります。続く
#数楽 例えば2次元の多様体の場合に、座標系(x,y)における2-form dx⋀dy と座標系(u,v)における2-form du⋀dv はJacobi行列
J =
[ ∂x/∂u ∂x/∂v ]
[ ∂y/∂u ∂xy/∂v ]
の行列式倍で貼り合わさっている:
dx⋀dy = det(J) du⋀dv.
det : GL_2(ℝ) → GL_1(ℝ)はGL_2(ℝ)の1次元表現。
J =
[ ∂x/∂u ∂x/∂v ]
[ ∂y/∂u ∂xy/∂v ]
の行列式倍で貼り合わさっている:
dx⋀dy = det(J) du⋀dv.
det : GL_2(ℝ) → GL_1(ℝ)はGL_2(ℝ)の1次元表現。
#数楽 座標系(x,y)におけるLebesgue測度|dx⋀dy|と座標系(u,v)におけるLebesgue測度|du⋀dv|は、Jacobi行列の行列式の絶対値倍で貼り合わさっている:
|dx⋀dy| = abs(det(J)) |du⋀dv|.
abs⚪︎det : GL_2(ℝ) → GL_1(ℝ) は det とは異なるGL_2(ℝ)の1次元表現になっています。
|dx⋀dy| = abs(det(J)) |du⋀dv|.
abs⚪︎det : GL_2(ℝ) → GL_1(ℝ) は det とは異なるGL_2(ℝ)の1次元表現になっています。
#数楽 もっと一般のややこしい場合も同様に GL_n(ℝ) の表現の違いとして区別が可能になります。
実際には、貼り合わせは線形とは限らないことへの注意も必要です。例えば、接続(connection)。接続はゲージ理論の主対象でもあります。
実際には、貼り合わせは線形とは限らないことへの注意も必要です。例えば、接続(connection)。接続はゲージ理論の主対象でもあります。
#数楽 しかし、Weylさんの本の異なる座標系上の値の貼り合わせで全部理解できます。(もちろん最初から座標不変な定式化も可能。)
この辺はずっと前から数学的によく整備されているところです。
単純な次元解析だけで区別できないものを区別したければ、昔からある数学を勉強してくださいと言いたい。
この辺はずっと前から数学的によく整備されているところです。
単純な次元解析だけで区別できないものを区別したければ、昔からある数学を勉強してくださいと言いたい。
#超算数 「量の理論」のような危険物に触れなくても、遠山啓さんが権威付けのために持ち出したWeylさんの有名な本がとても良い本で、Weylさんの本やその後の多様体及びその上の各種の場の定式化の整理に従えば、単純な次元解析を超えることが既存の数学で普通にできるという仕組みになっています。
#数楽 自明な訂正
❌J =
[ ∂x/∂u ∂x/∂v ]
[ ∂y/∂u ∂xy/∂v ]
⭕️J =
[ ∂x/∂u ∂x/∂v ]
[ ∂y/∂u ∂y/∂v ]
この手の誤植はどうしてもなくならない。
❌J =
[ ∂x/∂u ∂x/∂v ]
[ ∂y/∂u ∂xy/∂v ]
⭕️J =
[ ∂x/∂u ∂x/∂v ]
[ ∂y/∂u ∂y/∂v ]
この手の誤植はどうしてもなくならない。
https://twitter.com/genkuroki/status/1479605288621985792
#超算数 引用
【量の計算を見直す
このスキャン・ファイルは谷村省吾教授(~)から送って頂いた。心から感謝する。】
私は、遠山啓さんよりずっと前からあるWeylさんの本やその後整備された多様体上の場の定式化を参照しておかないと、おかしなことになると思う。
math.oshirase.com/%E9%87%8F%E3%8…
【量の計算を見直す
このスキャン・ファイルは谷村省吾教授(~)から送って頂いた。心から感謝する。】
私は、遠山啓さんよりずっと前からあるWeylさんの本やその後整備された多様体上の場の定式化を参照しておかないと、おかしなことになると思う。
math.oshirase.com/%E9%87%8F%E3%8…

#超算数 谷村省吾さんがスキャンファイルを送ってくれて心から感謝している小島順さんがかけ算順序固定強制指導問題にどのようにコメントしているかについては、以下のリンク先スレッドを参照。
本当に頭痛がして来そうな話題だと思います。
本当に頭痛がして来そうな話題だと思います。
https://twitter.com/ookubotact/status/1273532250353618947
#超算数 子供の親にとって、算数教育の伝統が支えている有害な教え方はものすごくリアルな問題です。
遠山啓氏の「量の理論」の数学関係者や物理関係者への普及は、その問題の解決に数学者や物理学者の力を利用しようとするときの主要な障碍になっているのです。
本当に頭の痛い問題だと思います。
遠山啓氏の「量の理論」の数学関係者や物理関係者への普及は、その問題の解決に数学者や物理学者の力を利用しようとするときの主要な障碍になっているのです。
本当に頭の痛い問題だと思います。
#超算数 誤解しないように注意:かけ算順序固定強制指導には、遠山啓さんの「量の理論」用語を使ったバージョンよりもずっと前からあります。100年以上の歴史がある。
https://twitter.com/genkuroki/status/1479619181868105729
#数楽 n=2の場合の座標変換のJacobi行列式を
J =
[ ∂x/∂u ∂x/∂v ]
[ ∂y/∂u ∂y/∂v ]
書くときの2-formの変換則
dx⋀dy = det(J) du⋀dv
と測度の変換則
|dx⋀dy| = abs(det(J))|du⋀dv|
の違いの話は既出のWeylさんの本に書いてあるとみなせます。添付画像のページには後者の説明がある。
J =
[ ∂x/∂u ∂x/∂v ]
[ ∂y/∂u ∂y/∂v ]
書くときの2-formの変換則
dx⋀dy = det(J) du⋀dv
と測度の変換則
|dx⋀dy| = abs(det(J))|du⋀dv|
の違いの話は既出のWeylさんの本に書いてあるとみなせます。添付画像のページには後者の説明がある。

#数楽 2-form f(x,y)dx⋀dyを積分するときに「向き」が必要になりますが、測度 g(x,y)|dx⋀dy|であれば「向き」無しで積分できます。
Weylさんの本では密度場の定義として後者の測度の方を採用しているわけです。
しつこいですが、Weylさんの本の1922年の英語版に書いてある。
Weylさんの本では密度場の定義として後者の測度の方を採用しているわけです。
しつこいですが、Weylさんの本の1922年の英語版に書いてある。
#数楽 Weylさんの本の英語版は1922年の本なので、その後の抽象的一般論をきれいに展開する技術は取り入れられていないのですが、その部分は現代の数学科では多様体論として普通に教えられている内容なので、答えを知っていれば大した話ではないです。
#数楽 dx⋀dy と |dx⋀dy| の違いは det(J) と abs(det(J)) の違い
abs(det(J))/det(J) = sign(det(J)) = ±1
で、
|dx⋀dy|/(dx⋀dy) = sign(det(J)) |du⋀dv|/(du⋀dv)
によって、|dx⋀dy|/(dx⋀dy)の変換則も自然に定まります。
こういうことも「特別な何か」抜きに易しく理解できます。
abs(det(J))/det(J) = sign(det(J)) = ±1
で、
|dx⋀dy|/(dx⋀dy) = sign(det(J)) |du⋀dv|/(du⋀dv)
によって、|dx⋀dy|/(dx⋀dy)の変換則も自然に定まります。
こういうことも「特別な何か」抜きに易しく理解できます。
#数楽 以上のようなWeylさんの本(英語版は1922年)の密度場(測度)の定式化は言うまでもなく、遠山啓さんの「量の理論」やその影響を受けた小島順さんよりも数十年間先行しているわけです。
ところが、以上のクリアな話が小島順さんの1977年の説明を見ると、微妙にクリアでなくなってしまうのです。
ところが、以上のクリアな話が小島順さんの1977年の説明を見ると、微妙にクリアでなくなってしまうのです。
#数楽 添付画像は
math.oshirase.com/%E9%87%8F%E3%8…
↓
math.oshirase.com/wp-content/upl…
5. 量の分類
小島順「数学セミナー」誌連載 1977年12月号
より。
そこでは、2つの向きからなる2点集合 Or X⃗ を経由して、同値関係で割るという汚い処理をしてある。続く

math.oshirase.com/%E9%87%8F%E3%8…
↓
math.oshirase.com/wp-content/upl…
5. 量の分類
小島順「数学セミナー」誌連載 1977年12月号
より。
そこでは、2つの向きからなる2点集合 Or X⃗ を経由して、同値関係で割るという汚い処理をしてある。続く


#数楽 以上で紹介したWeylさんの定式化の書き直しの場合では、Or X⃗を使っている部分は
|dx⋀dy|/(dx⋀dy) を使った部分に対応しています。
そして、その変換則がsign(det(J))=±1倍になることが、Or X⃗が2点集合になることに対応していると思える。
|dx⋀dy|/(dx⋀dy) を使った部分に対応しています。
そして、その変換則がsign(det(J))=±1倍になることが、Or X⃗が2点集合になることに対応していると思える。
#数楽 2-form dx⋀dy に |dx⋀dy|/(dx⋀dy) をかけると、測度 |dx⋀dy| になるという話は、小島順さんのやり方だと、2点集合 Or X⃗ との直積を同値関係で割る話になってしまっています。
Weylさん的説明と小島順さんの説明のどちらが分かりやすいと思いますか?
Weylさんの方が分かりやすくないか?
Weylさん的説明と小島順さんの説明のどちらが分かりやすいと思いますか?
Weylさんの方が分かりやすくないか?
#数楽 Weylさん的定式化では、微分形式 dx⋀dy と |dx⋀dy|/(dx⋀dy) をかけると測度 |dx⋀dy| が得られる話を、GL_2(ℝ)の表現の普通の意味でのテンソル積(⊗)で理解できます。
小島順さんのやり方だとそうなっておらず、内容的にクリアでなくなってしまっている。
小島順さんのやり方だとそうなっておらず、内容的にクリアでなくなってしまっている。
#数楽 で、ググると2012年の文書だと思うのですが、谷村省吾さんは、遠山啓さんも参考にしたと言っているWeylさんの本に戻らず、なぜか小島順さんの数セミの記事を勉強してしまっていることがわかります。
sceng.kochi-tech.ac.jp/koban/quatuo/l…
sceng.kochi-tech.ac.jp/koban/quatuo/l…

#数楽 小島順さんの定式化はクリアでないと私は思うのですが、銀林浩さんと違って普通に数学の話になっているので、小島順さんの記事を引用することには問題ない。
しかし、銀林浩氏が書いたものまで安易に引用するのは個人的に非常にまずいと思っています。
sceng.kochi-tech.ac.jp/koban/quatuo/l…
しかし、銀林浩氏が書いたものまで安易に引用するのは個人的に非常にまずいと思っています。
sceng.kochi-tech.ac.jp/koban/quatuo/l…

#数楽 添付画像は
sceng.kochi-tech.ac.jp/koban/quatuo/l…
2015 年1月11-12日
第4回QUATUO研究会
電磁気の幾何学と単位系
谷村省吾
より。
小島順さんに従ったせいで、O(V)が2点集合になり、「O(V)⊗」の定義の説明が別に必要になっている(説明はない)。
クリアでなくなる定式化の採用はやはり苦しい。
sceng.kochi-tech.ac.jp/koban/quatuo/l…
2015 年1月11-12日
第4回QUATUO研究会
電磁気の幾何学と単位系
谷村省吾
より。
小島順さんに従ったせいで、O(V)が2点集合になり、「O(V)⊗」の定義の説明が別に必要になっている(説明はない)。
クリアでなくなる定式化の採用はやはり苦しい。

#超算数 「量の理論」の周囲には大量の地雷が埋まっているので、危険物扱いしないと、色々な意味でまずいことになる可能性が高いです。
Weylさんのような鉄板で信頼できる数学者が書いた数学書を参考にすることは非常に安全。ただし、Weylさんが書いた本は結構難しいことが多い。
Weylさんのような鉄板で信頼できる数学者が書いた数学書を参考にすることは非常に安全。ただし、Weylさんが書いた本は結構難しいことが多い。
#数楽
en.wikipedia.org/wiki/Density_o…
Density on a manifold - Wikipedia
でも、2点集合にせずに、GL_n(V)の1次元表現として、向き Or(V) を定義していますね。”Or(V)⊗" を別に定義する必要がない。
あとモチベーションも平行2n面体の体積として自然に説明されている。
en.wikipedia.org/wiki/Density_o…
Density on a manifold - Wikipedia
でも、2点集合にせずに、GL_n(V)の1次元表現として、向き Or(V) を定義していますね。”Or(V)⊗" を別に定義する必要がない。
あとモチベーションも平行2n面体の体積として自然に説明されている。

#数楽
nlab-pages.s3.us-east-2.amazonaws.com/nlab/show/inte…
nLab
integration of differential forms
にはp-pseudoform (捩形式と同じもの)の場合についても書いてあります。実質「向き」について考え直すだけの話。
nlab-pages.s3.us-east-2.amazonaws.com/nlab/show/inte…
nLab
integration of differential forms
にはp-pseudoform (捩形式と同じもの)の場合についても書いてあります。実質「向き」について考え直すだけの話。
• • •
Missing some Tweet in this thread? You can try to
force a refresh