Se impone, de nuevo, la necesidad de aclarar algunos conceptos básicos para saber “leer” la actualidad.
Hablemos de tasas de crecimiento interanual.
Hablemos de tasas de crecimiento interanual.
Para medir la evolución de las series económicas (y no economicas) en el tiempo usamos algunas transformaciones (en el argot “coyuntero” lo llamamos filtros).
La más sencilla es la tasa de crecimiento.
La más sencilla es la tasa de crecimiento.
La fórmula es sencilla:
[X(0)-X(1)]/X(1)
Donde X es la serie que observamos y el numero entre paréntesis refleja el momento de tiempo (0 si es hoy y 1 un periodo anterior).
Esta variación se multiplica por 100 para obtener la tasa en %.
[X(0)-X(1)]/X(1)
Donde X es la serie que observamos y el numero entre paréntesis refleja el momento de tiempo (0 si es hoy y 1 un periodo anterior).
Esta variación se multiplica por 100 para obtener la tasa en %.
Si tenemos series de frecuencia mayor a la anual (mensual o trimestral, por ejemplo), dependiendo de qué valor pongamos en 1 tenemos una tasa Intermensual o intertrimestral (mes o trimestre anterior) y la famosa tasa interanual (mismo mes o trimestre de año anterior).
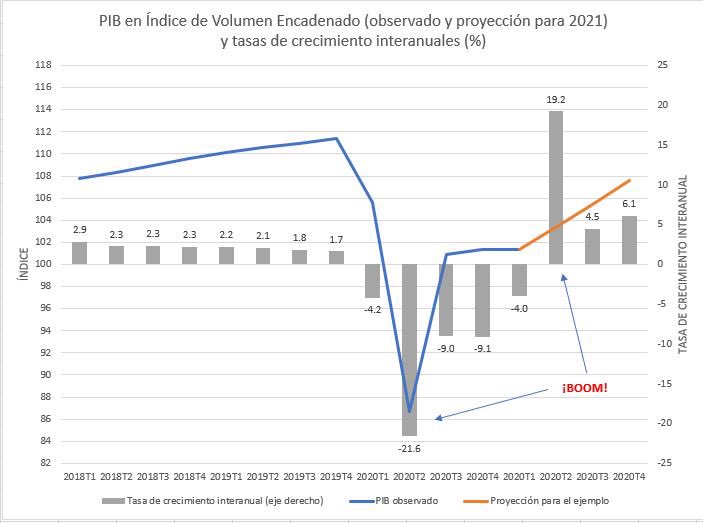
En general, la interanual es la más interesante. ¿Por qué? Porque por razones matemáticas es capaz de “filtrar”, aunque sea de forma imperfecta, la estacionalidad, componente de una serie temporal que debe ser eliminada si queremos percibir adecuadamente la evolución de la misma.
Sin embargo, hay un pequeño problema. La interanual es, en muy buena parte, una mirada al pasado, por lo que si tu objetivo es analizar la coyuntura, tienes un problema.
Simples mates nos lo enseña.
Simples mates nos lo enseña.
Sea T la tasa de crecimiento de la variable X, asumamos mensual, en términos interanuales. Es decir:
Y=[X(0)-X(11)]/X(11)
Donde 0 es este mes y 11 el mismo del año anterior.
Ahora hagamos un pequeño truco. Cojamos los meses intermedios entre esos dos y sumemos y restemos
Y=[X(0)-X(11)]/X(11)
Donde 0 es este mes y 11 el mismo del año anterior.
Ahora hagamos un pequeño truco. Cojamos los meses intermedios entre esos dos y sumemos y restemos
cada uno dentro de los corchetes.
Así,
Y=[{X(0)-X(1)}+{X(1)-X(2)}+…+{X(10)-X(11)}]/X(11)
Lo que tenemos es que la suma en el numerador es la suma de los crecimientos mensuales de la serie en tasas absolutas.
Con un poco de mates más tenemos
Así,
Y=[{X(0)-X(1)}+{X(1)-X(2)}+…+{X(10)-X(11)}]/X(11)
Lo que tenemos es que la suma en el numerador es la suma de los crecimientos mensuales de la serie en tasas absolutas.
Con un poco de mates más tenemos
Y={[X(0)-X(1)]/X(1)}*(X(1)/X(11)) +
{[X(1)-X(2)]/X(2)}*(X(2)/X(11)) +
{[X(2)-X(3)]/X(3)}*(X(3)/X(11)) +
….
+
{[X(10)-X(11)]/X(11)}*(X(10)/X(11))
{[X(1)-X(2)]/X(2)}*(X(2)/X(11)) +
{[X(2)-X(3)]/X(3)}*(X(3)/X(11)) +
….
+
{[X(10)-X(11)]/X(11)}*(X(10)/X(11))
Es decir, la tasa interanual es la media ponderada por el peso relativo del indicador en cada mes respecto al de aquel mes sobre el que comparamos de las diferentes tasas de crecimiento intermensuales.
Dicho en otras palabras, es la suma de doce términos de los cuales 11 ya son pasado y solo 1 es lo que ahora ocurre.
¿Y esto es para …?
Pues para entender bien la actualidad hay que saber qué medimos.
Si en un año la evolución de un indicador es muy estable, la tasa interanual es un estadístico interesante y de buenas propiedades ya que su valor no va a decir mucho más que la
Pues para entender bien la actualidad hay que saber qué medimos.
Si en un año la evolución de un indicador es muy estable, la tasa interanual es un estadístico interesante y de buenas propiedades ya que su valor no va a decir mucho más que la
evolución tendencial media de la serie en el ciclo que refleje. Si todos los meses anteriores al actual se comportaron de forma similar al último, la interanual es un buen indicador para saber qué está pasando.
Sin embargo, si dentro de un mismo año ha habido meses con comportamientos muy extravagantes o extremos, la interanual no tiene tanto sentido, ya que estará muy condicionado a esos valores extremos. Así, lo mejor es desestacionalizar series y mirar sus tasas intermensuales.
Obviamente, si queremos saber qué ha pasado en el año, puede interesarnos. Seguro. Pero si queremos ver las dinámicas más actuales, la interanual no es lo apropiado, pues es como mirar a las estrellas. Vemos el pasado y no el presente.
FIN
FIN
• • •
Missing some Tweet in this thread? You can try to
force a refresh