Thread by @EnDirectDuLabo

Vous l'attendiez, vous l'espériez : voici un thread sur les mathématiques du #ferroviaire 🚆
Et plus précisément, sur la notion de #graphe, qui est centrale dans ma recherche. C'est parti ⬇️ (1/N)

Un graphe, ce n'est rien qu'un ensemble de points et de lignes. Les points sont appelés "sommets", et les lignes qui relient ces sommets 2 à 2 sont des "arêtes".
Le plan de votre métro préféré est un bon exemple de graphe. (2/N)

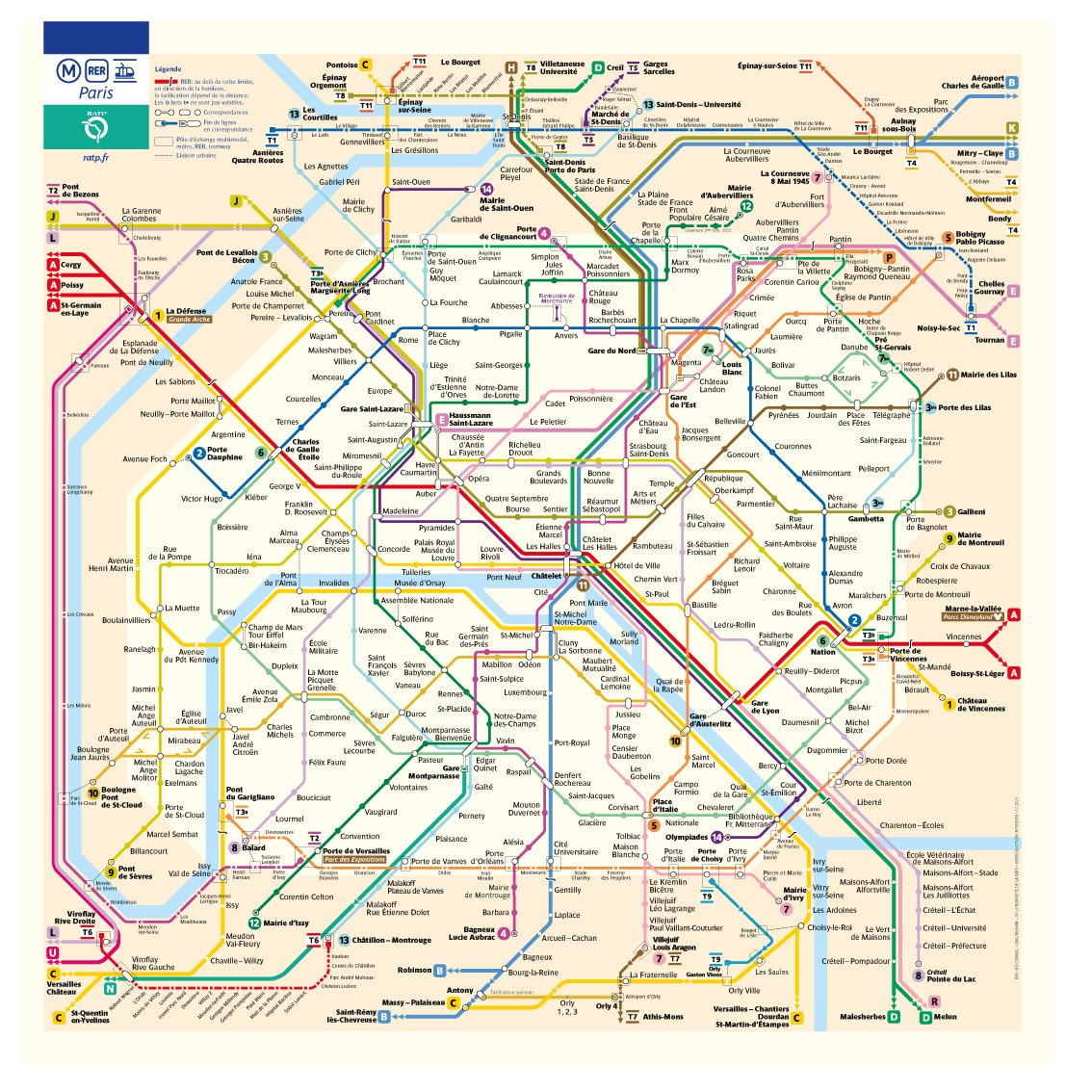
Quand ce métro fonctionne, on se demande souvent quel est le trajet le plus court entre deux stations. Parfois, ça se voit à l'oeil nu, et sinon on ouvre CityMapper.
Mais comment fonctionne CityMapper ? La réponse se trouve en 1956 à la terrasse d'un café d'Amsterdam... (3/N)

C'est là qu'E. Dijkstra invente, en 20 minutes et sans papier, l'algorithme qui le rendra célèbre. Il propose d'explorer le graphe par cercles concentriques, en partant du sommet initial et jusqu'à rencontrer la destination. (4/N)
en.wikipedia.org/wiki/Dijkstra%…

La durée de cette procédure est ~ proportionnelle au nombre d'arêtes de notre graphe. C'est une bonne nouvelle : même pour de grands réseaux comme le métro de Paris, on peut appliquer l'algorithme de Dijkstra en un temps raisonnable. (5/N)

La recherche d'itinéraires est donc un problème "facile". Passons maintenant à un autre exemple : l'affectation des trains aux quais dans une gare.
Quel rapport avec les graphes, me direz-vous ? À vos crayons, on va parler de coloriages 🖍️! (6/N)

Imaginez que chaque quai possède une couleur différente : affecter les quais aux trains, c'est donner à chaque train la couleur de son quai.
Mais attention, on ne colorie pas n'importe comment ! Deux trains qui arrivent en même temps ne peuvent pas avoir la même couleur... (7/N)

... sinon c'est la collision garantie ! Pour représenter ces incompatibilités, rien de tel qu'un graphe : les sommets correspondent aux trains, et les arêtes aux paires de trains qui ne peuvent pas utiliser le même quai. (8/N)

Dans ce graphe un peu abstrait, on veut choisir une couleur pour chaque sommet, de sorte que deux sommets adjacents (donc deux trains incompatibles) aient toujours des couleurs différentes. Si on arrive à faire ça, on aura une affectation sans collision 🥳 (9/N)

Malheureusement, on peut prouver qu'il n'existe pas d'algorithme polynomial pour colorier un graphe : ce problème est dit "NP-complet". Mais je ne suis pas au chômage pour autant, car on dispose de méthodes très efficaces en pratique ! (10/N)

L'astuce, c'est d'adapter nos méthodes au problème particulier que l'on veut résoudre. Par exemple, mon projet de recherche actuel vise à exploiter l'historique des instances rencontrées dans le passé, dans l'espoir d'améliorer la résolution dans l'avenir ! (11/N)

Si vous voulez en savoir plus sur ce domaine merveilleux appelé "recherche opérationnelle", voici deux excellents ouvrages de vulgarisation : (12/N)
press.princeton.edu/books/paperbac…
microlinkcolleges.net/elib/files/und…