Discover and read the best of Twitter Threads about #week10
Most recents (3)
Now that my #VisualAlgebra class is in the books, I want to post a long "meta thread" of all 16 weekly threads, with daily summaries. Here's my entire class, including lectures, HW, & exams, in one convenient place.
And stayed tuned for some surprise announcements below!šš§µ
And stayed tuned for some surprise announcements below!šš§µ
We started #Week1 of #VisualAlgebra with a few quotes from "A Mathematician's Apology" on the beauty of mathematics, and then saw Cayley diagrams for the symmetries of the rectangle and triangle.
In #Week2 of #VisualAlgebra, we explored the Rubik's cube, more Cayley diagrams, group presentations, the impossibility of the word & halting problems, and we classified all frieze groups.
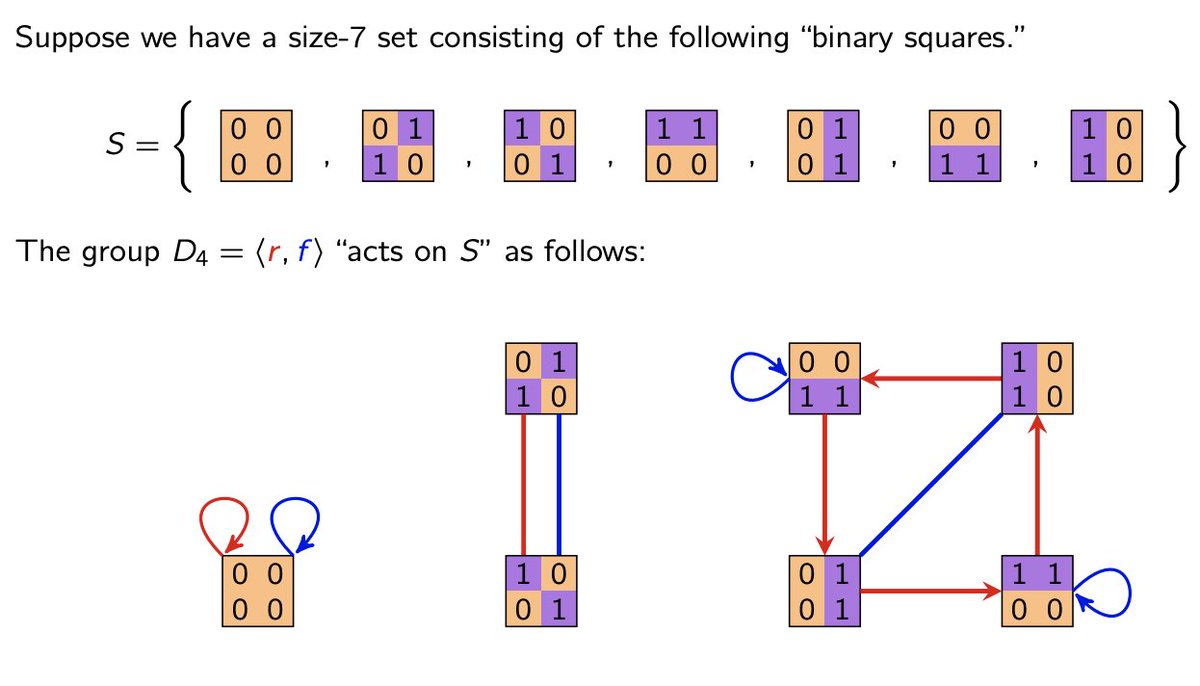
I woke up a few days ago with the sobering realization: actually, I do NOT really understand groups actions.
Spoiler: I do now, but it took some work. And now I realize how incomplete my understanding was. š³
Let me explain, I think some of you might enjoy this!
1/12 š§µš
Spoiler: I do now, but it took some work. And now I realize how incomplete my understanding was. š³
Let me explain, I think some of you might enjoy this!
1/12 š§µš
See those "orbit diagrams" above? I got to thinking: "how can we characterize all possible diagrams?" Equivalently, all transitive actions of D_4 (or a group G in general).
Playing around with things, I came up with a few more. But I still didn't know the answer. Do you?
2/12
Playing around with things, I came up with a few more. But I still didn't know the answer. Do you?
2/12
For example, how many of the following are possible?
Before reading on, see if you can answer this, and generalize to arbitrary groups.
There's a simple elegant answer, that I was never aware of. And I suspect that the majority of people who teach algebra aren't either.
3/12
Before reading on, see if you can answer this, and generalize to arbitrary groups.
There's a simple elegant answer, that I was never aware of. And I suspect that the majority of people who teach algebra aren't either.
3/12
We started #Week11 of #VisualAlgebra with a new diagram of one of the isomorphism theorems. I made this over spring break. The concept is due to Douglas Hofstadter (author of "Gƶdel, Escher, Bach"), who calls this a "pizza diagram".
1/14 Mon š§µš
1/14 Mon š§µš
Though we constructed semidirect products visually last week, we haven't yet seen the algebraic definition. On Friday, we saw inner automorphisms, which was the last step we needed.
Recall the analogy for AāB:
A = automorphism, B = "balloon".
2/14 M
Recall the analogy for AāB:
A = automorphism, B = "balloon".
2/14 M
Next, we asked when a group G is isomorphic to a direct product or semidirect product of its subgroups, N & H.
Here are two examples of groups that we are very familiar with.
3/14 M
Here are two examples of groups that we are very familiar with.
3/14 M
