Thread by @Pedrodanielpg

De vez en cuando los matemáticos alzamos la voz para decir que los sorteos por apellidos son INJUSTOS.

No es que los matemáticos nos quejemos siempre, pero lo hacemos en cuanto vemos algo injusto.

Pero, ¿cómo de injusto es esto?

Allá va un breve hilo con un caso real.

Supongamos que en una oposición quedan por asignarse 3 PLAZAS.

Por casualidades de la vida, 100 personas tienen exactamente la misma puntuación, han hecho los mismos cursos, y tienen todo el CV exactamente igual.

¿Cómo asignamos las plazas?
Pues vamos a tener que sortearlas...

Aquí abrimos un pequeño paréntesis porque para que este "caso práctico" sea lo más real posible, necesitamos una lista con los nombres y apellidos de 100 personas.

Claro, la ley de protección de datos dice que no puedo coger una lista y subirla aquí, así que hay que generar una.

Por suerte con los datos del INE podemos generar una lista que represente fielmente a la población española (ponderando apellidos y nombres).

Hay muchas herramientas que permiten hacer eso, yo he usado proinf.net/permalink/gene….

Mi lista de 100 nombres y apellidos es esta:

Como todos han sacado la misma nota, el orden de la lista da igual, así que las he ordenado alfabéticamente por comodidad.

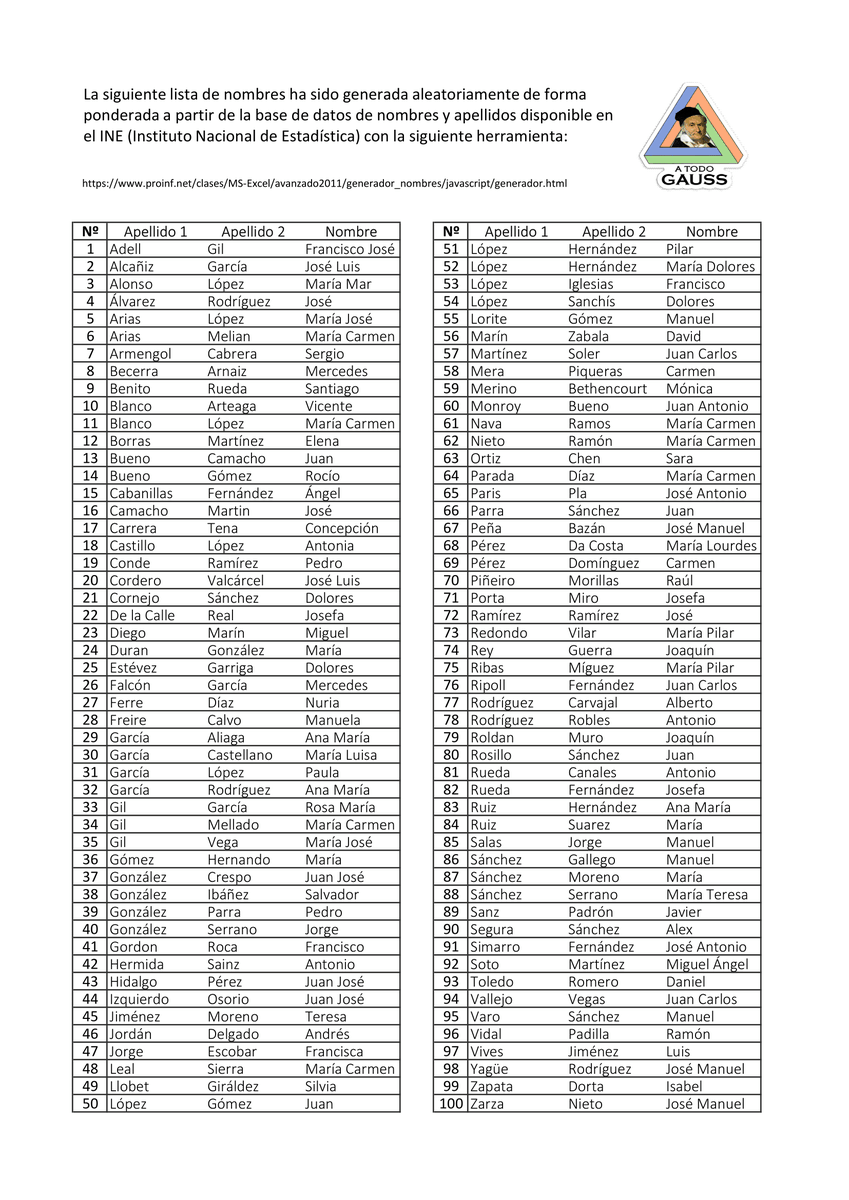
Listo, ¡vamos a asignar nuestras tres plazas!

¿Cómo lo hacemos? Vamos a hacerlo de dos formas distintas, por número (como defendemos todos los matemáticos) y por letra (como ha hecho la administración en el caso que menciona el periódico).

A ver que diferencias encontramos.

MÉTODO 1 (por números):
Se mete la mano en un saco y se saca una bola que llevará un número al azar, del 1 al 100.

Si sacamos el 27, ganan la plaza los números 27, 28 y 29.
Si sacamos el 2, ganan los números 2, 3 y 4.
Si sacamos el 99, ganan los números 99, 100 y 1.

Con el MÉTODO 1 todas las personas tienen LA MISMA PROBABILIDAD de obtener alguna de las plazas.

Asignamos las tres plazas al sacar una única bola, la probabilidad de que una persona concreta obtenga alguna de las plazas es de un 1%.

¿Y qué pasa con el otro método?

MÉTODO 2 (por letras):
Se mete la mano en un saco y se saca una bola que llevará una letra al azar, de la A a la Z.

Si sacamos la V, ganan la plaza Vallejo, Varo y Vidal.
Si sacamos el Z, ganan Zapata, Zarza y Adell (no quedan más con Z, así que pasamos a la siguiente letra).

Entonces ÁLVAREZ mira la lista y se da cuenta de una cosa:

Salga la letra que salga... ¡a él NUNCA le va a tocar!

Porque aunque saliese su letra, la A, ya están ahí ADELL, ALCAÑIZ y ALONSO para ocupar esas plazas. ¡INJUSTICIA!

¿Cuánta gente hay en esta situación?

¡En total hay 50 personas en esta situación!

¡LA MITAD de la lista está MATEMÁTICAMENTE ELIMINADA incluso antes de hacer el sorteo! ¡INJUSTICIA!

(Nota: no siempre saldrá exactamente el 50% la lista, en este caso ha sido coincidencia. Con otros datos podrá ser mayor o menor).

Bueno, y los otros 50... ¿al menos tienen la misma probabilidad?

Pues ni siquiera eso...

ÁLVAREZ conseguirá su plaza en un 0% de los casos (nunca).
ALONSO, en un 1,23% de los casos (cuando salga la A).
¡Pero ZAPATA lo conseguirá en un 4,94% de los casos! (cuando W, X, Y o Z).

Si comprobamos TODOS los casos posibles (según la letra que salgan) vemos que algunos nombres aparecen hasta 4 VECES, mientras la mitad de ellos ni siquiera aparecen en la lista:

En resumen:

EL SORTEO POR LETRA ES INJUSTO, DEBE SER ILEGAL.

El sorteo por número es justo. No cuesta más hacerlo bien: sólo hay que pintar números en lugar de letras en las bolitas.

¡FIN DEL HILO!

Gracias por leer. Si quieres preguntar o añadir algo, responde a este tweet 😘

PD: Con 100 no que es una burrada, pero con una clase de la ESO queda una actividad muy chula y útil para los estudiantes que están aprendiendo a usar porcentajes...

PD2: Soy yo uno de los 50 que quedan matemáticamente eliminados y llevo la denuncia al Tribunal de Estrasburgo 😂

Por cierto, hay un error en el suceso:

Dónde dice "la probabilidad de que una persona concreta obtenga alguna plaza" debería ser "la probabilidad de que una de las plazas sea obtenida por una persona concreta".

La otra probabilidad será mayor, pues hay 3 plazas sin repetición.

O más sencillo: multiplicad por tres todos los porcentajes.

En el CASO 1 la probabilidad sería de un 3% para todos.

En el CASO 2:
ÁLVAREZ tendría 0% (nunca).
ALONSO 3,70% (A).
ZAPATA 14,81% (W, X, Y o Z).

En cualquier caso, la proporción no cambia 👌