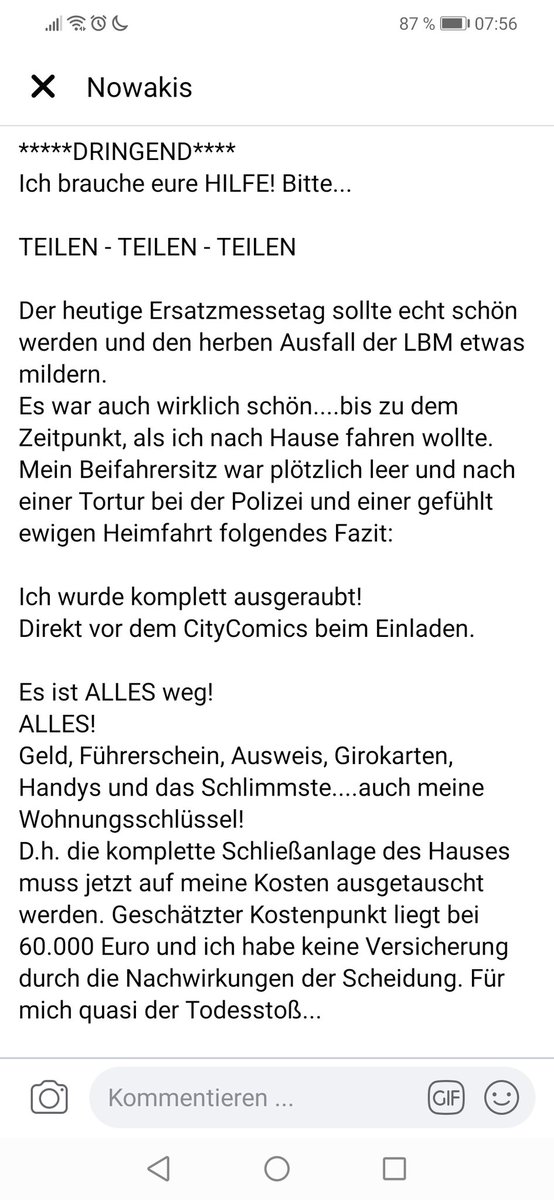
採用したモデルは「サイコロA,B,Cのどれかである」で事前分布でA,B,Cが等確率。サイコロA,B,Cの出目の分布は添付画像の通り。
しかし、推定先のサイコロXの出目の分布はサイコロA,B,Cからかけ離れていた。そして、推定・推測・推論にも失敗した。
そして、モデルが妥当であるかどうかで、統計分析が信用できるか否かが決まります。
これはベイズであろうがなかろうが同じこと。
仮説検定や信頼区間でも同じ。
A氏>我々は可能な限り努力して、妥当だと思われる確率モデルと事前分布を用いて、◯◯という仮説が正しい確率はほぼ100%になることを確認できました!
B氏>で、そのモデルが現実において妥当な証拠は?
A氏>我々はベイズ主義に基いて研究しているので、その質問には答えられません!
B氏>😱😱😱
A氏>我々は可能な限り努力して妥当だと思われるモデルを採用しました!そのモデルとデータから、我々は◯◯という仮説が正しい確率はほぼ100%であると考えざるを得なくなったということです!
B氏>努力したことは認めよう。でも、そのモデルが妥当な証拠はどこにあるの?
例えば添付画像のように「人文社会科学における確率モデルは云々」とも書いてあります。

その場合には分析用のモデル自体を更新した方がよい。
最初に採用したモデルを固定したままベイズ更新を続けても、妥当でない推論の収束先を得るだけ。
添付画像1
【ベイズ統計とは、標本を必ずとも必要としない】‼️‼️
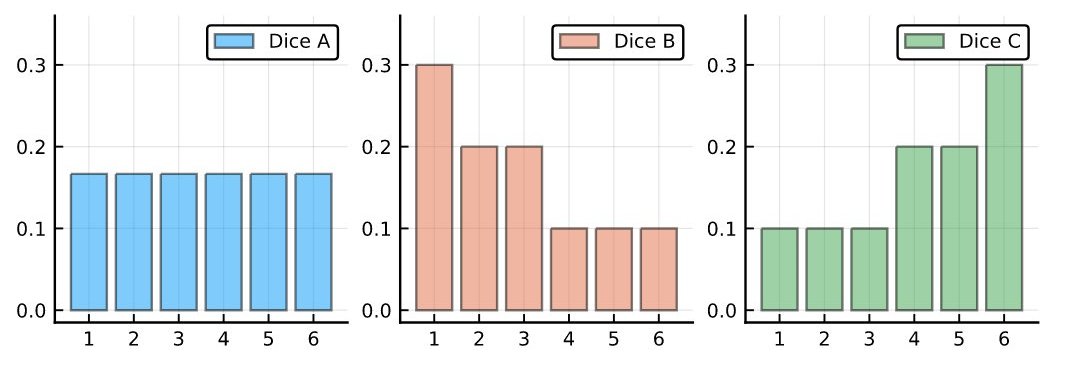
添付画像2は to-kei.net/bayes/ より。いつものデタラメが書いてあり、ベイズであることが極めて疑わしい肖像画が引用されているのも典型的。テンプレか?
添付画像3の正しい考え方は
watanabe-www.math.dis.titech.ac.jp/users/swatanab…
より。



twilog.org/genkuroki/sear…
を参照。相当に辛辣な批評になってしまっていますが、参考になれば幸いです。
統計学入門の教科書に問題があるので、問題のある教科書通りの解説を拡散すると必然的に批判されることになってしまう。
slideshare.net/yoshitaket/ws-…
ベイズ推定の概要@広島ベイズ塾
Yoshitake Takebayashi
Published on Mar 3, 2015
より。添付画像2によれば、母集団の母数も
【観察によって当然変わりうる】
らしい‼️‼️
添付画像3の正しい考え方は
watanabe-www.math.dis.titech.ac.jp/users/swatanab…
より(既出)。
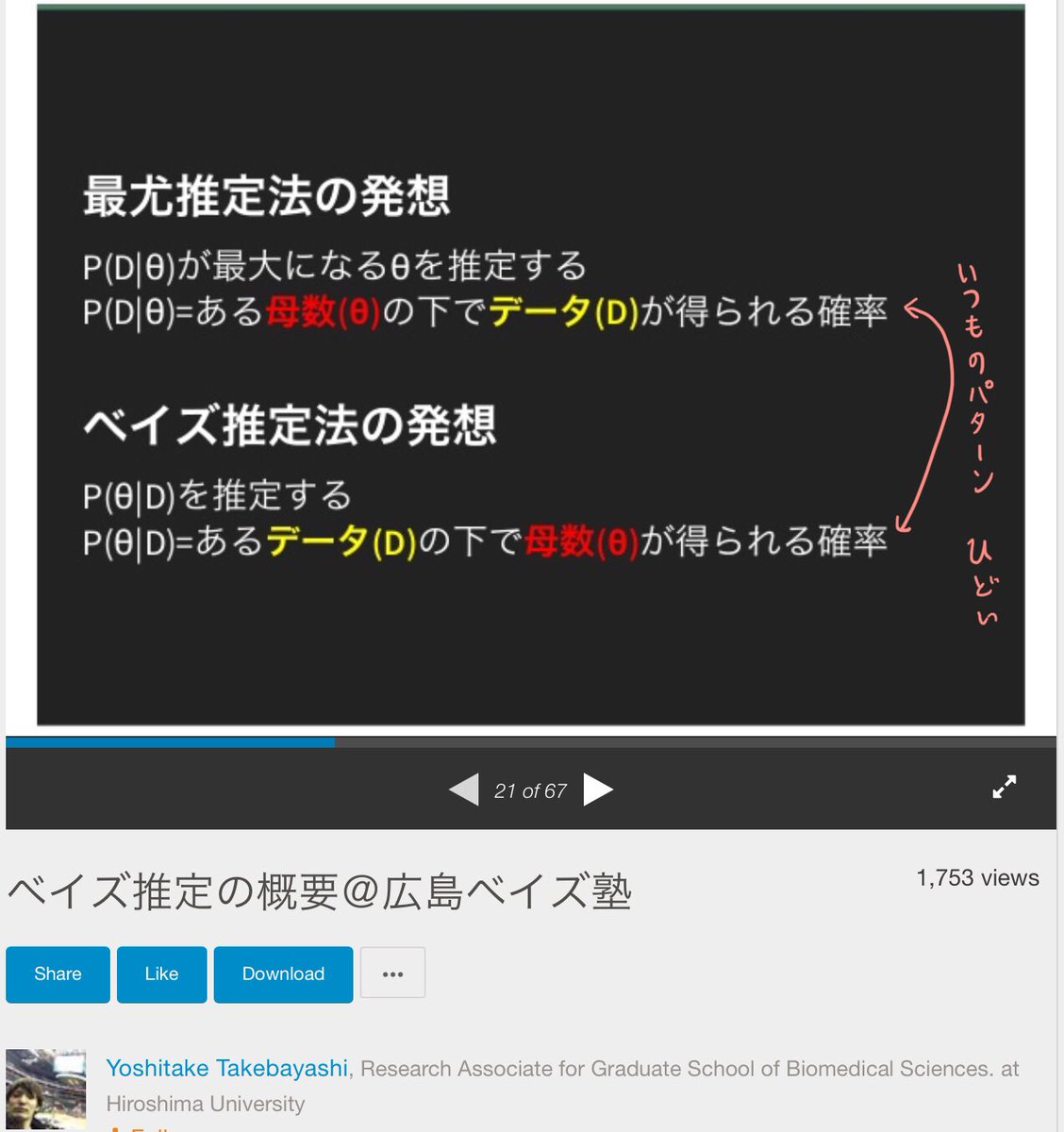
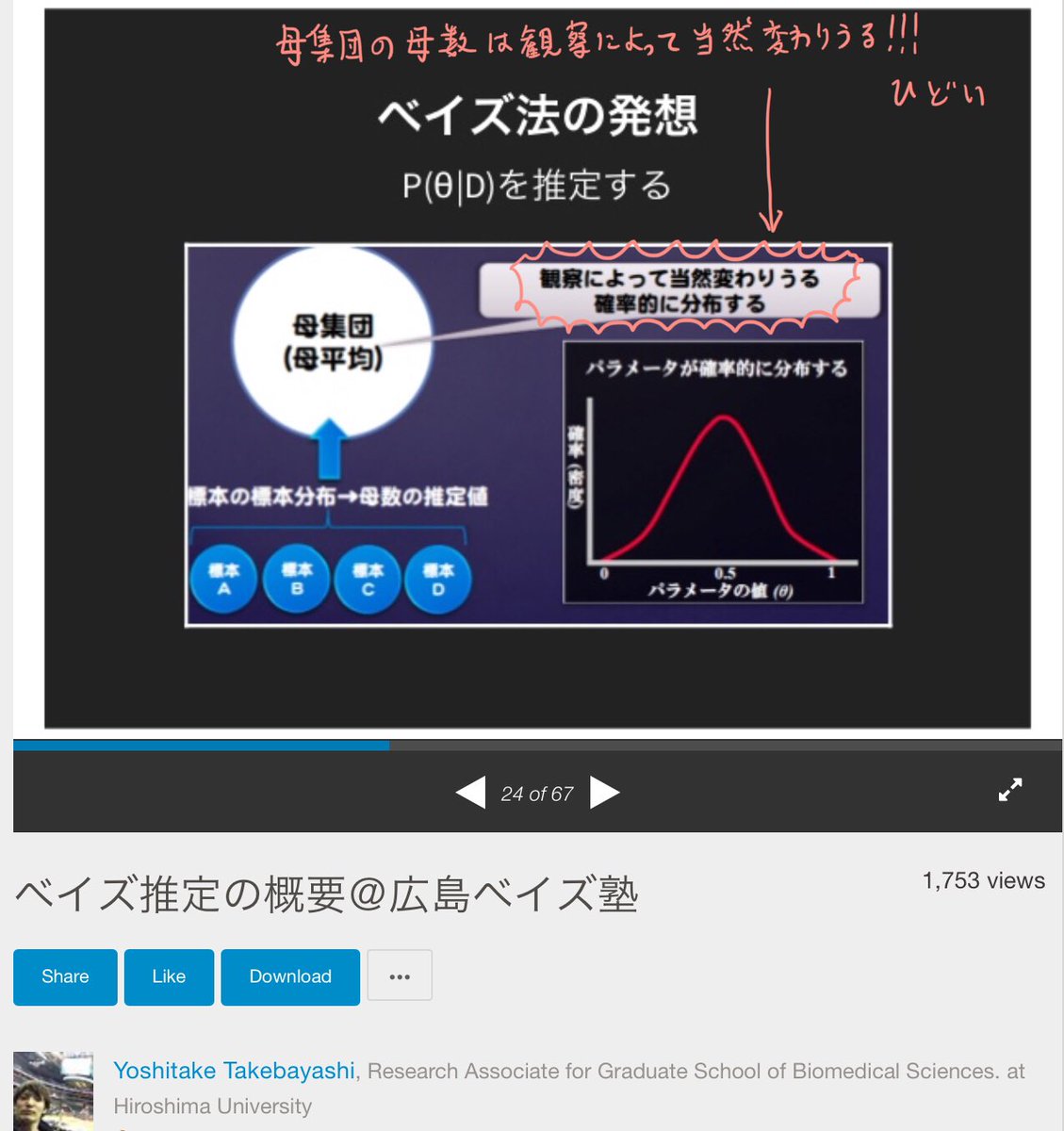

母集団からの無作為抽出したサンプルも、ベイズであろうがなかろうが、確率変数の実現値とみなされる。
事後分布は数学的モデル内部でのみ通用する確率分布に過ぎない。
誤解の蔓延は現時点で結構ひどいことになっているので、その責任を取る必要があると思う。
擬似哲学的な議論で分からないことを分かることにしてしまうのは非常にまずいというお話。
まずい統計学教育を何年も続けてやってしまった人はその逆向きを行う責任がある。
WAICについて知っているような人達の中にも、ベイズ統計について広まっている俗説を解説している人達がいる不思議。
未知の母集団分布に「正しい事前分布」なんてものはないし、事前分布はモデルの一部分なので、
「ベイズ統計では、モデルが正しければ、仮説が正しい確率を計算できる」
という主張をしても意味がない。
渡辺澄夫『ベイズ統計の理論と方法』7.1節の説明はミスリィーディング。
「仮説が正しい確率」なるものは最初からナンセンス。
救いようがない。続く
渡辺澄夫『ベイズ統計の理論と方法』を読めば、最尤法やベイズ法を使えば、サンプルサイズ→大で、採用した正しくないモデルの範囲内でベストの推定結果が得られることが分かり、さらにモデル間の相対評価の方法も得られる。
q(x_1)…q(x_n)
に従い、モデル内サンプルは分布
Z(x_1,…,x_n) = ∫p(x_1|w)…p(x_n|w)φ(w)dw
に従うという設定になっています。未知の分布サイドには事前分布というものがない。続く
∫P(x_1|w)…P(x_n|w)Φ(w)dw
型の分布に従うという設定を採用しています。この設定は同書の他の部分にはないものなので、この点に注意しないと読者はひどい誤解をしてしまう可能性があります。7.1節の内容は他の部分にはほとんど無関係です。
p.184 定理25では、上のZ(X_1,…,X_n)型の尤度の商を扱い、p.185 注意67(2)では事前分布がデルタ分布の場合を扱っており~続く
これを Z(x)=Z(x_1,…,x_n) (x=(x_1,…,x_n)) 型の分布に適用すればp.184 定理25が得られます。
genkuroki.github.io/documents/2016…
大学1年レベルまで初等化
nbviewer.jupyter.org/github/genkuro…
大学2~3年レベルまで初等化
❌ L(X) = p₁(x)/p₀(x)
⭕️ L(X) = p₁(X)/p₀(X)
例によって、x→Xの違いです。まあ、以上の説明で理解できる人はネイマン・ピアソンの補題を知っている人だけだと思うので、害はないと思いますが、念のために訂正しておきます。
∫P(x_1|w)…P(x_n|w)Φ(w)dw
の形ならば、事前分布がΦ(w)で確率モデル部分がP(x|w)の正しいモデルを採用できれば、パラメーターwに関する仮説が正しい確率を求めることができます。
しかし、この設定は同書の他の部分の設定と違う。
q(x_1)…q(x_n)
の形であるという設定では、事前分布がからむパラメータwがないので、「パラメータwに関する仮説が正しい確率」自体最初からナンセンスだということになります。モデル内部の仮想世界でのみそういう確率は考えられる。
みんな同じように変なことを書いているので、震源地があると思うのですが、変なことを書いている人達は参照文献を示さない習慣を持っているようなので、全然遡れないのだ。
何を読んで変な考えを知ったのかに関する情報をみんなで共有するべきだと思います。
21世紀の現代におかしなことを言っている人達は何を根拠にそういうおかしなことを言うようになったかが問題。
もしかして歴史的にのみ意味のある文献が根拠?
数学的証明にありがちなself-containedな説明でもない。
* 頻度論では母数は定数でデータは確率変数だが、ベイズ統計ではデータは定数で母数が確率変数になる。
というスタイルの説明です。これが一体どこから出て来たのかについては、歴史的にのみ意味を持つ文献さえ見当がつかない。
例えば、S市の小学6年生男子全員から30人を無作為抽出して、身長と体重のデータを得たとします。
そのデータをベイズ統計では分析した途端に、無作為抽出に伴うデータの確率的な偏りを考慮しなくなるのはおかしいです。続く
観測データを未知の分布を持つ確率変数でモデル化すると、ベイズ統計の事後分布も確率変数になり、モデルのパラメータは確率変数である事後分布に従う確率変数になります。
数学的な理解力が足りないと、そこから逃げるために「データは定数で事後分布は1つに確定している」などと間違った考え方に陥るリスクがあると思う。
そういう逃げ方はまずい。
文脈的に清水裕士さんが修正した原因は私だと思うのだが、そういう場合には影響を受けた私の発言にリンクを張って紹介しないと相当にまずいことをやっていることになります。その辺は大丈夫なのかな?
ブロックされた以降、彼が書いたものは読んでいません。
添付画像1は『パターン認識と機械学習 上』(所謂PRML)p.22より。ここにもよく見るデタラメな解説が!
添付画像2の正しい考え方はは渡辺澄夫の
watanabe-www.math.dis.titech.ac.jp/users/swatanab…
より。統計学ではなく、機械学習を勉強した人達の中にもおかしな考え方を学んで信じている人達が結構いるのかな?


ベイズであろうがなかろうが、データ集合自体が運悪く偏りまくっていたら、その学習結果も偏りまくる。

検定や信頼区間の代用ではなく、検定や信頼区間そのものの場合も数学的なモデルを前提にしないと意味のある結果が出せない場合が多いです。
検定や信頼区間の場合も使用したモデルの妥当性に無頓着なのは非科学的態度なのでやめた法がよいよと私は繰り返し言って来た。
仮に〇〇統計という分野で、信頼区間を求めるのに使ったモデルの妥当性に無頓着な態度が当然視されているならば、〇〇統計という分野は非科学的だということになる。
「パラメータの推定」という発想に「そのパラメータを含むモデルの妥当性を当然の前提にする」が付け加わると瞬時に非科学的な思考になる。
サンプルのサイズが大きくなると未知の分布の詳細な構造が見えて来る、というのが基本的な考え方。解像度が上がって来る。
未知の真の分布を本当にぴったり含む超複雑なモデルよりも、適切ない解像度のモデルの方が予測性能は高くなる。
モデルを前提にした分析をしているのに、モデルの妥当性について無頓着な態度
だと思います。数学的ではなく、常識的な意味で非科学的な態度を取っていることになる。
仮定しなくても、対数尤度にパラメータ数の違いよりもぅっと大きな差が付いていれば、対数尤度が大きなモデルの方を選ぶことは合理的だと思う。
統計学の使用はギャンブルであり、ギャンブルを他人に勧める人は正直に失敗するリスクを強調する必要がある。続く
AICはある意味でこの話の一般化になっています。
これを知っていれば、情報量基準と仮説検定が無関係でないことも分かる。
さらにシンプルなベルヌイ分布モデルで遊びたいなら
nbviewer.jupyter.org/gist/genkuroki…
が参考になると思います(#Julia言語)。
例の計算大事。
nbviewer.jupyter.org/gist/genkuroki…
にはベルヌイ分布モデル
p(x=1|w) = (x=1の確率) = w
p(x=0|w) = (x=0の確率) = 1-w
の場合に、AIC, WAIC, BIC, 自由エネルギーを計算しています。渡辺澄夫『ベイズ統計の理論と方法』を読むときに、このシンプルな例を知っていると少し楽になるはず。
どういう話になっているのか分かりませんが、私が既存の統計学入門への批判で繰り返し述べて来た「検定や信頼区間の解説で数学的モデルを使っていることの説明が不十分なせいで、モデルと現実の区別が曖昧になり過ぎている」という指摘に通じるものがあると思ったのでメモっておきます。
bookdown.org/sbtseiji/lswja…
jamoviで学ぶ心理統計
Danielle J Navarro & Dvid R Foxcroft
またしても「心理統計学」の事例。
【ベイズ流の視点では,統計的推論は信念の更新がすべて】という時代遅れで非科学的な考え方を信じている。



ameblo.jp/yusaku-ohkubo/…
A. Gelman "Philosophy and the practice of Bayes" の紹介
【・この時、事前分布は「事前の信念」であり事後分布は「仮説が正しい確率である」
2. しかし近年のベイズ統計においては、上のような見解を維持することが困難である】
【・事前分布はRIdge回帰やLASSO回帰のように推定値を安定化させるための道具であり、主観的な事前の信念を反映させるものではない
・事前分布は、事後予測分布などを通じて客観的に評価可能である
・事後分布は、「データが与えられた元での仮説が正しい確率」を教えてくれない】
ベイズ主義の下でのベイズ統計観は現代では時代遅れで、合理的な考え方が広まっていることについて、ゲルマンさん曰く
【3. 哲学者には、是非こうした近年のベイズ統計の動向を視野に入れて考察を深めてもらいたい】
せめて半世紀前の赤池弘次さんくらいまでは追いつくべき。
nbviewer.jupyter.org/github/genkuro…
watanabe-www.math.dis.titech.ac.jp/users/swatanab…
および以下のリンク先のリンク先
【事前分布は「事前の信念」であり事後分布は「仮説が正しい確率である」】という考え方をする必要はない。
時間の無駄なので読む必要はないが、豊田秀樹さんの本を絶賛している。内容的にもかなり呆れたものだ。
怖いのはこのブログ記事のような感覚で学生に「ベイズ統計」(もどき)について教えているかのうせいがあること。
kosugitti.net/archives/5211
妥当かどうか不明の確率モデルを使って、信念の度合いを確率で表現した事前分布を事後分布に更新した結果を本当に信じているとしたら、その人は合理性に欠けた精神の持ち主です。続く
要するにベイズ主義とやらはつまらないナンセンスなことを大真面目に考えているだけだと思う。
非現実的なトイモデルとしても苦しい。
これを知っていたら「仮説が正しい確率が分かる」とはとても言えない。
しかし、三浦麻子さんは、三浦さんが筆頭著者である
team1mile.com/sjpr61-1/
→ team1mile.com/sjpr61-1/miura…
に添付画像のように書いてあることの学問的責任は取らなければいけなくなるだろうと思いました。

詳しくはこのツイートがぶら下がっているスレッド全体を参照。続く
尤度の定義は「確率モデル内の仮想世界で現実から得たデータが生成される確率(密度)」で「確率モデルのデータへの適合度」を意味します。
尤度解説1↓
信頼区間の計算に使った確率モデルの標本分布で測った確率を考えると95%信頼区間に真の値が含まれる確率は(約)95%になる。続く
多くに場合に曖昧で混乱を招く原因になるので、「何で測った確率なのか」のも説明しながら「確率」という言葉を使った方が親切。
これは大学での統計学教育の闇の一部分です。
日本語圏だけの問題では__ない__点が怖い。
この点は「頻度論」の95%信頼区間の方が分かり易いです。
scholar.google.com/scholar?cluste…
Andrew Gelman and Cosma Rohilla Shalizi
Philosophy and the practice of Bayesian statistics
2010
あちこちからダウンロードできますね。
ベイズ統計に関しては半世紀程度時代遅れっぽい解説の方がスタンダード。
赤池弘次さんや渡辺澄夫さん的な考え方は無視されているように見える。
「主観的事前分布」「無情報事前分布」というような説明をしているだけで私はアウトだと感じる。
1. ベイズの定理によって事前分布における信念の度合いが更新され、事後分布によって仮説が正しい確率を計算できる。
2. 主観を入れたくなければ無条件事前分布を使うべし。
3. 様々なベイズ推定量はリスク最小化によって合理的に正当化される。
ベイズ更新後に事後分布で仮説が正しい確率を計算して終わりにするには科学的に非常識で、普通は事後分布を求めた後にモデルのチェックを慎重に行う。

下手をすれば「専門家」の間でもそうかもしれない。
Z(x_1,…,x_n) = ∫p(x_1|w)…p(x_n|w)φ(w)dw
に関するリスク(←別に決めておく)の期待値の最小化です。
どこにも推定先の未知の(真の)確率分布は出て来ない!
モデル内の非現実的設定でのリスク最小化。
そういうつまらない話をよく見る。
現実世界とは縁が切れた純粋にモデル内部における議論でしかない。
❌無条件事前分布
⭕️無情報事前分布
ベイズ統計のユーザーは自分が採用した事前分布を「主観的事前分布」「無情報事前分布」に主観的に分類して満足せずに、採用した事前分布を使った推定・推測・推論の性質を確認した方が無難かも。
さらに、「無情報事前分布」にはJeffreys事前分布(1(w(1-w))と一様分布のちょうど中間に位置する事前分布)という有力な選択肢があります。
そうではなく、事前分布もモデルの立派な一部分であり、採用した事前分布によってモデル全体がどのような性質を持つことになるかを理解しておく方が重要。目的によって使い分ければよい。
しかし、結果に無視できない違いが生じる可能性があるなら、目的に応じてどちらが優れているかを考える必要がある。
「無情報事前分布vs.主観的事前分布」という「頻度論vs.ベイズ」という非科学的な発想のサブセットを捨てるべきだと思います。
検定や信頼区間で正規分布モデルを安易に前提にする行為は「非科学的だ」という意味で主観的。
実際の「米国統計学会の統計的有意性とP値に関する声明」の実質的内容は「P値入門」になっていて、それを読めばP値の概念をより正確につかめ、誤用する心配もなくなる類のものですよね。
ベイズ云々と無関係にこういうことは大事だと思う。続く
biometrics.gr.jp/news/all/ASA.p…
にあります。
検定について教えなければならなくなった人にとってこれは非常にありがたい翻訳だと思いました。
仮説検定自体はシンプルな数学的道具の1つに過ぎず、仮説検定自体に罪はない。
仮説検定を別の何かに置き換えても、ずるをした方が有利な状況がそのままなら、ずるをする人達が必ず出て来ると思う。
r(x|z) = ∫p(x|w)φ(w|z) dw
と積分で表されることになり、表に出ているパラメータzの事前分布としてψ(z)が採用されている場合になります。
その手の誤解はStanでモデルを書くときに生じる可能性があると思う。続く
(1) Zが分布ψ(z)に従ってランダムに生成される。
(2) k=1,…,nについて、W_k が分布 φ(w_k|Z) に従ってランダムに生成される。
(3) k=1,…,nについて、X_kが分布 p(x_k|W_k) に従ってランダムに生成される。
Stanなどではこれを素直にコード化できる。続く
これがひどい誤解である理由は w_k はモデル内部で積分されて消えることを見逃しているからです。続く
r(x|z) = ∫p(x|w)φ(w|z) dw
を使うと、
(1) Z が分布ψ(z)に従ってランダムに生成される。
(2) 必要なくなる。
(3) k=1,…,nについて、X_kが分布r(x_k|Z)に従ってランダムに生成される。
と書き直される。
「だったら、最初からw_kを消して、階層ベイズとか言わなければいいのに」と思う人がいるかもしれませんが、モデルを数値的に解くためには「階層ベイズ」という見方が有効なのです。
r(x|z)=∫p(x|w)φ(w|z)dw
と積分表示されているので、モデルを直接的に数値的に解くためには、この積分を数値的に求める必要が生じます。
r(x|z) が初等函数や有名な特殊函数で書けるなら、r(x|z)のコンピュータでの計算は易しくなります。
一般にはそうではない!
r(x|z) = ∫p(x|w)φ(w|z)dw
と書けているとき、
(i) r(x|z)をコンピューターで楽に計算できるなら、w_k達を持ち出さずに数値的にモデルを解ける。
(ii) そうでなくても、階層モデルのスタイルでMCMC法を使えば事後分布のサンプルを作れる。
続く
ベイズ統計にはこのようなテクニカルなメリットがある。
(A) 事前分布 φ(w), 確率モデル p(x|w)
(B) 事前分布 ψ(z), 確率モデル r(x|z) = ∫p(x|w)φ(w|z)dw
の違いと関係についても説明しておきましょう。
(B)の場合については既に詳しく説明したので、(A)のモデル内でのサンプルX_kの生成の仕方を説明します。続く
(1) Wが分布φ(w)に従ってランダムに生成される。
(2) k=1,…,nについて、X_kが分布p(x_k|W)に従ってランダムに生成される。
これと以下のリンク先の(B)の場合の注目するべき違いはWとW_kの違いです。続く
それに対して、階層モデルの(B)の場合に、X_k達は(一般には)互いに異なるパラメータ値W_kで決まる分布p(x_k|W_k)で生成されます。
(A)と(B)の違いは、(B)では各kが異なる「個性」を持つことだと言える。
このとき、すべての科学者の測定技術が同等で同じ程度の誤差で測定できるという想定でモデルを作ると(A)型になります。
科学者ごとに測定技術に違いがあると想定すると(B)になる。
その場合には、r(x|z)を直接コンピュータで計算できるようにモデル化することもできるだろうし、階層ベイズ化してMCMCをぶん回す方法も使える。
nbviewer.jupyter.org/github/genkuro…
で解説し、数値例を作ったStein推定では、n個の別々の期待値を持つ分散1の正規分布でX_1,…,X_nが生成されると想定しているので、「個性」を考える(B)の話に関係しており、この場合も渡辺澄夫さんのベイズ本の範囲内の話題になります。
nbviewer.jupyter.org/gist/genkuroki…
測定スキルの異なる7人の科学者たち
このノートではまさに以下のリンク先の問題の練習問題を扱っています。(B)でr(x|w)の積分後の結果が分かっている場合なので、ベイズ法ではなく、最尤法を使いました(へそ曲がり(笑))。AICとLOOCVも計算しています。
nbviewer.jupyter.org/gist/genkuroki…
測定スキルの異なる7人の科学者たち
のベイズ統計版のノート(計算&プロット)を作れば勉強になると思います。WAICやLOOCVも計算する。
さらに(B)で(ii)の方法も使ってみて、(i)の結果と比較して一致することを確認するとよいと思う。
❌1(w(1-w))
⭕️1/(w(1-w))
パラメータ0≦w≦1のベルヌイ分布モデルの共役事前分布は
w^{a-1} (1-w)^{b-1}
の形。定数倍部分は本質的でないので省略。
a=b=0の場合の、両端のw=0,1に分布の集中度が最も高い場合の事前分布が最尤法に対応しています。続く
Jeffreys事前分布(a=b=1/2)では、以上の2つの場合の中間になる。続く
nbviewer.jupyter.org/gist/genkuroki…
より。平均予測誤差(KL情報量の平均)と平均二乗誤差のプロット。サンプルサイズがn=10,20,50の場合。MLEは最尤法、Bayes(0.5,0.5)がJeffreys事前分布、Bayes(1.0,1.0)が一様事前分布の場合。
1つ前のツイートで説明した通りになっています。
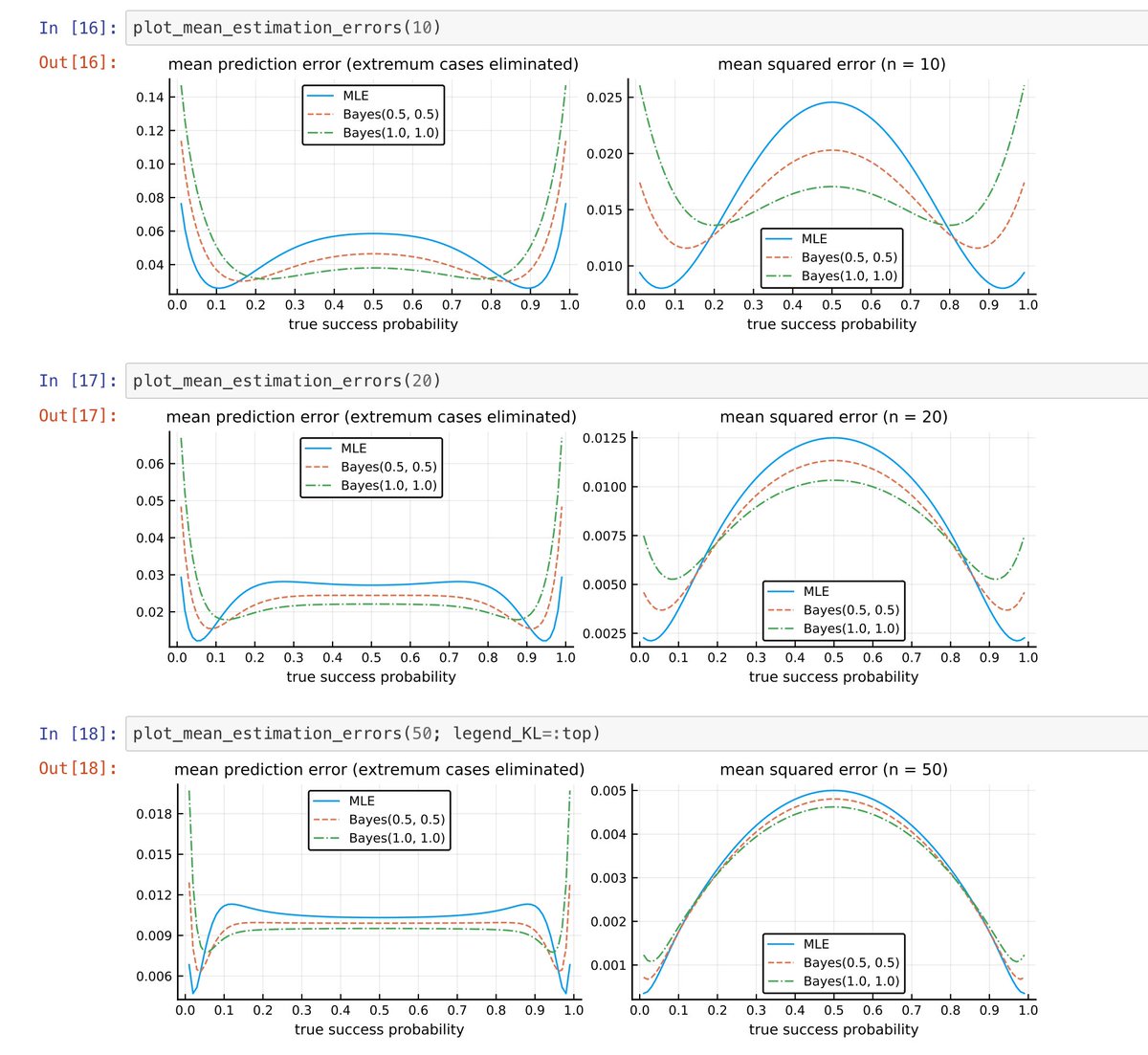
そういう計算を実際にしてみて、百聞は一見に如かずの精神で、観察を積み重ねれば様子がわかる。
こういう考え方は「事前分布は主観を表現している」という発想にこだわると出て来なくなる。
Normal→二項分布の正規分布近似で定義したP値
Posterior→ベイズ統計の事後分布に関するP値の類似物
2つの線の一致は「頻度論」信頼区間と「ベイズ」信用区間の一致を意味する。
「頻度論」でのP値信頼区間
と
「ベイズ」でのP値の類似物と信用区間
はよく一致しています。
「頻度論」でp-hacking可能ならば「ベイズ」でも全く同じ方法で可能です。
ずるをした側が得をする環境では、ずるをするやつは必ず出て来ると思う。
そして、嘘がばれ難くするには、嘘をついた人自身も嘘をついていないと信じていた方がよい。
ああ、いやだ、いやだ。
What’s wrong with Bayes « Statistical Modeling, Causal Inference, and Social Science statmodeling.stat.columbia.edu/2019/12/03/wha…
ベイズ統計に関するそれらの【とにかくわかりやすかった説明】は(厳密には具体的にどういう説明なのか特定する必要がありますが)、ことごとく間違っていたと判断する方が無難だと思いました。本当はすっきりしようがない話のはずなので。
「騙された!」と感じることは結構大事なことかも。
信頼区間を正しく理解してますか?
確信区間との違いって何ですか?
qiita.com/katsu1110/item…
「ベイズ統計では仮説が正しい確率がわかる」
「頻度論の信頼区間より、ベイズ信用区間の方が解釈が容易で分かり易い」
の様なデタラメを学生に言えなくなるだけ「萎縮」してもらえたら、とてもうれしいです。😊

この点に関しては非常に要注意。
watanabe-www.math.dis.titech.ac.jp/users/fujiwara…
特異モデルにおけるベイズ検定と変化点発見への応用
藤原香織 渡辺澄夫
の話は「仮説検定とベイズ統計は水と油だ」のような印象論が__誤り__であることの証拠になっている。
間違った印象論を広めるような教育はまずい
asakura.co.jp/books/isbn/978…
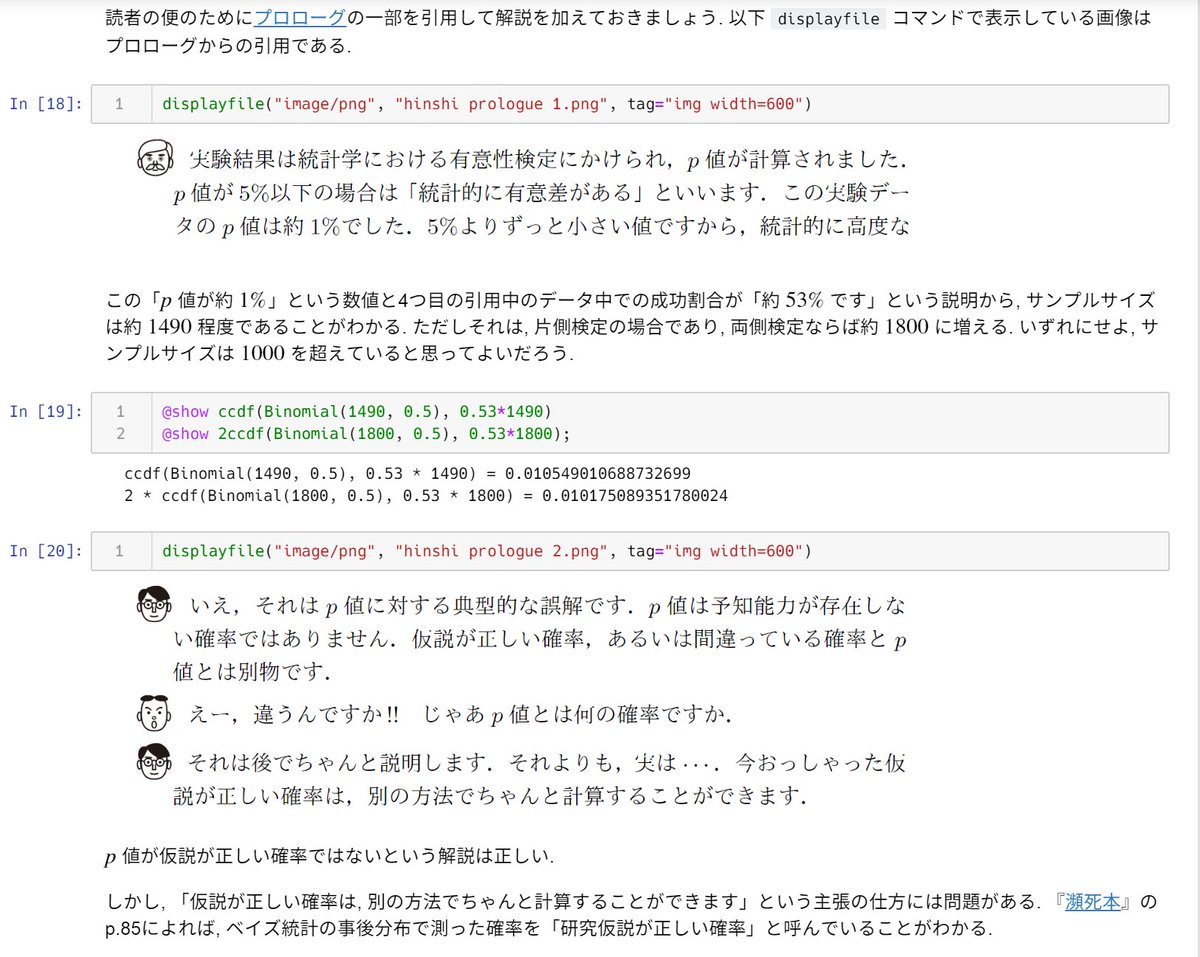
で公開されている豊田秀樹『瀕死の統計学を救え! 』のプロローグを見てみました(添付画像に引用)。
ひどかった。
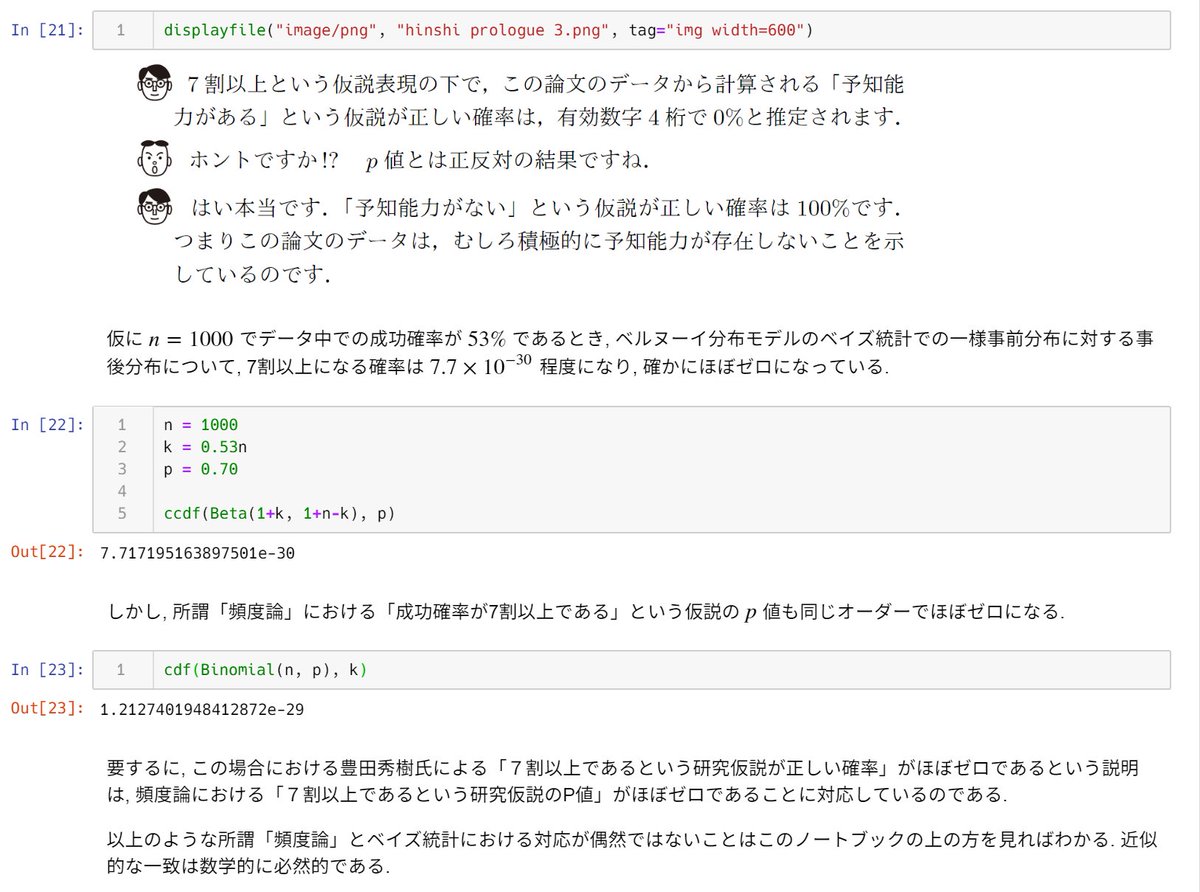
ベムの超能力論文の話。まず的中率5割の帰無仮説のP値は1%と非常に低かったという話をしています。nは1000のオーダーであることがわかる。続く



そして、的中率が7割以上という仮説が正しい確率はほぼ0だと計算され、【「予知能力がない」という仮説が正しい確率は100%】と結論します。
色々ひどい。



あれ?P値って仮説が正しい確率ではないですよね!



豊田秀樹さんはデタラメを書いていると思いました。



それらはほとんど一致!
ベイズ統計を使えば所謂「頻度論」では出せなかった強い結論を出せるという考え方は完全に誤り。
nbviewer.jupyter.org/gist/genkuroki…
で公開していています。
ベイズ統計のWAICから作ったP値の類似物もn=100で所謂「頻度論」のP値にほぼ一致していること
を示す動画もそちらにはあります(笑)。こういう動画作成は徹底した方が楽しい。
「頻度論vs.ベイズ」的な発想自体が根本的に時代遅れで間違っているわけです。
シンプルなモデルの特徴。
norimune.net/3339
「研究仮説が正しい確率」について
を見てみました。
論外にひどい内容だった。
分かり易い部分を添付画像に引用。
【頻度主義】とやらの意味が不明。

そういう「こったこと」をやらずに、気持ち良く議論したいものだと思いました。
このスレッドでも少し上の方で「的中率が7割以上」という仮説の検定(片側検定になる)のP値を話題にしています。

なるほど、こういうレベルで所謂「頻度主義」を理解したつもりになっているから、論外な議論もきっちり否定できないのかと思いました。
こういうことも多分知らないのではないか?
清水さんが共著者の1人になっている『社会科学のためのベイズ統計モデリング』は良い本だと思います。
特異モデルの場合に事後分布は単峰型にならず、非常に複雑な形にもなりえます。だから「パラメータの推定」という発想は有効ではなくなる。続く
一方、事後分布が単峰型になる場合には、所謂「頻度主義」の最尤法や信頼区間とベイズ統計はほぼ同じ結果を出します。所謂「頻度主義」を真に超えたことをベイズではできなくなる。続く
これ、やっぱり、相当にひどい話だと思いました。
本質的に同じ結果が得られるなら楽な方がよい。
github.com/kosugitti/psyc…
「はじめに」(添付画像)に
【母数を知るための推測 大学での統計,心理統計は~母集団を表す数字を求めるための推測統計である。】
と書いてあって、「ああ!またか!」と思いました。

現実の未知の母集団から得たサンプルを使って、モデルのパラメータ(現実の未知の母集団をあらわす数字ではなく、モデルを表す数字)を推定すること
を意味し、モデルの妥当性が不明な場合には、その推定結果の妥当性も不明になります(当たり前)。
こういう当たり前のことが大事だと思う。
初学者を混乱させる説明の仕方
↓
母集団分布は正規分布であると仮定する。
正直かつより正確な説明の仕方
↓
未知の母集団分布について推定・推測するために正規分布モデルを利用する。母集団分布とモデルの正規分布を混同しないように注意して欲しい。
母集団分布が未知である状況では、正規分布モデルを使った推定が妥当であるかどうかは不明になる。ゆえに、正規分布モデルを使った推定結果を客観的に信頼できると信じてはいけない。統計学は不良設定問題を扱うので、こういう点に注意し続ける必要がある。
「母集団分布は正規分布であると仮定する」
と書いてあるのを見て、
えっ?正規分布だと仮定しちゃっていいの?
と思った人は多いと思う。当然そう思うべきで、思わなかった人は危ない状態に陥っている。
実際には、推定用の数学的モデルとして正規分布を使っているだけで、母集団分布は未知のままだと思ったままで推定作業を行うのです。サンプルの様子を見て正規分布モデルが妥当でないと分かることもある。
「母集団分布は正規分布であると仮定する」
と書いてあるのを見て、
えっ?正規分布だと仮定しちゃっていいの?
と思わずに受け入れてしまった人は自分自身の洗脳を解く必要があります。そして学生時代に受けた統計学教育に疑問を持つべきだと思います。
「統計分析は何らかの仮定がないと不可能である。ゆえにここでは母集団分布は正規分布であると仮定する」
という回答は
非科学的な詭弁
に過ぎない。そういう回答をして来た統計学教師は学生に集団に批判されるべきだと思います。
「教科書には確かにそう書いてあるが、実際には母集団分布が正規分布になっていると仮定したりしない。正規分布モデルの妥当性は常に疑われ続ける。分析の過程でサンプルおよび他の様々な情報によって正規分布モデルの使用の妥当性が崩れることもある」
だと思います。
正規分布モデルの妥当性を疑うことができない人には統計学を使って欲しくないです。
github.com/kosugitti/psyc…
【心理学データ解析基礎1/2
担当:小杉考司
2020年2月20日】
より。一様事前分布の場合のベイズ推定値が最尤推定値に一致すると書いてあるが、ずさんな説明。正しくはベイズ統計とは異なるMAP法の推定値が一様事前分布のとき最尤法と一致するだけ。


【モデルがそもそも間違っていればその推定値が正しい保証はない】
と書いてあるのに、その続きが、ゆえに心理学においても統計分析に用いたモデルの妥当性を常に疑い続ける、ではなく
【心理学の場合は~誤差に正規分布を仮定するものがほとんどである】
😱😱😱

異なる分析ツールX,Yについて、ある場合にはX,Yを用いた結果がほぼ同じで、別のある場合には全然違うとしよう。
そのとき、X,Yの両方をBと呼ぶだけで終わるようでは、読者はX,Yの道具としての違いを認識できなくなります。続く
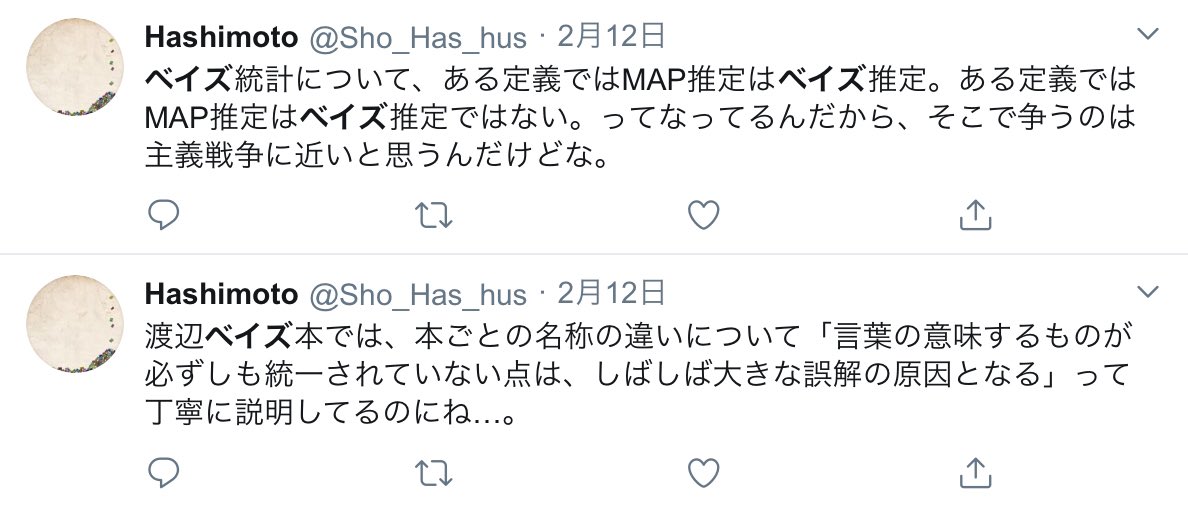
続く
* 異なる道具の区別を明瞭に説明しない。
* 「ベイズ統計」と名付けた途端に不可能だった強い主張をすることが可能になると説明する。
としていることが批判されているわけ。
「ベイズ統計」という用語の使い方が杜撰であること
や
そもそもまともに科学的な考え方をできていないんじゃないかという疑いがあること
を批判しているのであり、「ベイズ統計」と名付けることそのものを批判しているのではありません。
私が、ベイズ云々だけにこだわっているのではなく、ベイズに限らない統計学入門のスタイルを批判していることを思い出して下さい。
だから、その辺についての説明も必要になりました。
その辺はかなり重たい作業になりました。続く
少なくとも研究の再現性の問題はそれでは絶対に解決しない。
この性質を説明せずに「ベイズ統計では仮説が正しい確率が分かる」などと解説するのはひどい。
数学的モデル内部ではいくらでもナンセンスなことが起こり得るので、事後分布で計算した確率が有益な指標にならない場合があっても不思議でもなんでもない。
その外部から得たデータと比較できるものの確率分布
と
その外部に比較対象がないものの確率分布
に分類されます。事前・事後分布は後者の分布であり、それそのものをデータと比較することは不可能なのです。間接的にその妥当性を調べるしかない。
確率モデルが大外ししていると、事後分布からミスリーディングな結論が得られてしまうのです。
特に、モデルと現実の区別が曖昧で、モデルの妥当性の吟味が必要であることを徹底的に強調しようとしない非科学的な態度が問題だと思います。
母集団分布は正規分布であると仮定する
と書いてあることが多くて、
えっ?正規分布だと仮定していいのかよ?
という真当な疑問を蔑ろにするスタイルが標準的であることに気付くわけです。正規分布はモデル内確率分布に過ぎません。
ベイズ統計の名の下で
事後分布の代表値を求めることや
事後分布で『仮説が正しい確率』を求めること
を特に強調して済ませること
を批判しています。
もしもそういうスタイルが妥当であるとお考えならば、意見が正反対であることになります。
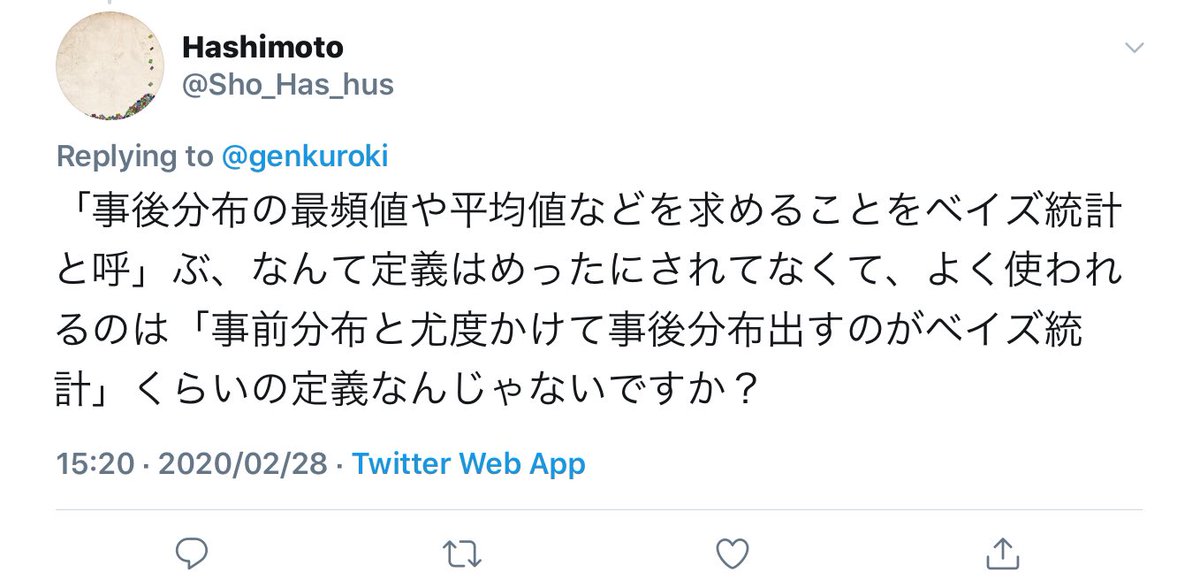
ベイズの定理を形式的に適用すると、ベイズの定理よりも基本的な条件付き確率分布の概念が見えなくなります。続く
事前分布と尤度函数から事後分布を作る手続きを特に強調すると、この点が見えなくなりがちだと思います。
(1) 数学的モデルを使ってデータからの推定・推測・推論を行う。
(2) その妥当性を吟味する。
「事前分布と尤度函数から事後分布を作って、事後分布の代表値を求めたり、事後分布での確率を計算する」は(1)に属することで、(2)は別に行う必要があります。
(2)が難しくて重要な部分。
島谷健一郎著『ポアソン分布・ポアソン回帰・ポアソン過程』
統計スポットライト・シリーズ2、近代科学社、2017、iv+124頁
amazon.co.jp/dp/B076LVLLSF


ポアソン過程モデルによる推定を詳しく解説した後で
【5.8 正解はなくてもモデルを創る
~そもそもこれらの樹種がポアソン過程に従って分布している可能性は皆無である~こうした影響を考慮したモデルを考案したり、その検証に有効なデータを~】


* 離散分布の中で最も基本的な確率分布だと思われるポアソン分布についての易しい解説
* ポアソン分布モデルを例に使った最尤法入門
* ポアソン回帰を例に使ったAIC(所謂赤池情報量規準)入門
* 非定常ポアソン過程とその応用
そして、全編に渡って、真の分布が未知であることを強調した解説がされています。
この本を読んで、実際に数値実験してみて、結果とソースコードを公開する人が出て来たり、そのベイズ版も試してみる人が出て来ると、さらに楽しくなりそうな本だと思いました。
それなのに、その確率を「仮説が正しい確率」などと呼ぶのはまずい。
上で紹介した島谷「ポアソン³」本は、当たり前であるべき話を「ポアソン尽くし」の本を書くことによって説明することを試みた本とみなせると思いました。
意思決定論によるベイズ推定の説明は絶対に鵜呑みしてはいけません。
そして、安全牌は「事後分布による確率モデルの平均を予測分布とみなすこと」です。
事後分布の平均(EAP)を推定値として採用するのはとても危ない。
これも私には単なる常識的配慮に過ぎないと思うのですが、どうでしょうか?
リンク先の添付画像の一部をこのツイートに添付。豊田秀樹さんは「共通した標準偏差を持つ2つの正規分布モデル」と「十分に広い範囲の一様事前分布」から作った事後分布で計算した確率を「研究仮説が正しい確率」と呼んでいます。
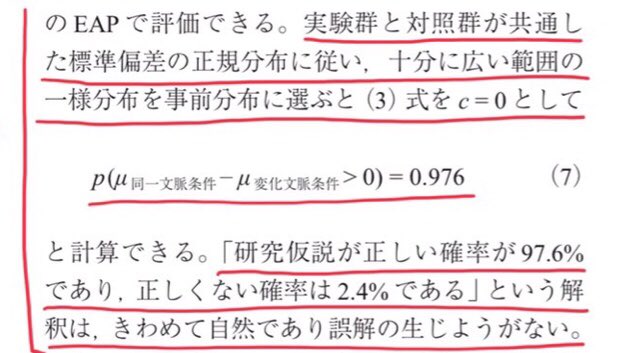
それに対して通常のP値や信頼区間が何を意味しているかはずっと分かり易いです。
未知の確率分布で生成されたサンプルを扱うベイズ統計
と
有病率と有病者の陽性率と無病者の陰性率からの陽性者が有病者である確率の計算
では難易度が段違いであることを知っておくべきです。後者は大学入試でも出題される程度に易しく、前者は難解です。
モンティ・ホール問題
も確率計算としては易しい話です。
その手の易しい話と、未知の確率法則が生成したサンプルを扱うベイズ統計では難易度が違い過ぎるので、無関係の話題だと思った方がよいです。
多くの伝統的解説はその意味で誤解に誘導する内容になっています。
島谷健一郎『ポアソン分布・ポアソン回帰・ポアソン過程』(2017)はコンピューターシミュレーションでも遊べるくらい具体的な例を通して、基本的かつ普遍的な考え方を解説している気持ちの良い本です。
数学が得意な人が娯楽で読むには非常に良い本だと思う。
パラメータに関する事後分布の平均は
パラメータ空間の座標の取り方に強く依存します。
事後分布の台が凸型になるかどうかも座標の取り方に依存。
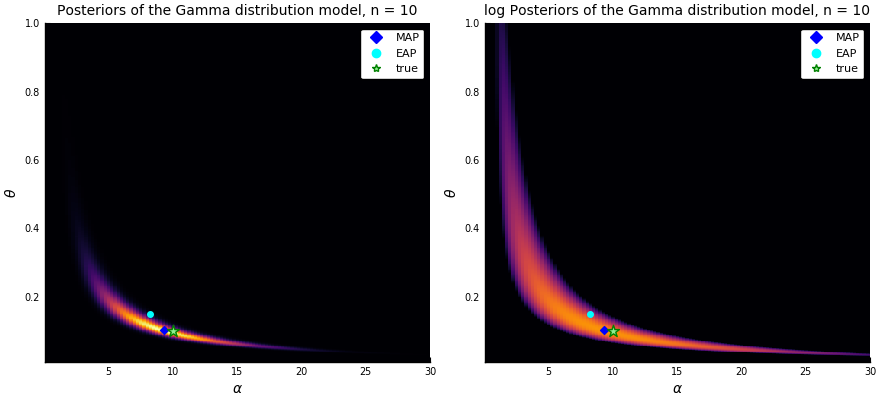
事後分布の平均(所謂EAP)を推定値として採用することはこの意味でもかなり危険です。具体例に続く
☆が真値、◆がMAP推定値(今の場合は最尤推定値と同じ)、◯は事後分布(posterior)の平均(=EAP推定値)です。
EAP推定値が事後分布の台から外れていることに注目。
☆が真値、◆がMAP推定値(今の場合は最尤推定値と同じ)、◯は事後分布(posterior)の平均(=EAP推定値)です。
EAP推定値が事後分布の台から外れかけている。
#Julia言語 ソースコード↓ (汚いです)
nbviewer.jupyter.org/gist/genkuroki…
選択肢が多い場面では至る所に落とし穴が隠れているので要注意。
リスク最小化を「主観に基く合理性」だと解釈して、「主観主義」によって「ベイズ推定」を説明している文献は沢山あるので要注意です。
引用【最適なパラメータの集合が凸集合でないときには、平均プラグイン法は統計的推測には適していないので注意が必要である】
対数を取って確認したら(添付画像の右半分)、左側と上側に結構のびていました。
足し上げ時の重みが小さくても遠く離れていれば平均には影響を与えることができる。
to-kei.net/bayes/decision…
決定理論とは?簡単にわかりやすく説明
to-kei.net/bayes/bayes-es…
ベイズ推定量は、事後分布の平均と一致する
(互いに相互リンク)
などがあります。
Z(x_1,…,x_n) = ∫p(x_1|w)…p(x_n|w)φ(w)dw
に従って生成されているという設定での平均リスク最小化を扱うことになる。q(x)との関係は一切考慮しない。
その結果、EAP推定を勧めて来たりするわけ。
現実での予測の失敗には一切配慮せずに、主観内部でリスクが最小化できれば合理的だとみます方針。
数学をよく知っているほど、そういうことがわかって来るので、数学をよく知ってるせいで「おお!なるほど、これは合理的だ!」と感じて騙される可能性がある。
この辺は本当に要注意な部分だと思う。
ベイズにしても研究の再現性の危機の問題が解決しないことは自明だと思う。
ベイズ統計を理解していない人だけがベイズにすればバラ色であるかのようなことを言えるのだと思う。
理解している人が適切に使えば強力な道具になり得るとは思いますが。
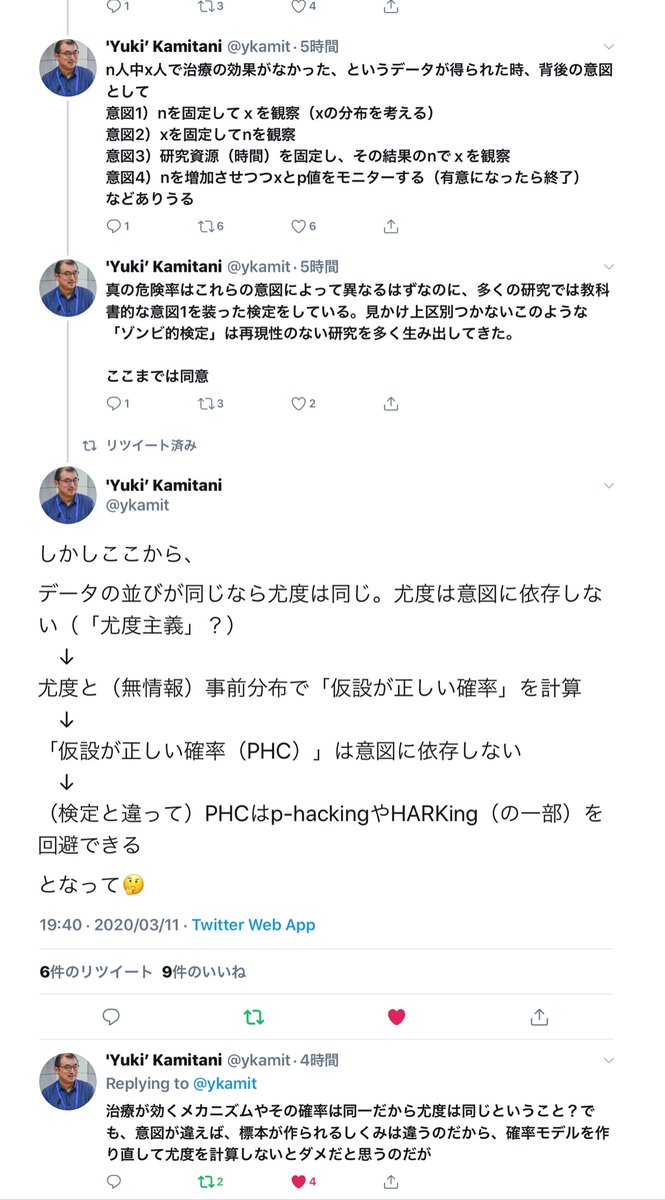
意図1~4で異なる確率モデルを使う必要があるのは、ベイズであろうがなかろうが同じこと。めちゃくちゃ、当たり前の話。
(1) 通常の「頻度論」での信頼区間と同じ意味での確率(モデル内標本分布で計算した確率)
と
(2) おとなしめの事前分布でのベイズ統計での事後分布で計算した確率
が互いに相手をよく近似することを示せます。
要するに、ベルヌーイ分布モデルのような単純なモデルでは、ベイズ統計を行っても新しいことは出て来ないということ。
プロローグでベイズ統計を使っている部分は(「7割以上云々」の部分)は「頻度論」の片側検定と本質的に同じことです。
公開されているプロローグだけでひどい内容であることが一目瞭然だと思う。
Posteriorの橙の破線は、Jeffreys事前分布の事後分布で計算したP値函数の類似物。定義についてはソースファイルを参照。
nbviewer.jupyter.org/gist/genkuroki…
にあります。
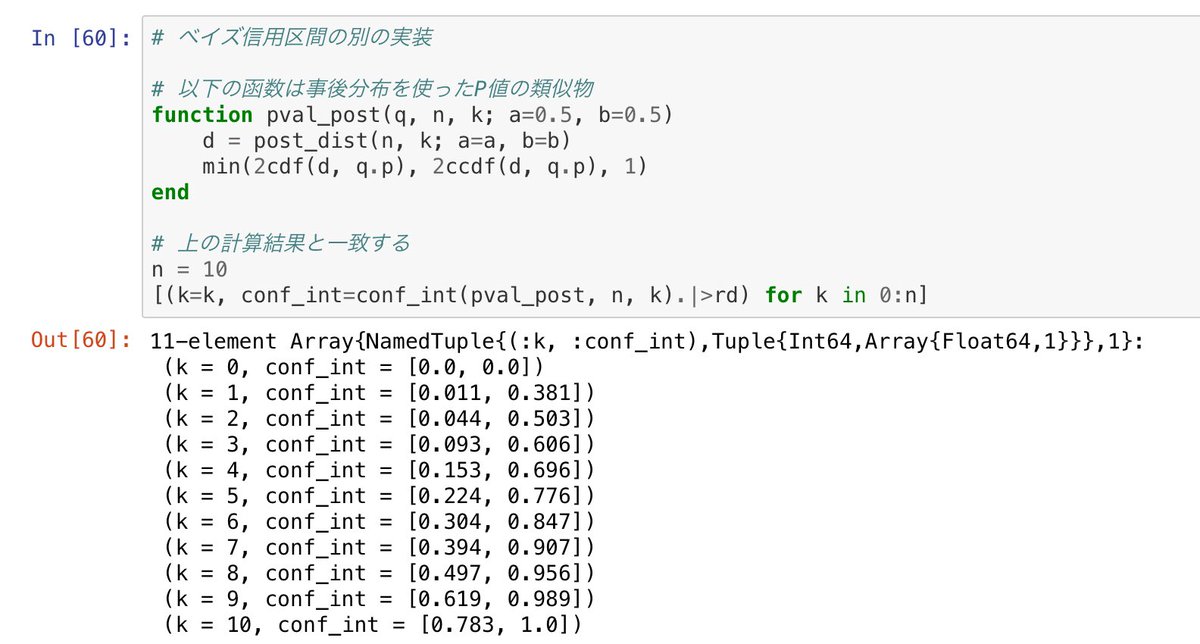
事後分布のCDFを F(θ) と書くとき、P値函数の類似物 pval_post(θ) を
pval_post(θ) = min{2F(θ), 2(1-F(θ)), 1}
と定義しています。両側検定のP値の類似物です。
これが通常のP値にほぼ一致。
そういう弱い人達をターゲットにして騙すための本にも見える。
豊田秀樹さんがやっているのはそういうこと。
騙されずにみんなで批判しないとトンデモ側が普及してしまう。
リンク先動画は、正規分布モデルの尤度函数をそのまま正規化して確率密度函数にしたものに従う「乱数」を生成する動画になっています。
須山敦志『ベイズ推論による機械学習』p.80のPlots.jlによる再現!
nbviewer.jupyter.org/gist/genkuroki…
Bernoulli分布モデル
も参照するといいかも。このノートブックは、渡辺澄夫『ベイズ統計の理論と方法』の話+α (AIC, WAIC, LOOCV, 自由エネルギー, WBIC)も含む。
ポイントは「真の分布がモデルで実現不可能な場合」も扱っているか否かです。
モデルp(y|x,w)によってq(y|x)=p(y|x,w₀)の形で実現できない真の分q(y|x)が実質的に出て来ているかで明瞭に判別できる。続く
y = sin x + noise, 0 ≦ x ≦ 2π
という法則で生成したデータと
y = M-1次の多項式 + noise
という多項式回帰モデルで作った予測分布を扱っています。このようにデータを生成した法則がモデルに含まれない場合も扱っています。
モデルは単なる道具であるという割り切りがあった方が、科学的に怪しげな言説を排除し易いと思う。
シンプルなモデルでは「頻度論」から「ベイズ」に移っても新しいことが出て来るわけではないです。
私が恐れていることは、「瀕死本」の類が沢山売れて、通常の仮説検定や信頼区間について誤解し、「ベイズ統計なら仮説が正しい確率が分かる」というデタラメを信じる人達が増えることです。
知的被害者が加害者側に回るループができるのが怖い。
ベイズ統計では、モデルの範囲内で真実に最も近い仮説Bが真実から程遠くても、ベイズ更新によって仮説Bが正しい確率はモデル内で100%に近付きます。
こういう類の確率を単に「仮説が正しい確率」と呼ぶのは詐欺だと思う。
真実とは違うモデル内での確率に過ぎない。
「瀕死本」的言説を全否定しながら、ベイズ統計の面白さを知ってもらえればうれしいです。
真のサイコロXでは3の目が出る確率だけが他よりほんの少し大きいだけなのに、ベイズ更新によってモデル内での「3,4の目が出る確率は1,2,5,6が出る確率の3倍である」という仮説の正しい確率は100%に収束しています。
これはベイズ統計での「事後確率」が持つ普遍的性質。
しかし、カンニングできない場合にウソを見抜くのは一般に非常に難しい。相手が無知ならウソを通し易くなります。
そういうことをやっちゃダメだと思います。
「瀕死本」の出版のタイミングで批判する人が増えるとよいと思います。
asakura.co.jp/books/isbn/978…
→ app.box.com/s/mju36d42ofg0…
の問題点の解説↓
nbviewer.jupyter.org/gist/genkuroki…
添付画像のケースでは、「ベイズ統計では仮説が正しい確率が分かる」という主張は「P値を仮説が正しい確率だと解釈してよい」と実質的に同じ意味になります。

nbviewer.jupyter.org/gist/genkuroki…
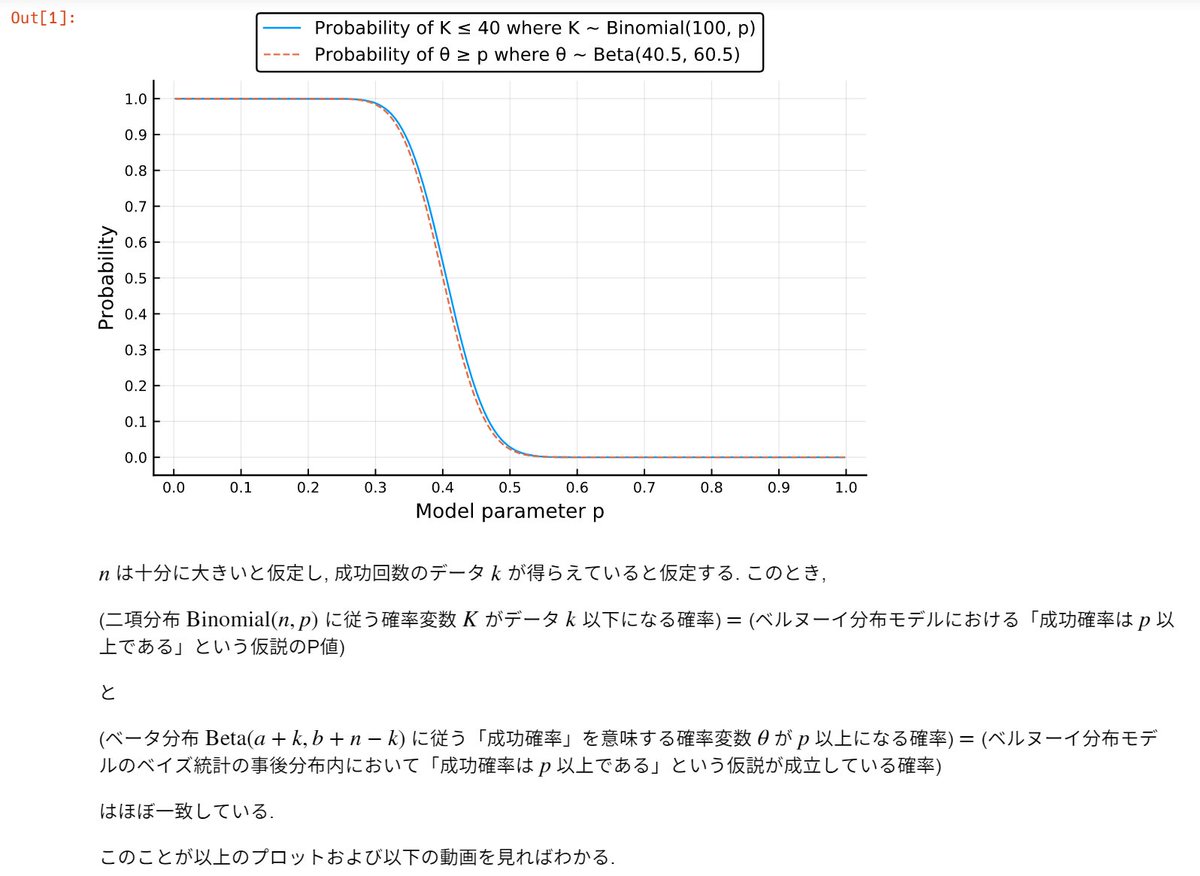
青の実線=ベルヌーイ分布モデルにおける「成功確率はp以上である」という仮説のP値
橙の破線=ベルヌーイ分布モデルのベイズ統計の事後分布内において「成功確率はp以上である」という仮説が成立している確率
これらはほぼ一致している。
これは非常によろしくないことだと思います。
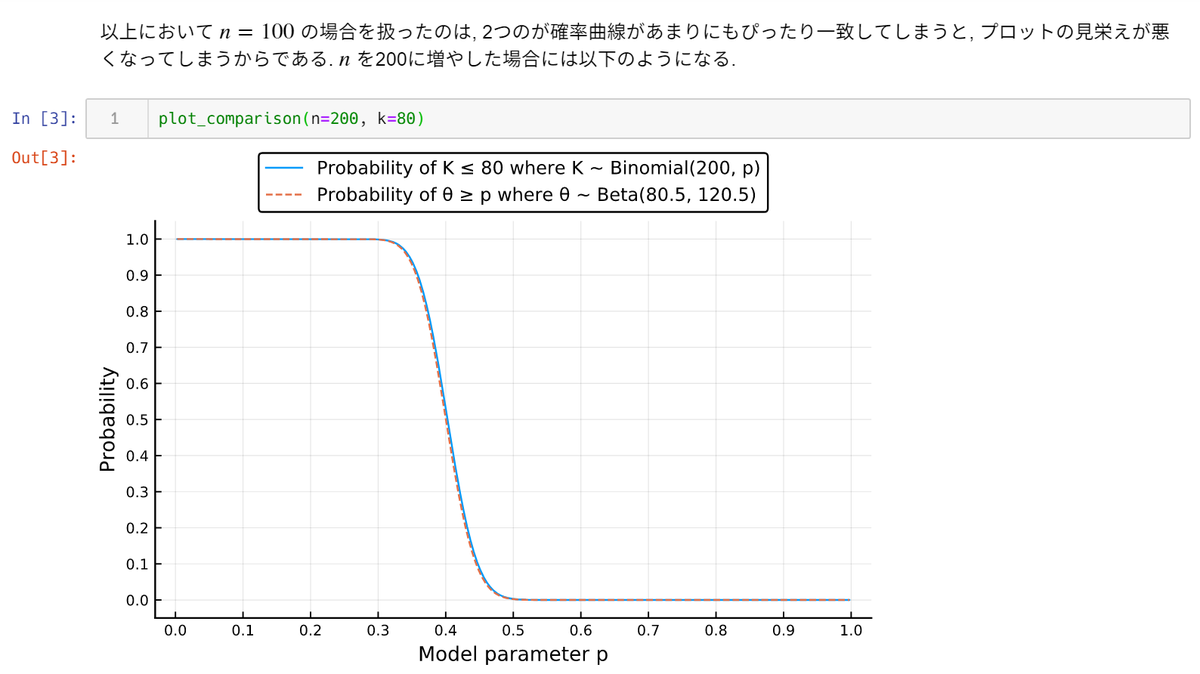
(1) 二項分布Binomial(n, p)に従う確率変数 K 対する K/n の分布の中心極限定理
と
(2) ベータ分布Beta(a+k, b+n-k)の中心極限定理
を比較してみるとよいです(中心極限定理=正規分布近似)。難しくないです。
nbviewer.jupyter.org/gist/genkuroki…
ベルヌーイ分布モデルにおける「頻度論」と「ベイズ」の比較
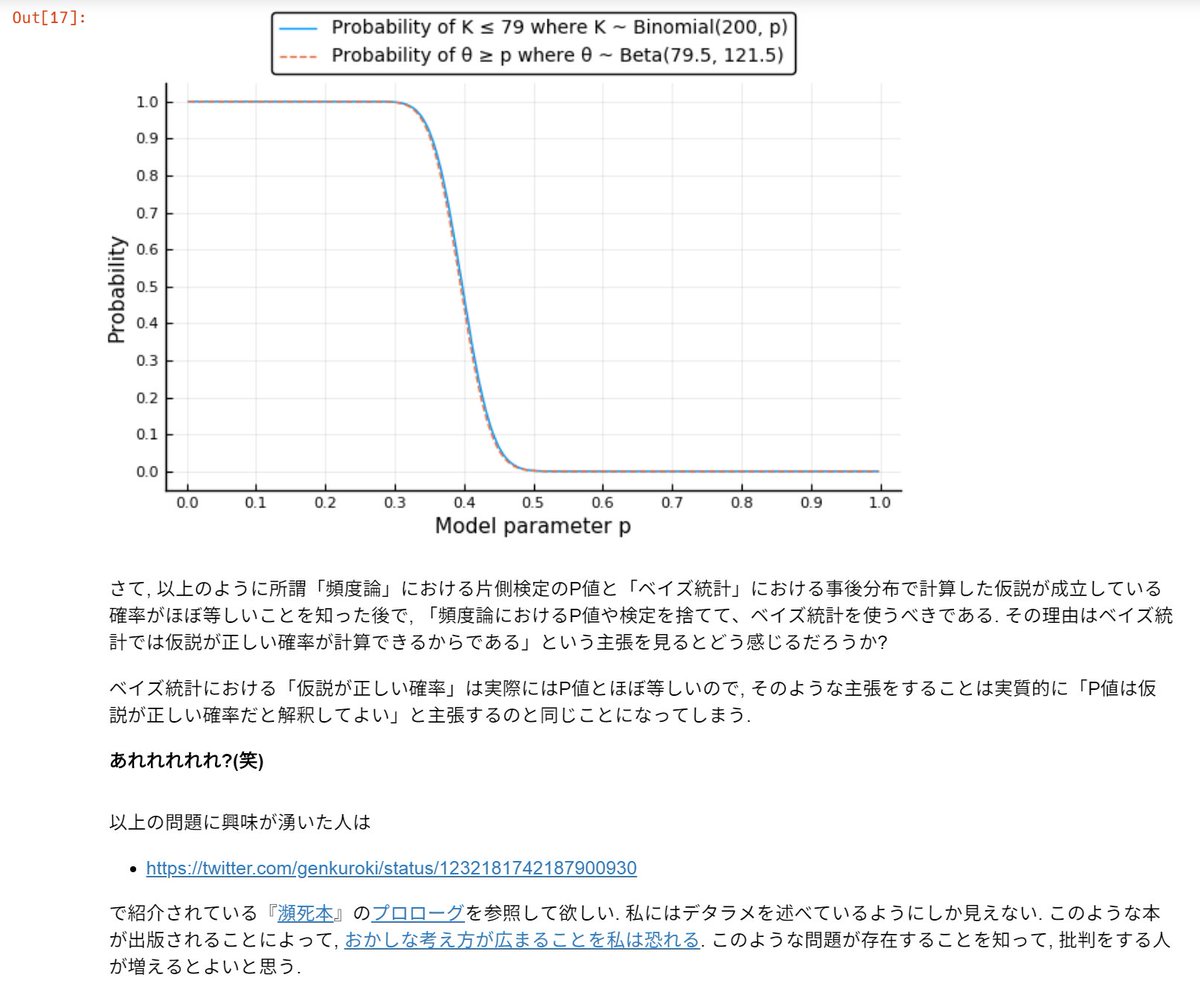

【p値と比較して phc (~)は, このような直観的な理解を与える指標です. しかも何回計算しても多重比較のような補正が必要ありません.】
ベイズ統計の事後確率なら多重比較の問題が起こらないと考えているようですが、「業界」ではそう信じられているのでしょうか?
だから、所謂「頻度論」で問題になることは、ベイズ統計でも問題になると考えられます。
豊田秀樹氏はそういう場合にもベイズ統計にすると頻度論ではできなかったことができると主張しているのでアウト。