Thread by @genkuroki

#統計 ベイズ統計の「主観確率」「ベイズ主義」「意思決定論」による解釈においては、主観確率のもとでの期待リスク最小化でベイズ統計における適切な推定法が特徴付けれます。

一見合理的なのですが、未知の法則の推測・予測を一切考えないことになっています。詳しく解説しましょう。

#統計 渡辺澄夫著『ベイズ統計の理論と方法』を読んでいる人のための解説にしたいので、その本の記号法に近いスタイルで説明します。(渡辺さんの本は「ベイズ主義」とは無関係)

まず、パラメータｗに関する事前分布φ(w)とパラメータwを持つ確率分布p(x|w)を用意します。

続く

#統計 「主観確率」の「ベイズ主義」においては、事前分布φ(w)は、ある人にとってのパラメータwに関する主観的な確信の度合いを表していると考えます。

例えば、その人が正しいパラメータの値がw=a付近である可能性が高いと思っていれば、事前分布φ(w)の値はw=aの近くで大きくなる。続く

#統計 そして、p(x|w)はその人が主観的に正しいと信じているモデルであると考えます。

より正確に言えば、データ X_1,X_2,…,X_n が従う確率分布の密度函数はあるパラメータwに関するp(x_1|w)…p(x_n|w) になっているとその人は主観的に信じていると仮定します。

#統計 さらに「意思決定論」では、以上の設定のもとでリスク函数を追加で与えて、その人は主観的な期待リスクを最小化するように意思決定を行うと考えます。

以上のように考えること自体が不合理なのではないことに注意。数学的には普通の話。続く

#統計 簡単な例として、データ X_1,…,X_n から得られるパラメータ w の推定値が f(X_1,…,X_n) の形で与えられるとし(函数 f をパラメーターの推定法と呼ぶ)、その人は自分の主観内で、推定値の二乗誤差

(w - f(X_1,…,X_n))²

の期待値を最小にするような推定法 f を選択する場合を考えましょう。

#統計 二乗誤差の主観的な期待値は、X_1,…,X_nの主観的標本分布とパラメータwの主観的事前分布に関する平均の形で書ける：

主観的期待二乗誤差
= ∫∫…∫ φ(w)p(x_1|w)…p(x_n|w) (w - f(x_1,…,x_n))² dx_1…dx_n dw

これを最小化する推定法fが「意思決定論」の解の例になっているわけです。続く

#統計 実際にそれを計算すると、主観的期待二乗誤差を最小化する推定法 f はベイズ統計におけるパラメータの事後分布における期待値になることが、そう難しくない議論でわかります。

続く

#統計 具体的に式で書くと、主観的期待二乗誤差を最小にする推定法 f は次の形になります：

f(X_1,…,X_n) = ∫ φ*(w|X_1,…,X_n) w dw.

ここで、φ*(w|X_1,…,X_n)は事後分布です：

φ*(w|X_1,…,X_n) = φ(w)p(X_1|w)…p(X_n|w)/(分子のwに関する積分).

続く

#統計 以上によって、「主観確率」「ベイズ主義」「意思決定論」の枠組みにおいて、自分の主観のもとでの期待二乗誤差を最小化するような推定法を選択する人は、推定法として事後分布の期待値を採用することがわかりました。

続く

#統計 同様に、「主観確率」「ベイズ主義」「意思決定論」の枠組みにおいて、自分の主観のもとでの期待汎化誤差を最小化するような予測分布を選択する人は、予測分布として「パラメータwに関する事後分布によるp(x|w)の平均」(ベイズ法のいつもの予測分布)を採用することも示せます。

#統計 データX_1,…,X_nから作った予測分布を r(x|X_1,…,X_n) と書くとき、その主観的な期待汎化誤差は

-∫∫…∫∫ φ(w)p(x_1|w)…p(x_n|w)p(x|w) log r(x|x_1,…,x_n) dx_1…dx_n dx dw

と表されます。これを最小化する r(x|x_1,…,x_n) は p(x|w) の事後分布関する平均になります。

#統計 以上のような話を数学に慣れていない人が聞くと、期待二乗誤差や期待汎化誤差を最小化するようにパラメータの推定法や予測分布の作り方を決めているのだから、「なんて合理的な考え方なのでしょうか！」と思ってしまうかもしれません。

#統計 しかし、以上のストーリーに渡辺澄夫著『ベイズ統計の理論と方法』では q(x) と書かれている「真の分布」が一切登場していないことに注意して下さい！

ここが最も重要なポイントです。

#統計 「主観確率」「ベイズ主義」「意思決定論」の枠組みによるベイズ統計の解釈においては、期待リスクが φ(w) と p(x|w) のみで記述されるモデル内部の言葉で定義されており、モデル内部の設定で期待リスクを最小化しているだけだということに気付く必要があります。

#統計 「主観確率」「ベイズ主義」「意思決定論」のベイズ統計においては、未知の真の分布 q(x) の予測に関する汎化誤差を考えることはなく、主観的に構成されたモデル内部における φ(w) と p(x|w) のみを用いて記述される主観的期待汎化誤差を最小化しているだけなのです。

続く

#統計 「主観的期待リスク最小化」は「合理性」の定式化としてよく使われているおなじみのものです。

しかし、それでベイズ統計を解釈してしまうと、「未知の分布が生成していると想定されるデータを用いて、未知の分布に関する推測や予測を行う」という統計学の重要な側面が失われてしまうのだ！

#統計 ベイズ統計を「主観確率」で解釈して、「主観的な期待リスク最小化」(リスクとして主観内での二乗誤差や主観内での汎化誤差を考える)について説明すること自体は数学的に十分に合理的な行為です。

しかし、推測統計学の重要な側面が失われることについて正直に説明しないのは非常にまずい！

#統計

①未知の分布に関する推測や予測のみが統計学の内容である

と考えるのは__誤り__です。しかし、

②未知の分布に関する推測や予測を完全に捨ててしまっては、統計学の名に値しなくなってしまう

と考えることは穏当でしょう。

穏当な主張である②を①だと誤解して触れ回る行為は悪質注意！

#統計 このスレッドでは私自身が「主観確率」「ベイズ主義」「意思決定論」の枠組みにおけるベイズ統計の解釈について解説しています。

しかし、その解釈では、未知の分布の推測・予測という統計学の重要な側面が失われてしまうことについても正直に説明しないと非常にまずい。

正直さの問題。

どーでもいーことですが、気になったので訂正。

✖主観確率のもとでの期待リスク最小化でベイズ統計における適切な推定法が特徴付けれます

〇主観確率のもとでの期待リスク最小化でベイズ統計における適切な推定法が特徴付けられます

「ら」が抜けた。

https://twitter.com/genkuroki/status/1324448226477400064

スレッド間相互リンク

https://twitter.com/genkuroki/status/1324448879081713664

#統計 「主観的期待リスク最小化」によるベイズ統計の解釈は入門的解説では結構定番のものです。

数学的内容を解説してくれること自体は良いことですが、その解釈では主観内での期待リスクを最小化するだけで、主観の外にある未知の分布の推測・予測を扱えなくなることも最初に強調しておくべき。

#統計 実際に「主観的期待リスク最小化」によるベイズ統計の解釈が結構定番であることは

ai-trend.jp/basic-study/ba…

の添付画像の部分を参照しても分かると思います。

現実の未知の法則の推測をすることを一切考えずに純粋に主観的な平均リスクを最小化する(笑)

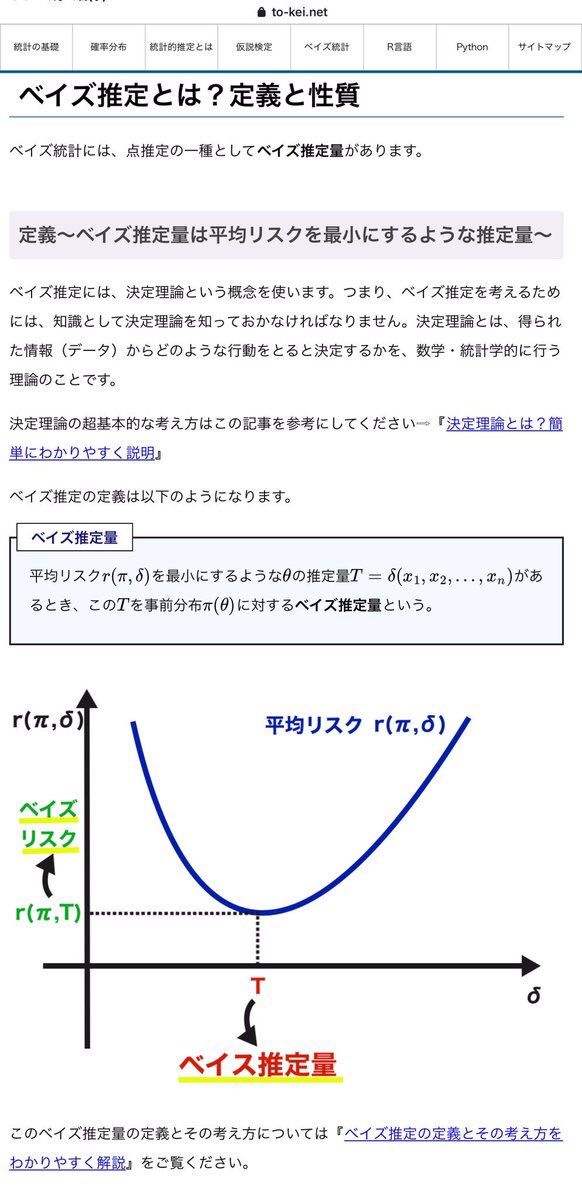
#統計 他にも、定番の教科書の1つである久保川達也著『現代数理統計学の基礎』のサポートページ sites.google.com/site/ktatsuya7… の添付画像の部分も参照してください。

事後分布の期待値や条件付き確率分布としての標準的なベイズ版の予測分布はモデル内での期待リスク最小化で特徴付けられる。

#統計 そのような教科書的解説で定番の期待リスク最小化は「よく知られているものの特徴付け」に過ぎず、数学に詳しければもっと一般的な視点から理解可能なものです。

わけのわからない現実に立ち向かうための道具にはなりません。

#統計 例えばベイズ統計と無関係に、確率変数Xについての期待二乗誤差 E[(X - m)²] を最小化する m はXの期待値 E[X] になります。条件付き確率分布も同様な特徴付けがある。数学的には基本的。

しかし、それを「主観内期待リスク最小化」に応用しても現実の未知の法則の推測には役に立たない。

#統計 現実の未知の法則の推測の問題についてはひとまず無視して、主観的に作ったモデル内でどうするのがベストであるかを考えるとどうなるかを数学的に分析することはどんどんやればよい。

しかし対外的な解説を書くときには、現実の未知の法則の推測の問題を無視していることも正直に言うべき。