Thread by @pbeltranp

La multiplicación de fracciones. Unpacked.

Lo voy a contar desde el modelo de medida. Y voy a empezar por la multiplicación de un número natural por una fracción, donde esta representa una cantidad de magnitud.

De esta manera, esta operación responde a enunciados donde se agregan cantidades de magnitud. Por ejemplo, 5 botellas de 4/3 de litro.

Ese 4/3 u son 4 subunidades de tamaño 1/3 u. En este caso hablamos de cuatro tercios de litro. Sí, vale, sé que sois mayores y os podéis inventar un enunciado más contextualizado. Como son 5 botellas, podría hacer 4/3+4/3+4/3+4/3+4/3.

Al fin y al cabo, ¿cuántas subunidades tendría ahora? Efectivamente, 5 veces 4 subunidades de tamaño 1/3 u son 20 subunidades de tamaño 1/3 u. En resumen, veinte tercios. Vamos a hacerlo gráficamente de manera que este discurso se alinee con los gráficos.

Primero representamos la unidad de medida (nuestra u, que en el ejemplo es un litro).

Pablo, has dibujado un rectángulo. Sin regla ni nada. Te habrás quedado ancho, ¿no? Pues es que es fundamental empezar representando la cantidad de magnitud, y para ello tiene que quedar clara cuál es la unidad de medida.

Seguimos. Como en el ejemplo estamos hablando de tercios de unidad, dividido la unidad en tres partes iguales.

Y luego, añado el tercio que me falta para hacer 4/3 u. Es decir, mis 4/3 de litro del ejemplo.

Ahora ya solo tengo que hacer 5 de estos. Y ya tengo unos gráficos que se alinean con lo que he dicho antes. ¿Cuántas subunidades hay ahí? ¿De qué tamaño? Efectivamente, 20 de tamaño 1/3u. 20/3 u.
Pd. Sí, me he salido de la «pizarra» 🤦🏻‍♂️

He utilizado una fracción «impropia» para ilustrar que, mediante el significado de medida, aparecen de forma natural. Si me seguís, sabréis que no me gusta insultar a las fracciones con peyorativos de este calibre. Pobrecitas.

¿Acaso nos ha hecho falta poner un «partido por uno» para hacer esto? Pero es que ese uno es una ayuda...
Una ayuda, ¿para qué exactamente?

Vamos con la división de una fracción por un número natural. Porque nos va a hacer falta antes de ir a la multiplicación de fracciones. Responde a enunciados del tipo «tenemos 4/3 de litro de agua y la repartimos de forma equitativa en 6 vasos, ¿cuánta agua toca en cada vaso?»

Si habéis estado atentos, ya sabéis cómo representar 4/3 de litro. Un método consiste en dividir cada subunidad en 6, cosa que se ilustra en este dibujo y que se corresponde con estas operaciones. ¿Qué tamaño tiene ese rectangulito gris?

Efectivamente, 1/18 u. Y aquí radica la importancia de tener clara cuál es la unidad de medida. ¿Alguien había pensado 1/24 u?

Finalmente, solo queda coger 4 de esos 1/18 u.

Segundo método. ¿Se podría haber hecho sin pasar por los dieciochoavos? No te hagas spoiler y piénsalo.

En el primer método hemos dividido el tamaño de subunidad por 6, de forma que a cada uno le tocan 4 de esos nuevos trocitos. Pero podíamos haber tratado de repartir el número de subunidades. No podemos repartir 4 subunidades de forma entera entre 6, así que amplifico.

Así tengo expresada la misma cantidad de magnitud en novenos. Y claro, 12 novenos sí que puedo repartirlos entre 6. Tocan a 2 novenos.

Cuando multiplicamos dos fracciones, pensando desde el modelo de medida, estas pueden tener dos significados: como operador y como cantidad de magnitud.

Caso 1. Una de ellas actúa como operador. Responde a enunciados del tipo «nos hemos comido 3/2 de 5/4 de kg de merluza, ¿cuánta merluza hemos comido?». El 3/2 es operador y el 5/4 es cantidad de magnitud.

El resultado va a ser otra cantidad de la misma magnitud que el 5/4. En este caso, masa o peso. Vamos a resolverlo de forma gráfica. Me salto los pasos que ya conocéis y represento los 5/4kg.

Mostraré a la vez el discurso aritmético y el gráfico. Igual que antes, hay dos maneras de hacerlo.
[TO BE CONTINUED]

El operador puede actuar primero disminuyendo y luego aumentando, o al revés. Pensemos en nuestro 3/2. Puedo disminuir dos veces la cantidad inicial y luego aumentarla tres veces (hacer la mitad y triplicar)

Represento la unidad (que resalto en verde fosfi), después construyo el 5/4 kg, y lo divido por la mitad. ¿Qué tamaño tiene el rectangulito gris? Recuerdo: son subunidades de kg.

Eso es, se trata de octavos de kg. Solo falta triplicar esa cantidad para construir el 3/2 de 5/4 kg. ¿Qué cantidad representa? 15 subunidades de tamaño 1/8 de kg. 15/8 kg.

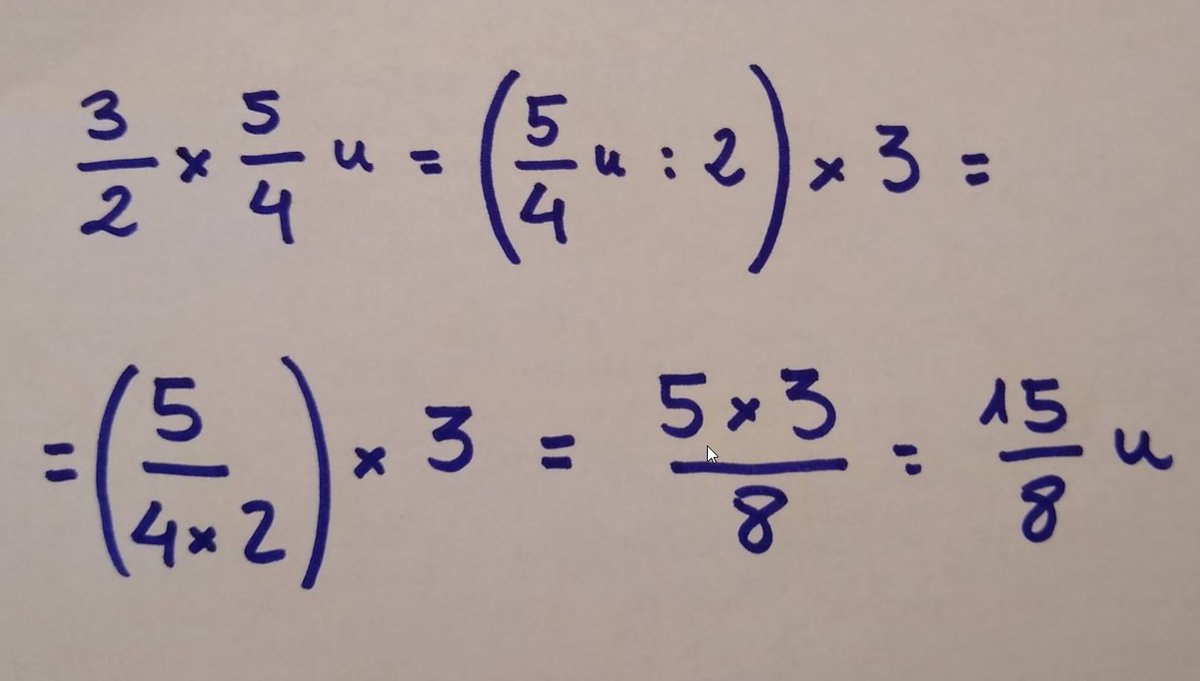
La segunda manera consiste en aumentar tres veces la cantidad inicial y luego disminuirla dos veces (triplicar y luego hacer la mitad). La triplico.

Y luego la divido entre dos. Aquí tengo dos opciones, por la línea de puntos o a lo largo, relacionándose cada una de las opciones con lo que he comentado antes al dividir una fracción por un número natural.

No hay muchos applets que aborden esto desde la medida. Casi todos lo hacen desde el parte-todo, que para esto tiene limitaciones evidentes (¿hola impropias?). Os dejo el que preparó en GeoGebra nuestro compañero de @FacultadEducaUZ Alberto Arnal.
geogebra.org/m/PVdO6bj8

Pero, ¿qué ocurre cuando multiplicamos dos fracciones en las que ambas son cantidades de magnitud? Pues que el resultado será una cantidad de OTRA magnitud. Por ejemplo, «cuál es el área de un rectángulo de lados 3/2m y 5/4 m».

Me empiezo representando esas cantidades de longitud. Esto es el 5/4 m.

Y esto es el 5/4 m y el 3/2 m.

El rectángulo de lados 5/4 m y 3/2 m, con la unidad de medida en que quiero expresar su área (metro cuadrado).

¿Cuánto miden cada uno de esos rectangulines? ¿En cuántos ha quedado dividida la unidad de área? ¿Cuántos de esos he tenido que usar para recubrir el rectángulo original?

Ahí tenéis el 15/8 de metro cuadrado. Necesito 15 subunidades de tamaño un octavo de metro cuadrado.

La división de fracciones es algo más compleja. Sin embargo, y a pesar de que el campo de problemas aumenta, aquí en el hilo están los elementos necesarios. Nos emplazamos para otro momento.

Eso sí, trabajar el significado de medida no es llegar y pum. Hay que articular todo un discurso basado en ciertas acciones físicas con diferentes magnitudes.

Y otro día puedo contar lo mismo desde el significado de reparto. En fin, cosas tontas que se ven en las facultades de educación. Aprovecho para etiquetar esto con #cosicasdeDAII, a modo de síntesis para el alumnado de @FacultadEducaUZ

Si quieres más lectura sobre esto de la medida y las fracciones para la merienda o el desayuno de mañana...

https://twitter.com/pbeltranp/status/1195981853985038336

Recursos interesantes sobre medida: los materiales que prepararon @SergioMJGR y @auroradp64 para trabajar las fracciones desde el modelo de medida en ESO (adaptable a Primaria, claro).

https://twitter.com/SergioMJGR/status/1233098195720380416

Y sobre medida directa de áreas:

https://twitter.com/SergioMJGR/status/1233139726875611138?s=08

Aclaración. En el de la merluza he hecho 3/2 x 5/4 kg, buscando que sean ambas impropias, que es el caso más llamativo. Pensemos que van en paquetes de 5/4 kg y que nos hemos comido tres medios.