Thread by @pbeltranp

La división de fracciones. Unpacked.

Parece que solo hay dos opciones de «dar» o «ver» esto. Una, como el producto cruzado; otra, multiplicando por la inversa.

¡Mucho mejor lo de la inversa! Claro, te aprendes la regla de la multiplicación de fracciones, y dividir es lo mismo dando la vuelta a una de ellas.

¡Pero yo prefiero la otra! Es como cuando miro si las dos fracciones son iguales, que se hace el producto cruzado. Déjate de inversas, ¿qué es eso de invertir?

He puesto comillas en dar y ver. Esto ni se da ni se ve, se hace, y mientras se hace, se reflexiona y se le da significado. De lo contrario, para ponernos a aplicar una regla que es magia, hay un atajo excelente que se llama calculadora.

Vamos a la faena. Aviso que conceptualmente es más complicado que el de la multiplicación. Por eso, sugiero haber visto este hilo antes de seguir, pero esto es como elige tu propia aventura.

https://twitter.com/pbeltranp/status/1332631071553425410

Caso en que dos fracciones que representan cantidades de magnitud y que multiplicadas dan una cantidad de una nueva magnitud. Por ejemplo, el área de un rectángulo conocidos los lados (multiplico los lados, longitudes, para hallar el área).

Entonces, si conocemos el área y uno de los lados, veríamos que tenemos que dividir. Un ejemplo con números enteros: «Un rectángulo tiene área 15 u2 y uno de sus lados mide 5 u, ¿cuánto mide el otro?» Lo que sea, pero multiplicado por 5 tiene que dar 15.

Aquí, por tanto, la división tiene sentido combinatorio. Con fracciones: «Si tenemos un rectángulo de área 3/4 m2 y uno de los lados mide 7/5 m, ¿cuánto mide el otro?» Observemos que ahora nuestras unidades son metros y metros cuadrados (en genérico, antes las he llamado u y u2).

¿Tiene sentido aquí pensar en cuántas veces cabe el 7/5 en 3/4? ¿Tiene sentido aquí pensar en multiplicar la una por la inversa de la otra? ¿Qué significaría en este contexto 5/7m^-1 o 4/3 m^-2? 🤷🏻‍♂️

Me construyo el lado conocido (7/5 m). He elegido una fracción impropia (pobrecitas) para que quede claro cómo se construyen. Comienzo con la unidad.

La divido en 5 partes iguales para tener quintos de metro.

Y añado dos más para tener los 7/5 m.

Me construyo un rectángulo de área 3/4 m2. Para ello, primero me construyo la unidad de área, el metro cuadrado.

Lo divido en cuatro para tener cuartos de metro cuadrado, y tres de ellas serán los tres cuartos de metro cuadrado. En rojo, a la derecha, he comenzado a dibujar el lado desconocido.

Esa misma área, la puedo expresar en veinteavos de metro cuadrado.

Y ahora lo que voy a hacer es recomponer ese área de 3/4 de metro cuadrado para formar un rectángulo que tenga como lado 7/5 de metro. Puedo mover cuatro de los veinteavos de metro cuadrado así, y me queda el azulito.

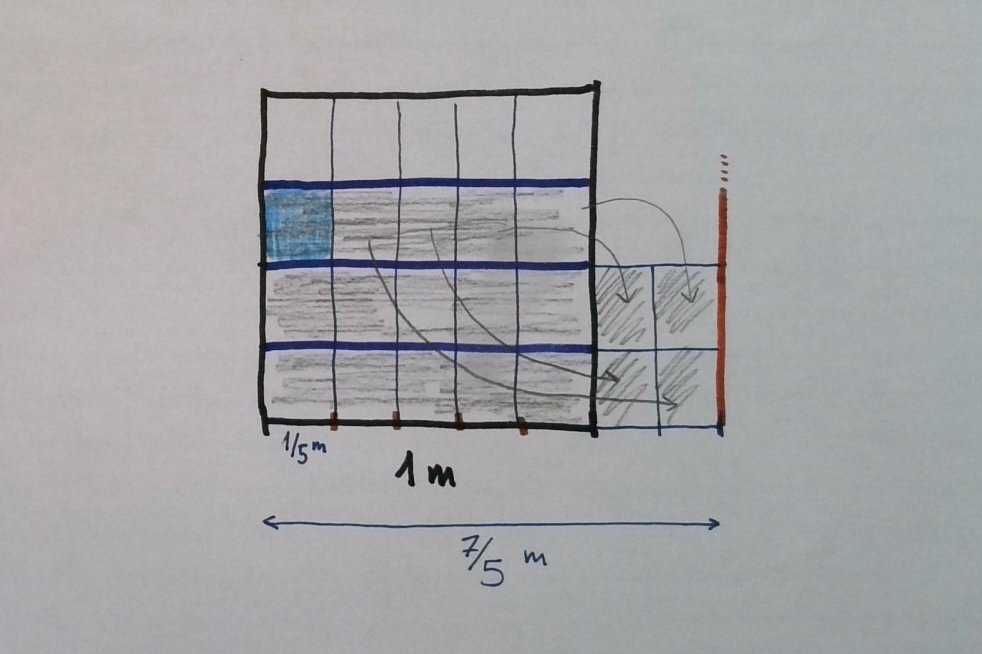
Tendré que repartir ese azulito a lo largo de todo el "ancho" del rectángulo. Por lo tanto, lo tengo que dividir en 7. Observemos las divisiones en el lado desconocido.

Y ya hemos resuelto el problema. El lado desconocido mide 15/28 m (7/28 + 7/28 +1/28). Esto responde a:
3/4 m2 : 7/5 m = 15/28 m

El denominador del resultado, 4x7, representa las subdivisiones que hemos tenido que hacer en el lado desconocido que queremos medir. Cada subunidad inicial, 1/4 m, se ha subdividido en 7 partes iguales, lo que da lugar a subunidades de tamaño 1/28 m.

El numerador, 3x5, se obtiene al buscar cuántas de estas subunidades de tamaño 1/28 deben aparecer en el lado buscado. Le acabamos de dar significado a la regla del producto cruzado para la división.

¿Vamos a por otro? Recordemos el caso de la multiplicación de fracciones, en que una fracción representa una cantidad de magnitud y la otra es un operador que la modifica. Ejemplo: «Hemos comprado 3/4 de 7/5 kg de harina».

Para hacer 3/4 de 7/5 kg ya vimos en el de la multiplicación que podíamos dividir primero entre cuatro y luego triplicar (tres cuartos de...) o triplicar primero y dividir luego entre cuatro (un cuarto del triple de...). En cualquier caso, 21/20 kg.

¿Qué ocurre si a 21/20 kg le aplico el operador inverso?
Es decir, si antes he dividido entre 4 y luego he triplicado, ¿qué pasa si divido entre 3 los 21/20 kg y luego los cuadruplico?

Efectivamente, se obtiene la cantidad inicial. Aplicar el operador inverso (4/3 en lugar de 3/4) es lo mismo que, en sentido combinatorio, dividir los 21/20 kg entre la fracción del operador inicial. [To be continued]

Lo de antes podría responder a un enunciado de este tipo: «Hemos comprado 3/4 de un saquete de harina, y al irlo a pesar eso eran 21/20 kg. ¿Cuánto pesaba el saquete de harina».

Bueno pues si el saquete lo hemos dividido en cuartos y hemos cogido tres, ahora hago tercios de la cantidad que tengo y tomo cuatro. Le hemos dado sentido al operador inverso. Nótese que en el ejemplo del rectángulo no podíamos dar sentido a la fracción inversa.

Incido en el uso de magnitudes continuas porque todo esto con magnitudes discretas no tendría sentido. Se ha de poder fraccionar todo lo que queramos. Si hablamos de bolis, vacas o cualquier otro objeto no fraccionable (y hablo de vacas vivas), no tiene sentido la división.

Seguimos, que esto todavía no ha acabado. Tampoco voy a abordar exhaustivamente todo lo que quedaría, pero recuperemos la idea de división. La división no siempre indica reparto. Su significado como agrupamiento es algo que suele pasarse por alto. ¿Qué diferencia hay?

Comparad los enunciados «Tenemos 15 tortas y queremos repartirlas entre 5 personas, ¿cuántas tocan a cada una?» y «Tenemos 15 tortas y quiero hacer paquetes de 5 tortas. ¿Cuántos paquetes podré hacer?»

Efectivamente, ambos son 15:5, pero en el primero hacemos una división con significado de reparto (3 tortas por persona), mientras que el segundo es con significado de agrupación (3 paquetes de 5 tortas).

Vamos con las fracciones. Consideremos el contexto de las tortas (el gastronómico, no el pugilístico): «Tenemos una torta de 1/2 kg y quiero hacer trozos de 1/8 de kg. ¿Cuántos trozos podré hacer?»

Conecta con el significado de agrupamiento, ya que puede interpretarse como «¿Cuántos grupos de 1/8 kg puedo hacer con 1/2 kg?». Pero también con la medida: «Tengo una cantidad de 1/2 kg (expresada en fracciones de kg) y quiero medirla en porciones (nueva unidad) de 1/8 kg».

Sí, enlaza con la idea de «ver cuántas veces cabe el 1/8 en 1/2». Pero ojo, si lo hubiese planteado al revés, qué. ¿Cómo daría sentido a ver cuántas veces cabe el 1/2 en 1/8? La medida, de nuevo, permite abordar esto, porque simplemente se trataría de medir 1/8u con 1/2u. Es 1/4.

Es normal que el alumnado no perciba las fracciones como números. Trabajar las fracciones priorizando el parte-todo conlleva este y otros obstáculos. El modelo de medida, con las fracciones representando cantidades de magnitud, incide en las propiedades de los racionales.

Nos dejamos para otra ocasión el significado de razón, que también permitiría abordar la división de fracciones.

Como siempre, para ampliar. Sobre los obstáculos del parte-todo:

https://twitter.com/pbeltranp/status/1195981853985038336

Y decir que estas cositas vienen abordadas de forma exhaustiva en el «Números y algoritmos» de Gairín y Sancho @edsintesis.

Me dejo guardado aquí el applet de @alegallardo28, que puede dar mucho juego si se discute lo que ocurre en torno a la medida.

https://twitter.com/alegallardo28/status/1335508769724375040