Thread by @genkuroki

#統計 リンク先スレッドでは仮説「表が出る確率は0.5以上」という仮説について「止め方の違い」を扱いました。

今度は、「表の出る確率の推定」について「止め方の違い」を扱ってみました。

gist.github.com/genkuroki/20c0…

https://twitter.com/genkuroki/status/1339313220784287746

#統計 続き。最適な事前分布として Beta(a, a) の形のものを探しました。n=12, k=3の場合を扱う。真の分布での表の出る確率はq=0.005:0.005:1を動かした。

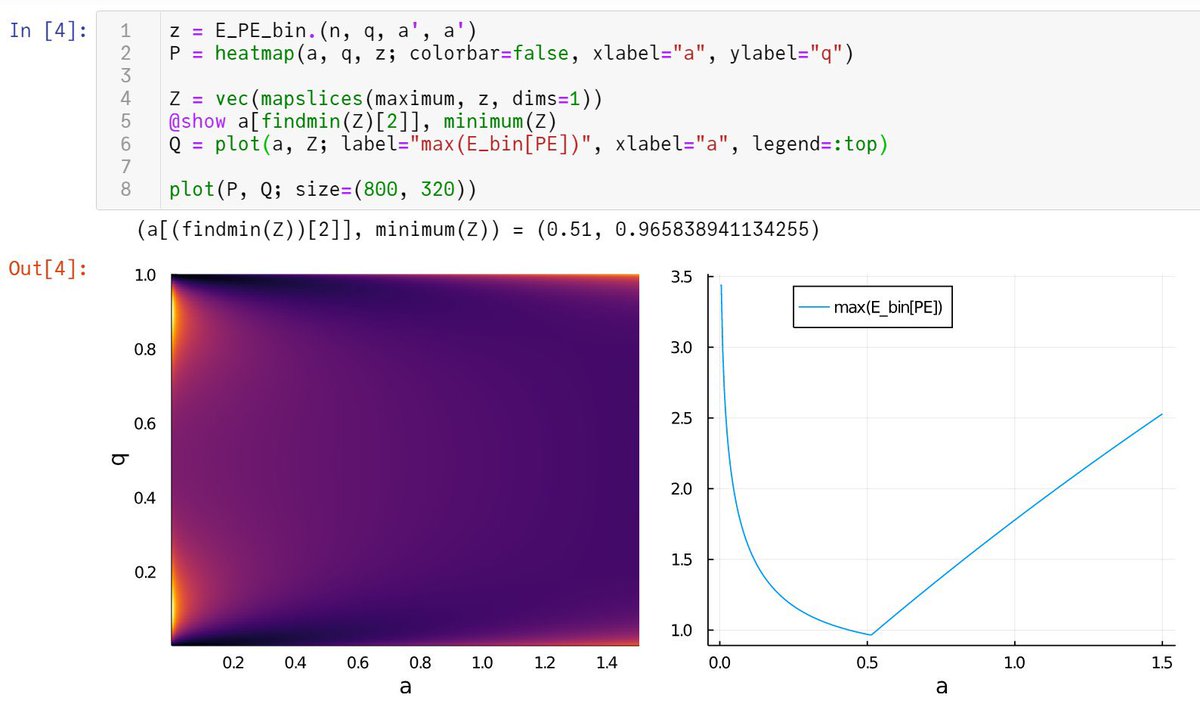
二項分布モデル(試行回数n=12を固定)の場合には、qを動かしたときの期待予測誤差の最大値を最も小さくするaの値は0.51だと計算できました。

#統計 雑な計算なので、二項分布モデルの場合には、おそらく本当は a=1/2 のJeffreys事前分布を使うのがよいということなのだと思います。

#統計 この計算はちょっと自信がないのですが(バグを発見したら教えて下さい)、負の二項分布モデル(ちょうどk=3回表が出るまで試行し続ける場合)では、a=0.37の場合がよさそうだというような計算結果が得られました。

しかし、右側のグラフを見ると、a=0.5の場合と最大予測誤差はそう変わらない。

#統計 負の二項分布モデルの場合の計算についてはまだ自信が持てていません(バグを見付けたり、同結果を再現できた人がいたら教えて下さい)。

しかし、データの取得法によって、データの真の分布の想定は変わるので、期待予測誤差の定義も変わり、最適な事前分布の定義も変わります。

#統計 最初に試行回数nを固定した場合の実験結果のデータを使った場合と、表がちょうどk回出るまで試行し続けた実験結果のデータを使った場合で、期待予測誤差の定義は変わり、最適な事前分布の定義も変わります。

事前分布をリスク制御のために使うときにはこのように考えなければいけません。

#統計 補足：この場合に、ベイズ法の予測誤差はデータと表が出る確率の真の値だけで決まり、「止め方」によらない。しかし、そのデータの確率的揺らぎに関する期待値の計算では、「止め方」によって変わるデータの分布を使うので、期待予測誤差の定義は「止め方」ごとに違うものになります。

#統計 一般に、尤度函数が(定数倍の非本質的違いを除いて)等しくても、データの取得の仕方によって、推定が外れるリスクは変化します。(こういうことは皆さんの方が詳しいでしょう。)

この点を見逃して、尤度函数が(定数倍を除いて)等しければ「同じ証拠が得られたことになる」と考えるのは誤り。

#統計 再掲: データの分布がn=12の二項分布の場合

a>0のa→0の極限が最尤法に対応しています。

期待予測誤差のヒートマップ(添付画像左側)を見ると、aが0付近ではq=0.1, 0.9付近で期待リスクが高めになっています。事前分布を使うとそれを緩めることができるわけです。

#統計 補足：「n回中表がk回」のデータから得られる事前分布Beta(a,a) (a>0)のベイズ予測分布は「表の出る確率は(k+a)/(n+2a)」になります。(k+a)/(n+2a)は分布Beta(k+a, n-k+a)の期待値。

最尤法の予測は「表の出る確率はk/n」になります。

このスレッドでは扱っている場合はこんな感じで易しい。

#統計 こうやって詳細については書いているのは、もしも私がアホなことをやっていたら(よくある)、見つけ易くするため。

ダメなやつは論争になると自分の発言に間違いを見つけ難くする。議論の帰結よりもそういうことの方が不快だといつも思っているので、心配になって詳細を説明したくなる。

#統計 ベルヌイ試行の統計学についてウルトラ精密なことを言っても実用的には意味がないと思っています(√nを計算する人になりたい)。

しかし、最も易しいトイモデルとしての教育的価値は高い。このスレッドでは事前分布を適切に決めれば最大期待予測誤差を下げられる場合があること示したつもり。

#統計 統計学は【お墨付き】を得るための道具ではなく、ギャンブルでの勝ち目を増やすための道具です。そのためには、ギャンブルで生じるリスクを分析することが必須。

未知の真の分布に基くデータの分布の理論的想定はリスクの分析のための基本的な道具。事前分布はリスクを下げるために使える。

#統計 このスレッドにおける事前分布は「主観確率の表現」に全然なっていないことに注意。「主観」という用語の曖昧さを利用すれば「主観確率の表現」と言えるのですが、そういう詭弁まがいのことを言うのは時間の無駄。

事前分布はリスクを下げるための道具として使われています。

#統計 事前情報をもとに偏った事前分布を採用することをこのスレッドの議論が否定していないことに注意(肯定もしていない)。

事前情報をもとに偏った事前分布を採用した場合には、その合理性について別の前提や証拠が必要になります。それだけの話。

#統計 事前分布に限らず、どのような数学的道具であろうと、状況と目的に合わせて合理的な使い方であるとみなせる証拠を示せるなら自由に使ってよい。

合理的とみなせる理由はまともであれば何でも良い。

もちろん、既存の陳腐な主義を梃子の支点とするような「正当化」はまともだとみなされない。

#統計 まともだとみなされない既存の陳腐な主義には、主観的ベイズ 主義、尤度原理に基く尤度主義などがある。あと、戯画化された頻度主義もまともとみなされるべきではない。

いちから全部考え直して得られた穏健でまともな主義とそれらは異なる。

#統計 こういう言い方をしなければいけない理由は、「主義による統計学はダメだ」と言うときの「主義」については具体的な主義を想定していることが文脈的に明瞭であるのに、曖昧に主義一般と解釈しておバカなことを言い出す人達をよく見かけるからである。

#統計 補足：予測誤差 PE はKullback-Leibler情報量で定義していますが、添付のグラフの右側の縦軸のスケールは2n倍した値になっています。

KL情報量の2n倍を予測誤差PEの定義としています。

2n倍するとχ²分布のスケールになる点が便利です。

私はこのスケールを多用しています。

#統計 そのスケールで期待予測誤差E[PE]はn→∞で1に収束します。1はモデルのパラメータの個数。

最大期待予測誤差を1に抑えるには事前分布としてJeffreys事前分布を採用すれば良さそうということをグラフは示しています。

警告：特異モデルでJeffreys事前分布は予測誤差を悪化させる。

#統計 関連

https://twitter.com/genkuroki/status/1339613121376256003

#統計 実験の止め方ごとに最大期待予測誤差を最小にするBeta(a, a)型共役事前分布を求める計算を少し拡充しました。n=12, k=3 の場合だけではなく、n=120, k=51の場合も追加しました。n, kをそのように大きくしたら、二項分布モデルもで負の二項分布モデルでもJeffreys事前分布が最適のようです。

#統計 アニメーションを作りました。

とても分かり易い！

データがBinomial(n=12, q)で生成されている場合の事前分布がBeta(a, a)のときの期待予測誤差のプロットをaを動かすことによってアニメ化。

a=0.5のJeffreys事前分布が最大期待予測誤差最小化の意味でほぼ最適。

gist.github.com/genkuroki/efcf…

#統計

データがNegativeBinomial(k=3, q)の値+kで生成されている場合の事前分布がBeta(a, a)のときの期待予測誤差のアニメーション。

a=0.37の事前分布がこの場合には最適になっており、Jeffreys事前分布からずれています。

これはk=3が小さいことが原因。
gist.github.com/genkuroki/efcf…

#統計 Binomial(n, q)はn回の試行を行ったときの表の出る回数kの分布。

NegativeBinomial(k, q)の分布にkを足したものは、ちょうどk回表が出るまでに必要な試行回数nの分布。

データの数値が同じ n=12, k=3 であっても、実験の止め方のルールの違いによって、最適な事前分布の取り方は違う。

#統計 n, k を大きくするとどうなるか。

n=120のBinomial(n=120, q)の場合のアニメーション。

a=0.5のJefffreys事前分布が最適。

gist.github.com/genkuroki/efcf…

#統計

k=51のNegativeBinomial(k=51, q)の場合のアニメーション。

k=3ではa=0.37が最適でしたが、k=51ではa=0.5のJeffreys事前分布が最適なようです。
gist.github.com/genkuroki/efcf…

#統計 以上のアニメーションを見ると、全般的にa=0.5のBeta(0.5, 0.5)のJeffreys事前部ぷの優秀性がよく分かりますね。(注意：特異モデルではJeffreys事前分布は予測誤差を増大させる！)

二項分布の場合にnが小さい場合にはJeffreys事前分布がとてもよいと思いました。

#統計 a→0の場合が最尤法に対応しているので、最尤法は期待予測誤差を最小化したい場合には全然よろしくなさそうなこともよく分かりました。

適切に事前分布を使った方が期待予測誤差が小さくなります。

#統計 大学の講義などで「最尤法は客観的だが、事前分布を使うベイズ統計はそうではない」と聴いた人がいたとしたら、嘘八百を教わって大損こいていると思います。

適切な事前分布の使用は最もシンプルなベルヌイ分布モデルの場合にさえ予測性能を上げます。