#Julia言語 私のちょっと古めのパソコンでも、Juliaならば
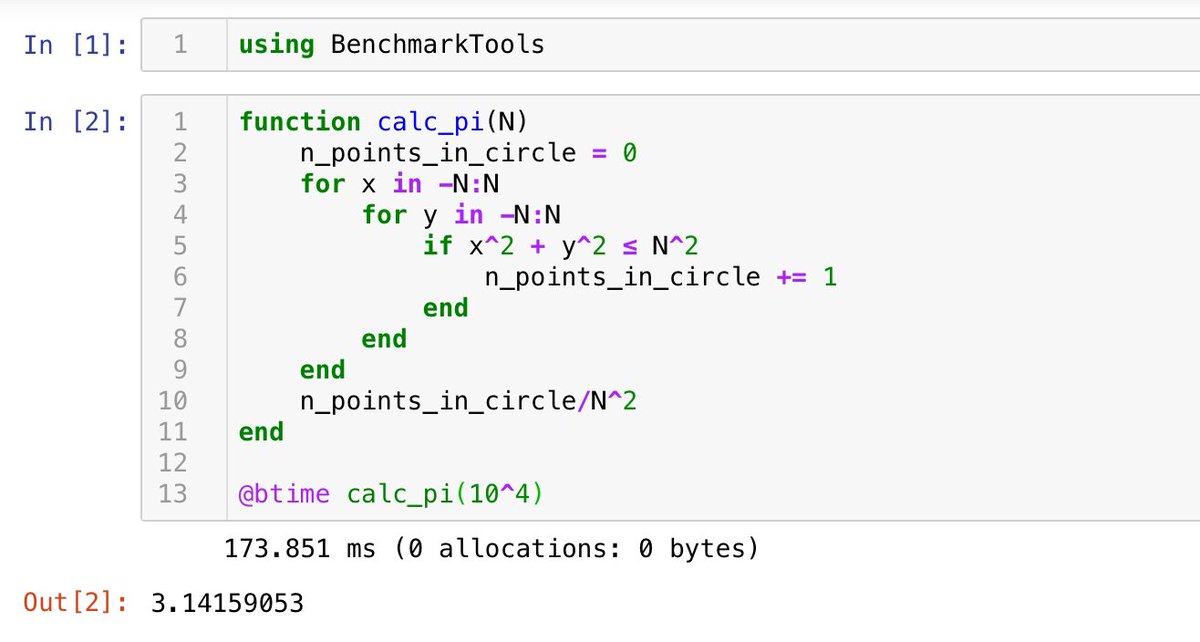
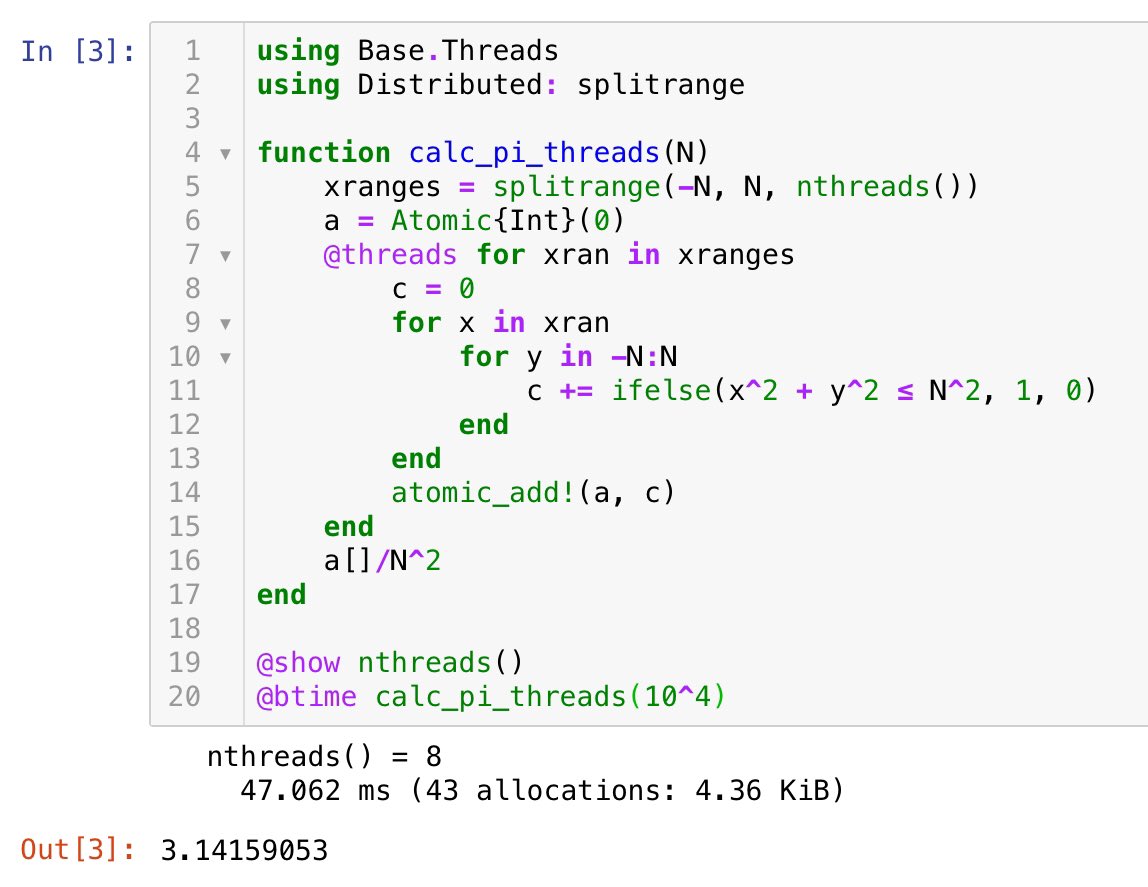
N = 10^4
シングルスレッド→ 0.174 sec
8スレッド並列→ 0.047 sec
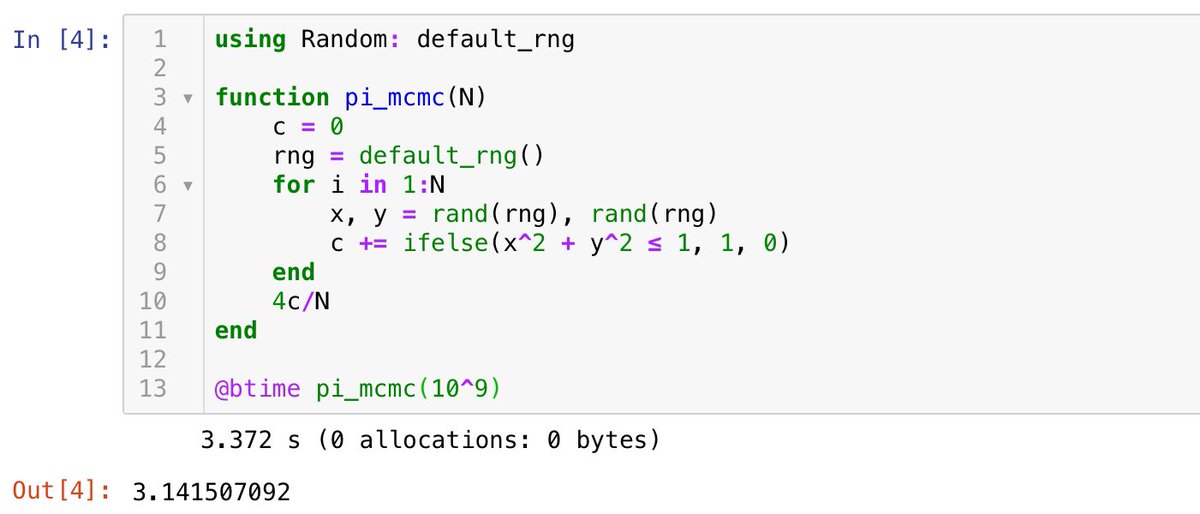
でした。よくあるπのモンテカルロ計算では
N = 10^9
シングルスレッド→ 3.4 sec
8スレッド並列→ 0.8 sec
ソースコード↓
gist.github.com/genkuroki/7f4c…



N = 10^4
シングルスレッド→ 0.174 sec
8スレッド並列→ 0.047 sec
でした。よくあるπのモンテカルロ計算では
N = 10^9
シングルスレッド→ 3.4 sec
8スレッド並列→ 0.8 sec
ソースコード↓
gist.github.com/genkuroki/7f4c…
https://twitter.com/akiraokumura/status/1339884184714629120

#Julia言語 大雑把に10^9回の単純なループに換算できる計算はすぐに終わってくれないと困る。
#Julia言語 Juliaを使っていると言語やパッケージの開発者達が気を使ってくれているおかげで大丈夫なのですが、「どのライブラリを使って計算するか」で計算速度が決まってしまう場合が結構あります。
πのモンテカルロ計算では擬似乱数発生器の質と速度が決定的に重要。選択に失敗するとはまる。
πのモンテカルロ計算では擬似乱数発生器の質と速度が決定的に重要。選択に失敗するとはまる。
#Julia言語 Isingモデルのシミュレーションでも擬似乱数発生器の選択が非常に重要です。
専門家であればどの擬似乱数発生器を選ぶのが適切かわかっているのでしょうが、私のようなど素人はそういう基本的なことを知らないので、はまってしまうことがある。
専門家であればどの擬似乱数発生器を選ぶのが適切かわかっているのでしょうが、私のようなど素人はそういう基本的なことを知らないので、はまってしまうことがある。
#Julia言語 どのライブラリのrand()を使うかでさえ非自明。
他の決まり切った計算についてもそうです。
統計でよく使われる基本特殊函数の計算速度はCやFortranで書かれた枯れたライブラリでもベストの速さから程遠い場合がある。Julia言語では誤差函数についてはJuliaで書いて解決しています。
他の決まり切った計算についてもそうです。
統計でよく使われる基本特殊函数の計算速度はCやFortranで書かれた枯れたライブラリでもベストの速さから程遠い場合がある。Julia言語では誤差函数についてはJuliaで書いて解決しています。
#Julia言語 しんどい計算をしたい人は、GPUと自動微分を両方同時に使いたくなると思うのですが、GPUにしても、自動微分にしても、専門家が書いたパッケージ経由でないとど素人は手も足も出ない感じ。
そういう専門家の助けが必要な道具を気軽に使えるかどうかも重要。
そういう専門家の助けが必要な道具を気軽に使えるかどうかも重要。
#Julia言語 1つの単純な仕事を繰り返すだけの計算によるベンチマークテストの結果を見ても、複数のツールを組み合わせて実行される実戦での性能は分からないと思う。
そういうことを押さえた上で、円周率の簡易計算の計算速度を眺めるとよいと思います。
そういうことを押さえた上で、円周率の簡易計算の計算速度を眺めるとよいと思います。
• • •
Missing some Tweet in this thread? You can try to
force a refresh