1/
Get a cup of coffee.
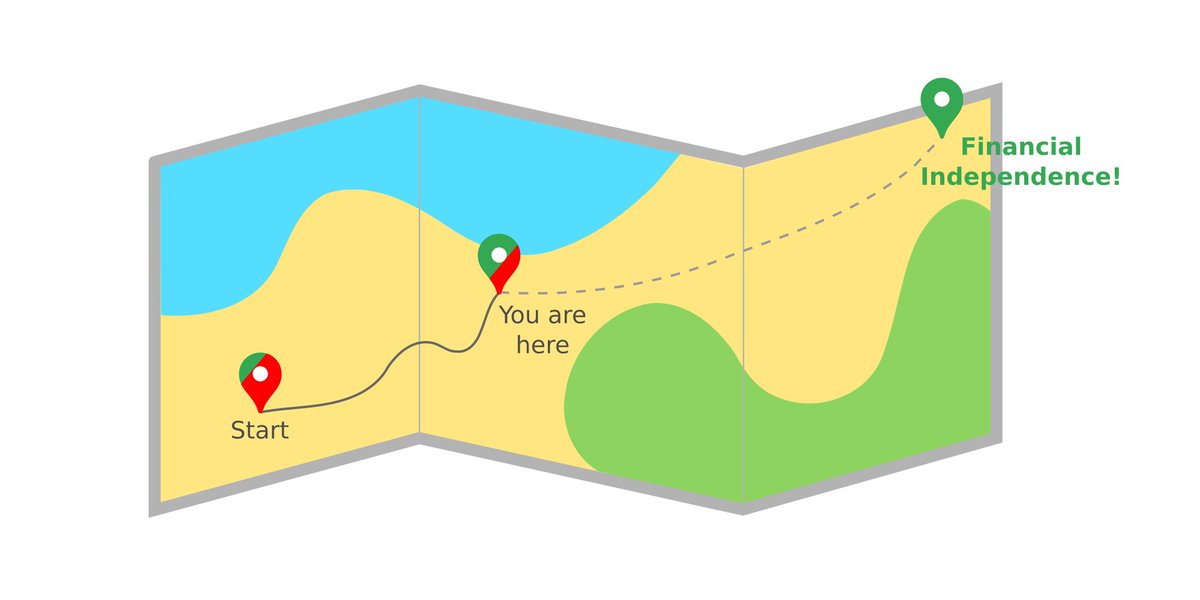
In this thread, I'd like to share with you a simple way to measure and track your progress towards financial independence.
Get a cup of coffee.
In this thread, I'd like to share with you a simple way to measure and track your progress towards financial independence.
2/
Financial independence is an end goal.
To define this goal properly, you need to answer 2 key questions.
(i) When would you consider yourself financially independent? And,
(ii) In how much time do you want to get there?
Financial independence is an end goal.
To define this goal properly, you need to answer 2 key questions.
(i) When would you consider yourself financially independent? And,
(ii) In how much time do you want to get there?
3/
Typically, financial independence means:
a) You won't have to work another day in your life for money, and
b) You and your family will still be able to live comfortably to the end of your days.
Typically, financial independence means:
a) You won't have to work another day in your life for money, and
b) You and your family will still be able to live comfortably to the end of your days.
4/
Let's say you want to reach financial independence in the next 10 years.
How much money do you need to amass by that time?
Well, suppose your family's expenses are ~$60K per year now.
If inflation runs at ~2% per year, 10 years from now, your annual expenses will be ~$75K.
Let's say you want to reach financial independence in the next 10 years.
How much money do you need to amass by that time?
Well, suppose your family's expenses are ~$60K per year now.
If inflation runs at ~2% per year, 10 years from now, your annual expenses will be ~$75K.
5/
Let's say you want your expenses to be under 3% of your portfolio at that time.
This is called the "3% Rule".
It means your portfolio's size should be about $2.5M (as 3% of $2.5M = $75K).
For more on the 3% Rule and such:
Let's say you want your expenses to be under 3% of your portfolio at that time.
This is called the "3% Rule".
It means your portfolio's size should be about $2.5M (as 3% of $2.5M = $75K).
For more on the 3% Rule and such:
https://twitter.com/10kdiver/status/1287043526153273344
6/
So that's the goal: to amass a $2.5M portfolio in the next 10 years.
Of course, this goal is personal. One size does not fit all.
For example, you may feel comfortable only with a more conservative inflation assumption -- say 4% (not 2%) per year.
So that's the goal: to amass a $2.5M portfolio in the next 10 years.
Of course, this goal is personal. One size does not fit all.
For example, you may feel comfortable only with a more conservative inflation assumption -- say 4% (not 2%) per year.
7/
Or in 10 years, you may become eligible for social security benefits.
Of the $75K you need per year, $30K may come from social security.
In this case, your portfolio needs to supply only $45K per year. By the 3% Rule, this means you only need a $1.5M portfolio.
Or in 10 years, you may become eligible for social security benefits.
Of the $75K you need per year, $30K may come from social security.
In this case, your portfolio needs to supply only $45K per year. By the 3% Rule, this means you only need a $1.5M portfolio.
8/
So, the exact goal you set will depend on your personal preferences and circumstances.
But generally, a good way to arrive at this goal is to, a) estimate the annual expenses your portfolio needs to provide for, and (b) set a reasonable withdrawal rate (like 3%).
So, the exact goal you set will depend on your personal preferences and circumstances.
But generally, a good way to arrive at this goal is to, a) estimate the annual expenses your portfolio needs to provide for, and (b) set a reasonable withdrawal rate (like 3%).
9/
For this thread, let's go with our original "$2.5M in the next 10 years" goal.
That's "Step 1" in planning for financial independence: setting an end state (eg, a $2.5M portfolio) and a time to reach it (eg, in 10 years).
For this thread, let's go with our original "$2.5M in the next 10 years" goal.
That's "Step 1" in planning for financial independence: setting an end state (eg, a $2.5M portfolio) and a time to reach it (eg, in 10 years).
10/
Step 2 is simple. It's just figuring out your current status -- how far away are you from your financial independence goal?
For example, if your current portfolio is worth $500K, you're already a fifth of your way there. You only need $2M more to reach your goal.
Step 2 is simple. It's just figuring out your current status -- how far away are you from your financial independence goal?
For example, if your current portfolio is worth $500K, you're already a fifth of your way there. You only need $2M more to reach your goal.
11/
Step 3 is the real meat: figuring out the various paths that you can take to go from your current state to your goal.
Your path to financial independence will typically involve 2 activities: Saving and Investing.
Step 3 is the real meat: figuring out the various paths that you can take to go from your current state to your goal.
Your path to financial independence will typically involve 2 activities: Saving and Investing.
12/
Let's say you save $S per year, and your portfolio grows at I% per year (S for Saving, I for Investing).
If your portfolio is now worth $500K, you need to add $2M over the next 10 years to reach your $2.5M goal.
Key idea: Several combinations of S and I can get you there.
Let's say you save $S per year, and your portfolio grows at I% per year (S for Saving, I for Investing).
If your portfolio is now worth $500K, you need to add $2M over the next 10 years to reach your $2.5M goal.
Key idea: Several combinations of S and I can get you there.
13/
At one extreme, you can rely only on Saving. No Investing.
If you're able to save $200K per year, that's $2M over 10 years. This $2M, plus the $500K you already have, gets you to your $2.5M goal -- with zero investing.
This corresponds to: S = $200K, I = 0%.
At one extreme, you can rely only on Saving. No Investing.
If you're able to save $200K per year, that's $2M over 10 years. This $2M, plus the $500K you already have, gets you to your $2.5M goal -- with zero investing.
This corresponds to: S = $200K, I = 0%.
14/
Of course, saving $200K per year is no easy task -- unless your income is super high, or you have a super profitable business or something like that.
But if you can do it, you'll be able to achieve your financial independence goal in 10 years with zero need for investing.
Of course, saving $200K per year is no easy task -- unless your income is super high, or you have a super profitable business or something like that.
But if you can do it, you'll be able to achieve your financial independence goal in 10 years with zero need for investing.
15/
At the other extreme, you can rely only on Investing. No Saving.
If you can compound your $500K portfolio at ~17.5% per year for the next 10 years, that alone takes you to your $2.5M financial independence goal. No need to save a dime more.
This is: S = $0, I = 17.5%.
At the other extreme, you can rely only on Investing. No Saving.
If you can compound your $500K portfolio at ~17.5% per year for the next 10 years, that alone takes you to your $2.5M financial independence goal. No need to save a dime more.
This is: S = $0, I = 17.5%.
16/
Of course, compounding at 17.5% per year for 10 years isn't easy either, unless you're really good at investing (or really lucky!).
But if you can do it, you'll be financially independent in 10 years -- even if you save nothing during this time.
Of course, compounding at 17.5% per year for 10 years isn't easy either, unless you're really good at investing (or really lucky!).
But if you can do it, you'll be financially independent in 10 years -- even if you save nothing during this time.
17/
Most likely, you won't be at either of these extremes.
You'll be somewhere in the middle -- relying on some *combination* of Saving and Investing to get to your goal.
The more you save, the less you need to rely on returns from investing. And vice versa.
Most likely, you won't be at either of these extremes.
You'll be somewhere in the middle -- relying on some *combination* of Saving and Investing to get to your goal.
The more you save, the less you need to rely on returns from investing. And vice versa.
18/
Here's a picture showing various combinations of S and I.
S is on the X axis. I is on the Y axis.
The red region represents failure to achieve financial independence in the time allotted.
The green region denotes success.
Here's a picture showing various combinations of S and I.
S is on the X axis. I is on the Y axis.
The red region represents failure to achieve financial independence in the time allotted.
The green region denotes success.

19/
As you can see, the higher your Savings (S), the lower the return you need from Investing (I) to cross over into the green region.
This red/green chart is a super useful tool. It helps you track and measure your progress towards financial independence.
As you can see, the higher your Savings (S), the lower the return you need from Investing (I) to cross over into the green region.
This red/green chart is a super useful tool. It helps you track and measure your progress towards financial independence.
20/
Key idea: the bigger the red region, the further away you are from financial independence.
Over time, as you make progress towards your goal, the red region will ideally shrink. The green region will expand.
Key idea: the bigger the red region, the further away you are from financial independence.
Over time, as you make progress towards your goal, the red region will ideally shrink. The green region will expand.
21/
When you finally reach financial independence, the chart will turn all green.
For example, if you already have a $3M portfolio, you need zero Saving and zero Investing. You've already achieved your $2.5M goal, and then some.
Here's how that looks:
When you finally reach financial independence, the chart will turn all green.
For example, if you already have a $3M portfolio, you need zero Saving and zero Investing. You've already achieved your $2.5M goal, and then some.
Here's how that looks:

22/
So, you can track your progress by looking at how much the red region shrinks from year to year.
For example, in Year 1, suppose you save $100K, and also get a 20% investment return.
That's progress! The red region will shrink to reflect it.
Like so:
So, you can track your progress by looking at how much the red region shrinks from year to year.
For example, in Year 1, suppose you save $100K, and also get a 20% investment return.
That's progress! The red region will shrink to reflect it.
Like so:
23/
But then, say Year 2 is a bad year for your investments. Your portfolio goes down 30%.
But you partially offset that by saving $75K.
Even so, this is a step back. The red region will expand:
But then, say Year 2 is a bad year for your investments. Your portfolio goes down 30%.
But you partially offset that by saving $75K.
Even so, this is a step back. The red region will expand:
25/
This is progress in most years. But from time to time, there's an occasional setback.
Still, it's enough to achieve the $2.5M goal -- a year ahead of schedule.
Over the years, the red/green chart evolves like this:
This is progress in most years. But from time to time, there's an occasional setback.
Still, it's enough to achieve the $2.5M goal -- a year ahead of schedule.
Over the years, the red/green chart evolves like this:
26/
So, here are the key ideas:
Key idea 1: Set a financial independence goal. For example, "to amass a $2.5M portfolio in the next 10 years".
You can arrive at this goal by making reasonable assumptions about expenses, inflation, withdrawal rates, etc.
So, here are the key ideas:
Key idea 1: Set a financial independence goal. For example, "to amass a $2.5M portfolio in the next 10 years".
You can arrive at this goal by making reasonable assumptions about expenses, inflation, withdrawal rates, etc.
27/
Key idea 2: Figure out what combinations of Saving (S) and Investing (I) will get you from your current state to your goal.
You can do this by constructing a red/green chart like the ones I showed above.
Key idea 2: Figure out what combinations of Saving (S) and Investing (I) will get you from your current state to your goal.
You can do this by constructing a red/green chart like the ones I showed above.
28/
Key idea 3: Periodically track your progress towards the goal.
Progress is measured by how much the red area shrinks from year to year.
That is, over time, the chart should become more and more green.
Key idea 3: Periodically track your progress towards the goal.
Progress is measured by how much the red area shrinks from year to year.
That is, over time, the chart should become more and more green.
29/
This means, over time, you bring down the Saving and Investing thresholds you need to meet your goal.
As these hurdles become smaller, more and more combinations of S and I will get you to your goal.
It'll become harder and harder to miss the goal.
This means, over time, you bring down the Saving and Investing thresholds you need to meet your goal.
As these hurdles become smaller, more and more combinations of S and I will get you to your goal.
It'll become harder and harder to miss the goal.
30/
Also, from time to time, you may need to modify the goal itself.
This is normal.
After all, deciding on the goal is not an exact science. And a large part of it is based on personal preferences and circumstances, which can change over time.
Also, from time to time, you may need to modify the goal itself.
This is normal.
After all, deciding on the goal is not an exact science. And a large part of it is based on personal preferences and circumstances, which can change over time.
31/
The important thing is to periodically review the goal, and change it if it no longer makes sense.
Also, if the red area is not shrinking rapidly enough from year to year, you may need to find a way to earn more, save more, or invest better.
The important thing is to periodically review the goal, and change it if it no longer makes sense.
Also, if the red area is not shrinking rapidly enough from year to year, you may need to find a way to earn more, save more, or invest better.
32/
Everything I've said in this thread is fairly simple.
At its core, financial planning is not that complicated.
If you start early, set goals, and regularly track your progress towards them, the odds are good that you'll achieve financial independence in reasonable time.
Everything I've said in this thread is fairly simple.
At its core, financial planning is not that complicated.
If you start early, set goals, and regularly track your progress towards them, the odds are good that you'll achieve financial independence in reasonable time.
33/
For example, here's a heart warming story from @morganhousel's book, The Psychology of Money.
A janitor built a net worth of over $8M -- by starting early, living below his means, saving responsibly, and investing reasonably intelligently.
For example, here's a heart warming story from @morganhousel's book, The Psychology of Money.
A janitor built a net worth of over $8M -- by starting early, living below his means, saving responsibly, and investing reasonably intelligently.

34/
In my experience, when it comes to financial planning, a lot of people struggle with inertia.
The first step is the hardest.
It's not obvious how to get started.
And once started, it's not obvious how to stay on track.
I hope this thread helps with some of that.
In my experience, when it comes to financial planning, a lot of people struggle with inertia.
The first step is the hardest.
It's not obvious how to get started.
And once started, it's not obvious how to stay on track.
I hope this thread helps with some of that.
35/
Thank you very much for reading to the end of yet another long thread!
All the best on your journey towards financial independence!
/End
Thank you very much for reading to the end of yet another long thread!
All the best on your journey towards financial independence!
/End
A1/
Several people have asked me for a step-by-step procedure to draw Red/Green charts like the ones I showed above.
Hence this appendix to the tweetstorm.
Several people have asked me for a step-by-step procedure to draw Red/Green charts like the ones I showed above.
Hence this appendix to the tweetstorm.
A2/
To draw a Red/Green chart, it's a good idea to first understand the math.
What exactly happens when you save $S every year, and put it into a portfolio that itself grows at I% every year?
Here's that math:


To draw a Red/Green chart, it's a good idea to first understand the math.
What exactly happens when you save $S every year, and put it into a portfolio that itself grows at I% every year?
Here's that math:



A3/
The math above uses a formula for the sum of a geometric sequence.
Here's a refresher on that:
The math above uses a formula for the sum of a geometric sequence.
Here's a refresher on that:
https://twitter.com/10kdiver/status/1307324413876953091
A5/
If you studied and understood the math in this appendix, you have even more determination and persistence than those who got to the end of the original thread.
Kudos!
Have a great weekend.
/End
If you studied and understood the math in this appendix, you have even more determination and persistence than those who got to the end of the original thread.
Kudos!
Have a great weekend.
/End
• • •
Missing some Tweet in this thread? You can try to
force a refresh