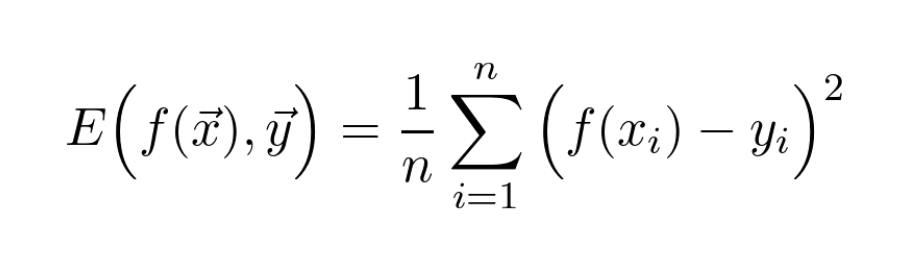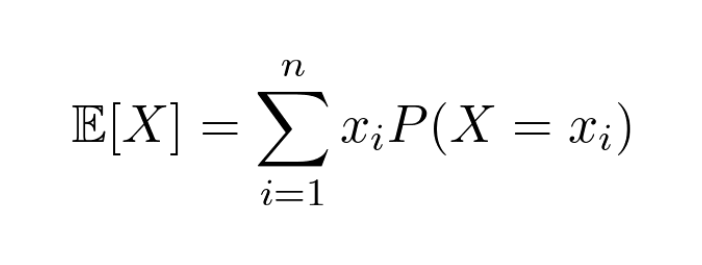Thread by @TivadarDanka

You can explain the Bayes formula in pure English.

Even without using any mathematical terminology.

Despite being overloaded with seemingly complex concepts, it conveys an important lesson about how observations change our beliefs about the world.

Let's take it apart!

Essentially, the Bayes formula describes how to update our models, given new information.

To understand why, we will look at a simple example with a twist: coin tossing with an unfair coin.

Let's suppose that we have a magical coin! It can come up with heads or tails when tossed, but not necessarily with equal probability.

The catch is, we don't know the exact probability. So, we have to perform some experiments and statistical estimation to find that out.

To mathematically formulate the problem, we denote the probability of heads with 𝑥.

What do we know about 𝑥? 🤔

At this point, nothing. It can be any number between 0 and 1.

Instead of looking at 𝑥 as a fixed number, let's think about it as an observation of the experiment 𝑋.

To model our (lack of) knowledge about 𝑋, we select the uniform distribution on [0, 1].

This is called the 𝑝𝑟𝑖𝑜𝑟, as it expresses our knowledge before the experiment.

So, suppose that we have tossed our magical coin up and it landed on tails.

How does it influence our model about the coin? 🤔

What we can tell is that if the probability of heads is some 𝑥, then the 𝑙𝑖𝑘𝑒𝑙𝑖ℎ𝑜𝑜𝑑 of our experiment resulting in tails is 1-𝑥.

Notice that we want to know the probability distribution with the condition and the event in the other way around: we are curious about our probabilistic model of the parameter, given the result of our previous experiment.

This is called the 𝑝𝑜𝑠𝑡𝑒𝑟𝑖𝑜𝑟 distribution.

Now let's put everything together!

The Bayes formula is exactly what we need, as it expresses the posterior in terms of the prior and the likelihood.

Might be surprising, but the true probability of the experiment resulting in tails is irrelevant. 🤔

Why? Because it is independent of 𝑋. Also, the integral of the posterior evaluates to 1.

Here it is 0.5, but in the general case, this can be hard to evaluate analytically.

So, we have our posterior. Notice that it is more concentrated around 𝑥 = 0. (Recall that 𝑥 is the probability of heads.)

This means that if we only saw a single coin toss and it resulted in tails, our guess is that the coin is biased towards that.

Of course, we can do more and more coin tosses, which can be used to refine the posterior even further.

(After 𝑘 heads and 𝑛 - 𝑘 tails, the posterior will be the so-called Beta distribution, more info here: en.wikipedia.org/wiki/Beta_dist…)

To summarize, here is the Bayes formula in pure English. (Well, sort of.)

posterior ∝ likelihood times prior

Or, in other words, the Bayes formula describes how to update our models, given new information

Bonus!

One of the most surprising applications of the Bayes formula is in connection with medical tests.

Check out this recent thread by @svpino!

https://twitter.com/svpino/status/1362354925548810241

More bonus!

It might be surprising, but Bayes theorem also plays a part in the definition of Mean Square Error.

I did a short explanation of this in a recent thread, you can find it here:

https://twitter.com/TivadarDanka/status/1361699203790106625