Thread by @AlanZucconi

Let's talk about NEURAL NETWORKS. 🧠

Most of you are probably familiar with them. 🧑‍💻

But not many know HOW they actually work and—even more importantly—WHY they work. 🔧

So, let's take a journey to understand what makes Neural Networks so effective... 📊

#ML #AI #NN

🧵👇

Let's start with a simple question...

❓ What problem are NNs trying to solve? 🤔

Generally speaking, NNs are trained on examples, to produce predictions based on some input values.

The example data (input + desired output) draws a curve that the NN is trying to fit.

In a nutshell, NNs are—like most ML tools—a fancy way to fit the curves inherently generated by the examples used to train it.

The more inputs it needs, and the more outputs it produces, the higher the dimension of the curve.

The simplest curve we can fit is ...a line! 😅

Fitting a line is known by Mathematicians & Statisticians as LINEAR REGRESSION. 📈

The equation of a line is:
𝐲 = 𝐱𝐰 + 𝐛

where:
🔸 𝐰: Slope
🔸 𝐛: Y-intercept

Fitting a line means finding the 𝐰 & 𝐛 of the line that best fits the input data! 🔍

To find which line better fits the training data, we need to define what "better" means first.

There are many ways to measure "linear fitness", and they all take into account how close each point is to the line.

The RMSE (Root Mean Square Error) is very popular metric.

On top of the "traditional" algebraic form (𝐲 = 𝐱𝐰 + 𝐛), let's introduce a more "visual" way to represent equations.

💡 NETWORKS allow us to better see the relationships between each part.

It will be important later, trust me! 😎

LINEAR regression, however, only work well with LINEAR data.

❓ What if out data is "binary" instead? 🤔

This is common with many decision-making problems.

For instance:
🔸 𝐱: the room temperature 🌡️
🔸 𝐲: either 0 or 1, to turn the fan ON/OFF ❄️

If we try to naively use LINEAR REGRESSION to fit binary data, we will likely get a line that passes through both sets of points.

The example below shows the "best" fitting line, according to RMSE.

It's a bad fit. ❌

❓ Can we "fix" linear interpolation? 🤔

In *this* special case, we can! 😎

Let's find a DIFFERENT line. Not the one that BEST FITS the data, but the one that BEST SEPARATES the data.

So that:

🔹 When 𝐲 ≤ 0, we return 0 (turn fan OFF 🔴)
🔹 When 𝐲 > 0, we return 1 (turn fan ON 🔵)

To do that, we need to update our MODEL:
𝐲 = 𝐬(𝐱𝐰 + 𝐛)

where 𝐬() is a the HEAVISIDE STEP function.

That will be the ACTIVATION FUNCTION of our network.
Other commonly used AFs are:
🔹 Sigmoid
🔹 Tanh
🔹 Rectified Linear Unit (ReLU)
🔹 Leaky ReLU

Ultimately, the ACTIVATION FUNCTION is where the magic happens, because it adds NON-LINEARITY to our MODEL. ✨

This gives us the power to fit virtually any type of data! 🔮

This is (more or less!) what a PERCEPTRON is: the grandfather of modern Neural Networks. 🧓

Now that we have PERCEPTRONs, let's see how we can use them as the building blocks of more complex networks.

For instance, let's imagine a more complex training data ("ternary" data? 🤔).

A perceptron can only fit 2/3 of the data.
So, why not using ...THREE of them? 😎

The FIRST perceptron fits the first 2/3 of the data:
1⃣ 🔴📈🔵 ⚫️

The SECOND perceptron fits the last 2/3 of the data:
2⃣ ⚫️ 🔵📉🔴

What's left to do now is to use a THIRD perceptron to merge the first two:
3⃣ 𝐲=(📈+📉)/2 - 0.5

This is a better view of the resulting network, with each colour indicating a different perceptron.

Pretty neat, right? 😎

Training a network like requires finding the 7 PARAMETERS so that out model fits the training data best.

Modern NNs can have MILLIONS of parameters. 🤯

If we translate that network back into its equation, you can immediately see how messy that looks.

You probably would have never come up with this yourself. But when you think in terms of curve fitting, that becomes much easier to understand.

At this point, you might wonder...

❓ What has all of this to do with the reason WHY Neural Networks are so effective? 🤔

Because we have just built an AND gate! 😎

Likewise, we can also build OR and NOT gates, de-facto proving that NNs are TURING COMPLETE! 🖥️

This proves that they can perform ANY computation that a more "traditional" computer can. 🖥️

To continue our analogy with CURVE FITTING, it means that Neural Networks have the potential to fit ANY curve in ANY number of dimensions, with as much precision as you want. 🤯

Any arbitrary 2D curve can be potentially recreated by a NN, in just three steps:

1⃣ Slice the original shape in thin sections 🔪
2⃣ Fit each section with a perceptron (AND) 📈
3⃣ Use a perceptron to merge all sections (OR) 📊

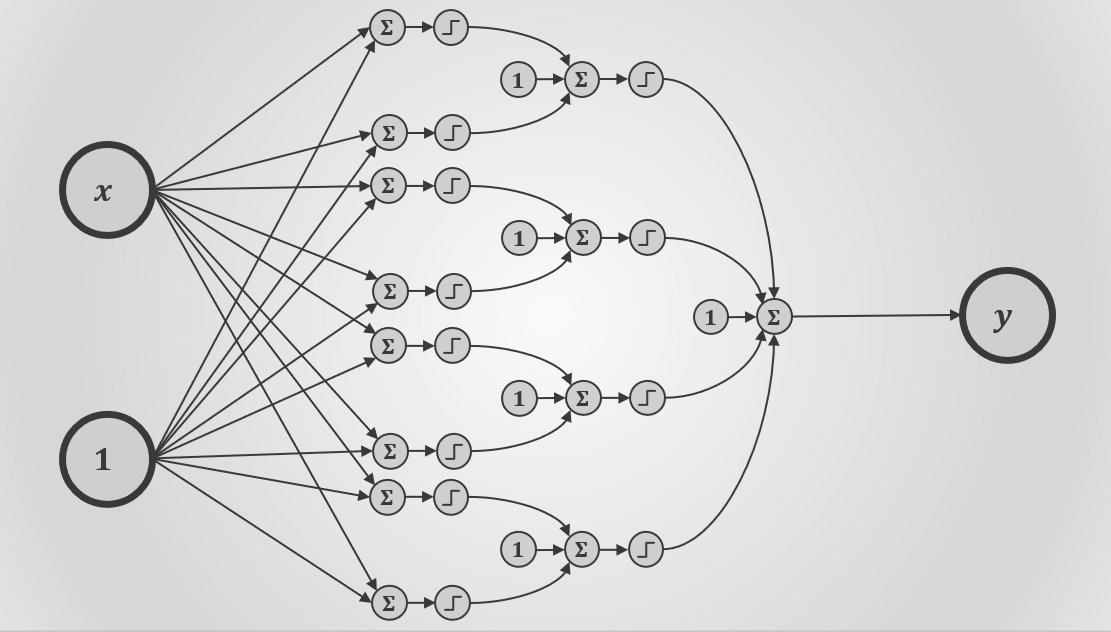
You can see here that very same principle applied to the design of a Neural Network.

This NN now has 33 parameters to fit, meaning that our search problem is now taking place in a 33-dimensional space. 🔍

That is nothing compared to the many millions some NNs nowadays have.

This is, in a nutshell, what Machine Learning is really about.

Making decisions...
...by learning from examples...
...by fitting a curve...
...by finding some numbers...
...that minimise the error of our model over a set of examples.

✨ 𝒕𝒉𝒂𝒏𝒌 𝒚𝒐𝒖 𝒇𝒐𝒓 𝒄𝒐𝒎𝒊𝒏𝒈 𝒕𝒐 𝒎𝒚 𝒕𝒆𝒅 𝒕𝒂𝒍𝒌 ✨

I tweet about Machine Learning, Artificial Intelligence, #GameDev & Shader Coding. 🧔🏻

If you are interested in any of these topics, follow me & have a look at my @Patreon! 😎

patreon.com/AlanZucconi